Methodologies 2.1 Corporate sector Corporate sector stability indicator and map The corporate sector stability indicator and map have been constructed using the following method: Data: The balance sheet data of non-government non-financial public limited companies. Frequency: Annual (1992-93 to 2011-12). From 2012-13 to 2016-17, the half-yearly balance sheet data is used for the analysis. The ratios used under each dimensions are given in the Table 1. | Table 1: Ratios used for constructing the banking stability map and the banking stability indicator | | Dimensions | Ratios | | Profitability | RoA (Gross Profit/Total Assets) #, Operating Profit/Sales #, Profit After Tax/Sales # | | Leverage | Debt/ Assets, Debt/ Equity; (Debt is taken as Total Borrowings) | | Sustainability | Interest Coverage Ratio (EBIT to interest expenses) #, interest expenses/total expenditure; | | Liquidity | Quick Assets/ Current Liabilities (quick ratio) #; | | Turn-Over | Total Sales / Total Assets #. | | # Negatively related to risk. |
The overall corporate sector stability indicator is a weighted average of 5 dimensions. The weights are obtained using PCA. The derived weights for 5 dimensions are as follows: | Profitability | Leverage | Sustainability | Liquidity | Turn-Over | | 25% | 25% | 25% | 10% | 15% | 2.2 Scheduled commercial banks Banking stability map and indicator The banking stability map and indicator present an overall assessment of changes in underlying conditions and risk factors that have a bearing on the stability of the banking sector during a period. The five composite indices used in the banking stability map and indicator represent the five dimensions of soundness, asset-quality, profitability, liquidity and efficiency. The ratios used for constructing each composite index are given in Table 2. | Table 2: Ratios used for constructing the banking stability map and the banking stability indicator | | Dimension | Ratios | | Soundness | CRAR # | Tier-I Capital to Tier-II Capital # | Leverage Ratio as Total-Assets to Capital and Reserves | | Asset- Quality | Net NPAs to Total- Advances | Gross NPAs to Total- Advances | Sub-Standard- Advances to Gross NPAs # | Restructured- Standard-Advances to Standard-Advances | | Profitability | Return on Assets # | Net Interest Margin # | Growth in Profit # | | Liquidity | Liquid-Assets to Total-Assets # | Customer-Deposits to Total-Assets # | Non-Bank-Advances to Customer-Deposits | Deposits maturing within-1-year to Total Deposits | | Efficiency | Cost to Income | Business (Credit + Deposits) to Staff Expenses # | Staff Expenses to Total Expenses | | Note: # Negatively related to risk. | Each composite index, representing a dimension of bank functioning, takes values between zero and 1. Each index is a relative measure during the sample period used for its construction, where a higher value means the risk in that dimension is high. Therefore, an increase in the value of the index in any particular dimension indicates an increase in risk in that dimension for that period as compared to other periods. For each ratio used for a dimension, a weighted average for the banking sector is derived, where the weights are the ratio of individual bank assets to total banking system assets. Each index is normalised for the sample period using the following formula: 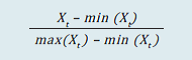 Where, Xt is the value of the ratio at time t. A composite index of each dimension is calculated as a weighted average of normalised ratios used for that dimension where the weights are based on the marks assigned for assessment for the CAMELS rating. The banking stability indicator is constructed as a simple average of these five composite indices. Estimation of losses: Expected losses, unexpected losses and expected shortfalls of SCBs The following standard definitions were used for estimating these losses: | Expected Loss (EL) | : | EL is the average credit loss that the banking system expects from its credit exposure. | | Unexpected Loss (UL) | : | UL at 100(1-α) per cent level of significance is the loss that may occur at the α-quantile of the loss distribution minus expected loss. | | Expected Shortfall (ES) | : | When the distributions of loss (Z) are continuous, expected shortfall at the 100(1- α) per cent confidence level (ESα (Z)) is defined as, ESα (Z) = E[Z | Z > VaRα (Z)] minus expected loss. Hence, Expected Shortfall is the conditional expectation of loss given that the loss is beyond the VaR level minus expected loss. |
These losses were estimated as: Loss = PD X LGD X EAD | where, EAD | = | Exposure at Default, is the total advances of the banking system. EAD includes only on-balance sheet items as PD was derived only for on-balance sheet exposures. | | LGD | = | Loss Given Default. Under the baseline scenario, the average LGD was taken as 60 per cent as per the RBI guidelines on ‘Capital Adequacy – The IRB Approach to Calculate Capital Requirement for Credit Risk’. LGD was taken at 65 per cent and 70 per cent under medium and severe macroeconomic conditions respectively. | | PD | = | Probability of Default. PD was defined as gross non-performing advances to total advances ratio. Because of unavailability of data on a number of default accounts, the size of default accounts (that is, the GNPA amount) was used for derivation of PDs. |
The losses, EL, UL and ES, were estimated by using a simulated PD distribution. As a first step an empirical distribution of the PD was estimated using the Kernel Density Estimate; second using the empirically estimated probability density function, 20,000 random numbers were drawn based on the Monte Carlo simulation and finally, EL, UL and ES were calculated by taking PDs as average PD, 99.9 per cent VaR of PD and average PD beyond 99.9 per cent loss region respectively. Macro-stress testing While multivariate regression allows evaluating the impact of select macroeconomic variables on the banking system’s GNPA and capital, the VAR model reflects the impact of the overall economic stress situation on the banks’ capital and GNPA ratios, and also takes into account the feedback effect. In these methods, the conditional mean of slippage ratio1 is estimated and it is assumed that the impact of macrovariables on credit quality will remain the same irrespective of the level of the credit quality, which may not always be true. In order to relax this assumption, quantile regression was adopted to project credit quality, wherein conditional quantile was estimated instead of the conditional mean and hence it can deal with tail risks and takes into account the non-linear impact of macroeconomic shocks. The modelling framework The following multivariate models were run to estimate the impact of macroeconomic shocks on the GNPA ratio and/or slippage ratio (SR): System level models The system level GNPAs were projected using three different but complementary econometric models: multivariate regression, VAR and quantile regression. The average of projections derived from these models was used for calculating the impact on CRAR. • Multivariate regression The analysis was carried out on the slippage ratio at the aggregate level for the commercial banking system as a whole. In order to estimate the VAR model, slippage ratio, WALR, CPI (combined) inflation, GVA at basic price growth and gross fiscal deficit-to-GDP ratio were selected. The appropriate order of VAR was selected based on minimum information criteria as well as other diagnostics and suitable order was found to be 2. Accordingly, VAR of order 2 (VAR(2)) was estimated and the stability of the model was checked based on roots of AR characteristic polynomial. The impact of various macroeconomic shocks was determined using the impulse response function of the selected VAR. • Quantile regression In order to estimate the conditional quantile of slippage ratio at 0.8, the following quantile regression was used: Bank group level models The bank groups-wise SR were projected using two different but complementary econometric models: multivariate regression and VAR. The average of projections derived from these models was used to calculate the impact on CRAR. • Multivariate regression In order to model the slippage ratio of various bank groups, the following multivariate regressions for different bank groups were used: • VAR model In order to model the slippage ratio of various bank groups, different VAR models of different orders were estimated based on the following macro variables: Public Sector Banks: GVA at basic price growth, CPI (combined)-inflation, WALR, CAB to GDP Ratio and GFD to GDP ratio of order 2. Private Sector Banks: GVA at basic price growth, real WALR and Exports to GDP ratio of order 1. Foreign Banks: CPI (combined)-inflation, WALR and CAB to GDP ratio of order 2. Sector level models Sectoral multivariate regression The impact of macroeconomic shocks on various sectors was assessed by employing multivariate regression models using the aggregate GNPA ratio for each sector separately. The dependent variables consisted of lagged GNPAs, GVA at basic price growth (aggregate or sectoral), CPI (combined)-inflation, WALR and export to GDP ratio. Estimation of GNPAs from slippages Derivation of GNPAs from slippage ratios, which were projected from the above mentioned credit risk econometric models, were based on the following assumptions: credit growth of 10 per cent; recovery rate of 3.9 per cent, 3.0 per cent, 2.2 per cent and 2.9 per cent during March, June, September and December quarters respectively; write-off rates of 5.5 per cent, 3.9 per cent, 1.8 per cent and 4.0 per cent during March, June, September and December respectively; Un-gradation rates of 3.2 per cent, 3.3 per cent, 2.6 per cent and 2.4 per cent during March, June, September and December respectively. Projection of PAT The various components of profit after tax (PAT) of banks, like, interest income, other income, operating expenses and provisions were projected using different time series econometric models (as given below). Finally, PAT was estimated using the following identity: Income Tax: The applicable income tax was taken as 35 per cent of profit before tax, which is based on the past trend of ratio of income tax to profit before tax. Impact of GNPAs on capital adequacy Finally, impact on CRAR was estimated based on the PAT estimated as mentioned in the previous section. RWA growth was assumed at 10 per cent under the baseline, 12 per cent under medium risk and 14 per cent under severe risk scenarios. Regulatory capital growth was assumed to remain at the minimum by assuming minimum mandated transfer of 25 per cent of the profit to the reserves account without considering any capital infusion by the stake holders. The projected values of the GNPAs ratio were translated into capital ratios using the ‘balance sheet approach’, under which capital in the balance sheet is affected via provisions and net profits. Single factor sensitivity analysis – Stress testing As a part of quarterly surveillance, stress tests are conducted covering credit risk, interest rate risk, liquidity risk etc. and the resilience of commercial banks in response to these shocks is studied. The analysis is done on individual SCBs as well as on the system level. Credit risk To ascertain the resilience of banks, the credit portfolio was given a shock by increasing GNPA levels for the entire portfolio as well as for few select sectors. For testing the credit concentration risk, default of the top individual borrower(s) and the largest group borrower(s) was assumed. The analysis was carried out both at the aggregate level as well as at the individual bank level. The assumed increase in GNPAs was distributed across sub-standard, doubtful and loss categories in the same proportion as prevailing in the existing stock of NPAs. However, for credit concentration risk the additional GNPAs under the assumed shocks were considered to fall into sub-standard category only. The provisioning norms used for these stress tests were based on existing average prescribed provisioning for different asset categories. The provisioning requirements were taken as 25 per cent, 75 per cent and 100 per cent for sub-standard, doubtful and loss advances respectively. These norms were applied on additional GNPAs calculated under a stress scenario. As a result of the assumed increase in GNPAs, loss of income on the additional GNPAs for one quarter was also included in total losses, in addition to the incremental provisioning requirements. The estimated provisioning requirements so derived were deducted from banks’ capital and stressed capital adequacy ratios were computed. Interest rate risk Under assumed shocks of the shifting of the INR yield curve, there could be losses on account of the fall in value of the portfolio or decline in income. These estimated losses were reduced from the banks’ capital to arrive at stressed CRAR. For interest rate risk in the trading portfolio (HFT + AFS), a duration analysis approach was considered for computing the valuation impact (portfolio losses). The portfolio losses on these investments were calculated for each time bucket based on the applied shocks. The resultant losses/gains were used to derive the impacted CRAR. In a separate exercise for interest rate shocks in the HTM portfolio, valuation losses were calculated for each time bucket on interest bearing assets using the duration approach. The valuation impact for the tests on the HTM portfolio was calculated under the assumption that the HTM portfolio would be marked-to-market. Evaluation of the impact of interest rate risk on the banking book was done through the ‘income approach’. The impact of shocks were assessed by estimating income losses on the exposure gap of rate sensitive assets and liabilities, excluding AFS and HFT portfolios, for one year only for each time bucket separately. This reflects the impact on the current year profit and loss. Liquidity risk The aim of the liquidity stress tests is to assess the ability of a bank to withstand unexpected liquidity drain without taking recourse to any outside liquidity support. Various scenarios depict different proportions (depending on the type of deposits) of unexpected deposit withdrawals on account of sudden loss of depositors’ confidence along with a demand for unutilised portion of sanctioned/committed/guaranteed credit lines (taking into account the undrawn working capital sanctioned limit, undrawn committed lines of credit and letters of credit and guarantees). The stress tests were carried out to assess banks’ ability to fulfil the additional and sudden demand for credit with the help of their liquid assets alone. Assumptions used in the liquidity stress tests are given below: • It is assumed that banks will meet stressed withdrawal of deposits or additional demand for credit through sale of liquid assets only. • The sale of investments is done with a haircut of 10 per cent on their market value. • The stress test is done under a ‘static’ mode. Stress testing the derivatives portfolios of select banks The stress testing exercise focused on the derivatives portfolios of a representative sample set of top 22 banks in terms of notional value of the derivatives portfolios. Each bank in the sample was asked to assess the impact of stress conditions on their respective derivatives portfolios. In case of domestic banks, the derivatives portfolio of both domestic and overseas operations was included. In case of foreign banks, only the domestic (Indian) position was considered for the exercise. For derivatives trade where hedge effectiveness was established it was exempted from the stress tests, while all other trades were included. The stress scenarios incorporated four sensitivity tests consisting of the spot USD/INR rate and domestic interest rates as parameters | Table 3: Shocks for sensitivity analysis | | | Domestic interest rates | | Shock 1 | Overnight | +2.5 percentage points | | Up to 1yr | +1.5 percentage points | | Above 1yr | +1.0 percentage points |
| | Domestic interest rates | | Shock 2 | Overnight | -2.5 percentage points | | Up to 1yr | -1.5 percentage points | | Above 1yr | -1.0 percentage points |
| | Exchange rates | | Shock 3 | USD/INR | +20 per cent |
| | Exchange rates | | Shock 4 | USD/INR | -20 per cent | 2.3 Scheduled urban co-operative banks Single factor sensitivity analysis – Stress testing Credit risk Stress tests on credit risk were conducted on SUCBs. The tests were based on a single factor sensitivity analysis. The impact on CRAR was studied under following four different scenarios, using the historical standard deviations (SD). • Scenario I: 1 SD shock on GNPA (classified into sub-standard advances). • Scenario II: 2 SD shock on GNPA (classified into sub-standard advances). • Scenario III: 1 SD shock on GNPA (classified into loss advances). • Scenario IV: 2 SD shock on GNPA (classified into loss advances). Liquidity risk A liquidity stress test based on a cash flow basis in the 1-28 days time bucket was also conducted, where mismatch [negative gap (cash inflow less cash outflow)] exceeding 20 per cent of outflow was considered stressful. • Scenario I: Cash outflows in the 1-28 days time bucket goes up by 50 per cent (no change in cash inflows). • Scenario II: Cash outflows in the 1-28 days time bucket goes up by 100 per cent (no change in cash inflows). 2.4 Non-banking financial companies Single factor sensitivity analysis – Stress testing Credit risk Stress tests on credit risk were conducted on non-banking financial companies (including both deposit taking and non-deposit taking and systemically important). The tests were based on a single factor sensitivity analysis. The impact on CRAR was studied under three different scenarios, based on historical SD: • Scenario I: GNPA increased by 0.5 SD from the current level. • Scenario II: GNPA increased by 1 SD from the current level. • Scenario III: GNPA increased by 3 SD from the current level. The assumed increase in GNPAs was distributed across sub-standard, doubtful and loss categories in the same proportion as prevailing in the existing stock of GNPAs. The additional provisioning requirement was adjusted from the current capital position. The stress test was conducted at individual NBFC level as well as at the aggregate level. 2.5 Interconnectedness – Network analysis Matrix algebra is at the core of the network analysis, which uses the bilateral exposures between entities in the financial sector. Each institution’s lendings to and borrowings from all other institutions in the system are plotted in a square matrix and are then mapped in a network graph. The network model uses various statistical measures to gauge the level of interconnectedness in the system. Some of the important measures are given below: Shortest path length: This gives the average number of directed links between a node and each of the other nodes in the network. Those nodes with the shortest path can be identified as hubs in the system. In-betweeness centrality: This statistic reports how the shortest path lengths pass through a particular node. Eigenvector measure of centrality: Eigenvector centrality is a measure of the importance of a node (bank) in a network. It describes how connected a node’s neighbours are and attempts to capture more than just the number of out degrees or direct ‘neighbours’ that a node has. The algorithm assigns relative centrality scores to all nodes in the network and a nodes centrality score is proportional to the sum of the centrality scores of all nodes to which it is connected. For a NxN matrix there will be N different eigen values, for which an eigenvector solution exists. Each bank has a unique eigen value, which indicates its importance in the system. This measure is used in the network analysis to establish the systemic importance of a bank and by far it is the most crucial indicator. Tiered network structures: Typically, financial networks tend to exhibit a tiered structure. A tiered structure is one where different institutions have different degrees or levels of connectivity with others in the network. In the present analysis, the most connected banks (based on their eigenvector measure of centrality) are in the innermost core. Banks are then placed in the mid-core, outer core and the periphery (the respective concentric circles around the centre in the diagrams), based on their level of relative connectivity. The range of connectivity of the banks is defined as a ratio of each bank’s in degree and out degree divided by that of the most connected bank. Banks that are ranked in the top 10 percentile of this ratio constitute the inner core. This is followed by a mid-core of banks ranked between 90 and 70 percentile and a 3rd tier of banks ranked between the 40 and 70 percentile. Banks with a connectivity ratio of less than 40 per cent are categorised as the periphery. Colour code of the network chart: The blue balls and the red balls represent net lender and net borrower banks respectively in the network chart. The colour coding of the links in the tiered network diagram represents the borrowing from different tiers in the network (for example, the green links represent borrowings from the banks in the inner core). Solvency contagion analysis The contagion analysis is in nature of stress test where the gross loss to the banking system owing to a domino effect of one or more banks failing is ascertained. We follow the round by round or sequential algorithm for simulating contagion that is now well known from Furfine (2003). Starting with a trigger bank i that fails at time 0, we denote the set of banks that go into distress at each round or iteration by Dq, q= 1,2, …For this analysis, a bank is considered to be in distress when its core CRAR goes below 6 per cent. The net receivables have been considered as loss for the receiving bank. Liquidity contagion analysis While the solvency contagion analysis assesses potential loss to the system owing to failure of a net borrower, liquidity contagion estimates potential loss to the system due to the failure of a net lender. The analysis is conducted on gross exposures between banks. The exposures include fund based and derivatives ones. The basic assumption for the analysis is that a bank will initially dip into its liquidity reserves or buffers to tide over a liquidity stress caused by the failure of a large net lender. The items considered under liquidity reserves are: (a) excess CRR balance; (b) excess SLR balance; and (c) available marginal standing facility. If a bank is able to meet the stress with liquidity buffers alone, then there is no further contagion. However, if the liquidity buffers alone are not sufficient, then a bank will call in all loans that are ‘callable’, resulting in a contagion. For the analysis only short-term assets like money lent in the call market and other very short-term loans are taken as callable. Following this, a bank may survive or may be liquidated. In this case there might be instances where a bank may survive by calling in loans, but in turn might propagate a further contagion causing other banks to come under duress. The second assumption used is that when a bank is liquidated, the funds lent by the bank are called in on a gross basis, whereas when a bank calls in a short-term loan without being liquidated, the loan is called in on a net basis (on the assumption that the counterparty is likely to first reduce its short-term lending against the same counterparty). Joint solvency-liquidity contagion analysis A bank typically has both positive net lending positions against some banks while against some other banks it might have a negative net lending position. In the event of failure of such a bank, both solvency and liquidity contagion will happen concurrently. This mechanism is explained by the following flowchart: The trigger bank is assumed to have failed for some endogenous reason, i.e., it becomes insolvent and thus impacts all its creditor banks. At the same time it starts to liquidate its assets to meet as much of its obligations as possible. This process of liquidation generates a liquidity contagion as the trigger bank starts to call back its loans. The lender/creditor banks that are well capitalised will survive the shock and will generate no further contagion. On the other hand, those lender banks whose capital falls below the threshold will trigger a fresh contagion. Similarly, the borrowers whose liquidity buffers are sufficient will be able to tide over the stress without causing further contagion. But some banks may be able to address the liquidity stress only by calling in short term assets. This process of calling in short term assets will again propagate a contagion. The contagion from both the solvency and liquidity side will stop/stabilise when the loss/shocks are fully absorbed by the system with no further failures.
|