Foreword
There is a major data gap in terms of availability of a consistent series on productivity for the Indian economy, though many individual researchers have estimated productivity for different sectors and the overall economy for specific time periods using different methodologies. In order to address this data gap, the Reserve Bank had funded a project in the Indian Council for Research on International Economic Relations (ICRIER) on productivity measurement following the EU-KLEMS (Capital, Labour, Energy, Material and Services) methodology.
The research work under the project was carried out by a team comprising Dr. Deb Kusum Das, Professor Suresh Aggarwal, Dr. Abdul Azeez Erumban, Ms Sreerupa Sengupta, Ms Kuhelika De and Shri Pilu Chandra Das under the overall guidance of Professor B. N.Goldar. The team was also guided by an Advisory Committee under the chairmanship of Professor K.L.Krishna and with Dr. Isher Ahluwalia, Prof. K.Sundaram, the late Prof. Suresh Tendulkar, Dr. Ramesh Kolli, Prof. T C Anant, Dr. R.Radhakrishna, Prof. Dale Jorgenson, Prof. Marcel Timmer, Dr. Bart Van Ark, Prof. Mary O’Mahony and the undersigned as members. The research team has since submitted three reports delineating the methodology of productivity measurement in the KLEMS framework and estimates of productivity growth along with the time series data for the period 1980-81 to 2008-09.
With the objective of making this data and methodology available to the broader community of researchers and analysts, the current Report on “Estimates of Productivity Growth for the Indian Economy” is being released by the Reserve Bank of India. The abridged version of the Report, based on the original three Reports, has been prepared by an internal team of officers led by Smt. Balbir Kaur and comprising Shri Rajib Das, Smt. Sangita Misra, Shri Alok Ghosh, Ms Alice Sebastian and Shri Anoop K. Suresh.
The Reserve Bank of India takes this opportunity to thank ICRIER and the research team for this useful endeavour, the Advisory Committee for their guidance and all those, both within the RBI and outside, who have contributed to the project in different ways. It may, however, be emphasised that the data on productivity and related analysis given in this report reflect the research output of the India KLEMS research team and, therefore, do not represent an official series on productivity by the Reserve Bank of India. Given the enormous data challenges and differences in methodology in this area, the researchers may ensure adequate caution in the use of the data.
Deepak Mohanty
Executive Director
June 10, 2014
Research Team
Research Advisor
B N Goldar
Team Members
Deb Kusum Das
Suresh Aggarwal
Abdul AzeezErumban
SreerupaSengupta
Kuhelika De
Pilu Chandra Das
Executive Summary
The Report titled “Estimates of Productivity Growth for Indian Economy” presents the work carried out by the India KLEMS project at ICRIER in collaboration with the Reserve Bank of India. The research project has computed a time series database on productivity growth for the Indian economy and has, thus, tried to fill in an important data gap in this area. Some of the distinguishing features of the project are described below:
-
It uses a detailed industrial classification consistent with the classification used in studies for the european Union (EU) and other major countries across the globe. The present report uses a 26-industry classification with six broad sectors, namely, agriculture, manufacturing, mining & quarrying, electricity, gas & water, construction and services.
-
It covers the entire Indian economy from 1980-81 (1980) to 2008-09 (2008), making it possible to analyse the sources of economic growth over a relatively long period and over the sub-periods of 1980-1999 and 2000-2008.
-
In estimating productivity growth, the quality aspects of two inputs—labour and capital —have been explicitly addressed. Also, along with the productivity estimates, the project has generated new datasets on labour, capital and the three intermediate inputs—energy, material and services—for each of the years over the time period.
-
Total Factor Productivity (TFP) growth at the industry level is computed using the gross value added and the gross output-based KLEMS framework and using growth accounting methodology. Appropriate aggregation methods have been used to compute TFP growth at the sectoral and economy levels.
-
The project relies on official data sources, such as National Accounts Statistics, employment-unemployment surveys of the National Sample Survey Organisation (NSSO), Annual Survey of Industries (ASI), and follow-up NSSO surveys on unorganised industry. For construction of the intermediate input series, namely, energy, materials and services, the input-output tables have been used.
-
In building annual time series on gross output and five inputs and factor income shares from less frequent data series, certain assumptions had to be made that call for caution in interpreting the results.
Some of the major findings of the Report are outlined below:
-
The Indian economy registered a TFP growth rate of 1.4 per cent during 1980-2008. There has been an improvement in productivity growth during 2000-2008 (2.3 per cent) over the period 1980-1999 (1.1 per cent).
-
Sector-wise, productivity growth in agriculture and the mining sector came down in the 2000s vis-à-vis the earlier period 1980-1999. In the case of construction, the steep fall in TFP growth during 1980-99 was largely arrested in the 2000s. Manufacturing, electricity and the services sector experienced an increase in the rate of TFP growth in the 2000s. Productivity growth in manufacturing was not a narrow phenomenon; rather, 8 of the 14 industries showed faster productivity growth during 2000-08.
-
Industry-wise, most high-performing industries with regard to productivity growth are from the service industries. In particular, post & telecommunications and public administration & defence make the largest TFP contributions to output growth.
As regards labour productivity, the median growth for the economy as a whole was observed to be 4.1 per cent during 1980-2008, with higher growth rates in manufacturing industries, the electricity sector and certain services.
When it comes to the growth rates of various inputs, labour input (Index of persons employed multiplied by index of labour composition) grew the fastest in construction and some service industries, while the agriculture sector remained a laggard. The growth rate of capital services in the economy was 6.5 per cent per year. It was the highest at 8.8 per cent in the broad sector of manufacturing and the lowest at 3.5 per cent in the agriculture sector. As regards the trend rates of growth for intermediate inputs, enormous heterogeneity is observed across industries in the range of 12.8 per cent (for post & telecommunication) to 2.3 per cent (for agriculture). The findings of this research project confirm the dominant role of input accumulation vis-à-vis productivity growth in explaining India’s economic growth.
Chapter 1: Introduction
Productivity Growth is studied extensively because it is a contributory factor in the improvement of living standards. In recent years, leading researchers in productivity have turned their attention to the measurement and analysis of productivity at the disaggregate industry level that covers the entire economy of selected countries. While much of the earlier research was based on a value added version of the production function, ignoring the explicit role of intermediate inputs in the production process, recent work on productivity for several countries has been based on the Gross Output version of the production function for all individual industries comprising the economies.
It is against this backdrop that the KLEMS research project was undertaken in September 2009 with two major objectives:
-
To create a database from 1980-81 onwards for estimating productivity at the disaggregated industry level for the Indian economy.
-
To estimate growth of labour productivity and total factor productivity for 26 industries and to derive estimates of productivity growth at the broad sectoral level and economy level for the period 1980-81 to 2008-09.
The KLEMS research project has computed productivity growth estimates through two different approaches: (1) using a value added production function, incorporating labour and capital inputs for the Indian economy and for 26 sectors for the period 1980-2008 and (2) gross output methodology of computing productivity and incorporating primary inputs of capital (K) and labour (L) along with the intermediate inputs of energy (E), materials (M) and services (S). In estimating productivity growth, the quality aspects of two inputs—labour and capital—have been explicitly addressed. Two dimensions of the labour input were distinguished—labour persons and educational attainment of the workforce—so that the contribution of education to value added growth at the individual industry level could be assessed. With regard to capital input, three asset types were distinguished: (i) construction (structures), (ii) transport equipment and (iii) machinery and equipment. Taking into account the differences in the length of life (depreciation) of the three asset types, measures of capital services were derived for each sector/industry. For measurement of capital input for the economy as a whole, ICT capital was also taken into account. Along with the productivity estimates, the project has also generated new datasets on labour, capital and the three intermediate inputs—energy, material and services—for each of the years over the time period that allow greater accuracy in the estimation of productivity growth at the industry level as well as the economy and its broad sectors.
The database for the study is prepared for use in the growth accounting methodology for estimating total factor productivity. Growth accounting allows a decomposition of output growth into the contribution of the different inputs and total factor productivity. The period covered is from 1980-81 (1980) to 2008-09 (2008). The industrial classification used for the study is along the lines of EU KLEMS1 so as to ensure comparability with other studies under the KLEMS project, where each economy is divided into 26 industries, as shown in Table 1.1. (In particular, the input-output (IO) tables could be aggregated to only 26 industries.)
Table 1.1:Industrial Classification for the project |
Industry No. |
Description of Industries |
1 |
Agriculture, Hunting, Forestry and Fishing |
2 |
Mining and Quarrying |
3-15 |
Manufacturing sector |
3 |
Food Products, Beverages and Tobacco |
4 |
Textiles, Textile Products, Leather and Footwear |
5 |
Wood and Products of Wood |
6 |
Pulp, Paper, Paper Products, Printing and Publishing |
7 |
Coke, Refined Petroleum Products and Nuclear Fuel |
8 |
Chemicals and Chemical Products |
9 |
Rubber and Plastic Products |
10 |
Other Non-Metallic Mineral Products |
11 |
Basic Metals and Fabricated Metal Products |
12 |
Machinery, nec |
13 |
Electrical and Optical Equipment |
14 |
Transport Equipment |
15 |
Manufacturing, nec; recycling |
16 |
Electricity, Gas and Water Supply |
17 |
Construction |
18-26 |
Service sector |
18 |
Trade |
19 |
Hotels and Restaurants |
20 |
Transport and Storage |
21 |
Post and Telecommunication |
22 |
Financial Services |
23 |
Public Administration and Defence; Compulsory Social Security |
24 |
Education |
25 |
Health and Social Work |
26 |
Other Services |
Note: Sectors highlighted in red are broad sectors under Phases I& II of KLEMS
Source: Industry level Productivity database-Phases I & II |
The industrial classification was constructed by building concordance between NIC2 2004, NIC 1998, NIC 1987 and NIC 1970 so as to ensure continuous time series from 1980 to 2008. The database for 26 industry disaggregation consists of Agricultural sector (1), Mining and Quarrying sector (1), Manufacturing industries (13), Electricity, Gas and Water supply (1), Construction (1) and Services sector (9) comprising both market and non-market services.
Measures of capital (K), labour (L), energy (E), material inputs (M) and service inputs (S) as well as gross output (GO) and value added (VA), were constructed using National Account Statistics (NAS), Annual Survey of Industries (ASI), NSSO rounds and input-output (IO) tables. For certain industries, annual data from NAS and ASI were used to compute time series on gross output. However, NSSO rounds of unregistered manufacturing, Employment and Unemployment Surveys by NSSO and input-output tables are available only for benchmark years. This necessitated interpolation and assumption of constant shares for construction of time series for gross output (unregistered manufacturing, services sector), intermediate inputs and labour inputs.
An overview of earlier productivity research in India is attempted in Chapter 2 to provide a background on both issues and methodologies that have been addressed in past studies. The Indian literature on productivity measurement is quite vast. In Chapter 3, the methodology for computing total factor productivity (as well as labour productivity) growth rates at the industry, sector and economy levels is discussed. The chapter outlines three different aggregation procedures for arriving at the economy-level productivity growth rates. The different sources used for the construction of data series and the methodology adopted for the construction of both value added and gross outputs series are explained in Chapter 4. The various sub-sections of Chapter 5 outline the methodology adopted for the construction of labour input, capital input and intermediate inputs—energy (E), material (M) and services (S). The productivity growth estimates derived using the compiled data series on gross value added, gross output, labour, capital, and Intermediate inputs are presented in Chapter 6. Chapter 7 discusses estimates of labour productivity and total factor productivity growth for six broad sectors and the economy. Chapter 8 presents a summary of the findings and conclusions derived from the study.
Chapter 2: Overview of Productivity Research in India
2.1 Introduction
The Indian literature on productivity measurement is quite vast, and is growing fast. The quality of research has improved steadily over the years. While the bulk of the past productivity research has been on the manufacturing/ industrial sector (Ahluwalia, 1985, 1991; Goldar, 1986, 2004), there have been several studies on productivity growth in agriculture and services, and the economy as a whole. The Indian productivity literature, particularly the studies on manufacturing, has been reviewed by Goldar (2011b), Goldar and Mitra (2002) and Krishna (1987, 2006, 2007), among others. This chapter presents a brief overview.
2.2 Productivity in manufacturing
Chronologically, productivity studies on Indian manufacturing can be divided into three groups. The first generation studies, which include the studies undertaken by Reddy and Rao (1962), Banerji (1975), Goldar (1986) and Ahluwalia (1985), came up with estimates of TFP growth that indicate that TFP growth in Indian manufacturing in the period 1951 to 1979 was slow or negative.
The second-generation studies drew attention to the biases in productivity estimates arising from the use of value added function and particularly the use of single deflated value added. Two prominent studies belonging to this group are Balakrishnan and Pushpangadan (1994) and Mohan Rao (1996). These studies contested the assertion made by Ahluwalia (1991) that there was a marked acceleration in TFP growth in manufacturing after 1980 which was attributed to liberalisation of economic policies. Ahluwalia had relied on the single‐deflation (SD) procedure. The more appropriate double‐deflation (DD) procedure by Balakrishnan and Pushpangadan resulted in TFPG estimates that contradicted Ahluwalia’s claim. Mohan Rao’s results based on (i) double deflation in the case of value added production function and (ii) gross output production function as well as those of Pradhan and Barik (1998) using the Gross Output function lend support to the contention of Balakrishnan and Pushpangadan that there was no turnaround in productivity growth in manufacturing in the 1980s3.
The third-generation studies have mostly focussed on the impact of industry and trade policy reforms on industrial productivity growth in the post‐reform period (i.e., the period since 1991). The third-generation studies have, in most cases, used the gross output function for the measurement of TFP. These studies take services as an input along with capital, labour, materials and energy to estimate total factor productivity growth in Indian manufacturing. The overall conclusion one may draw from the findings of these studies is that there has been no improvement in the rate of TFP growth in Indian manufacturing in the post‐reform period compared to the growth rate achieved in the 1980s. Rather, TFP growth has slowed down. Trivedi et al (2011) for instance report that the TFP growth rate in manufacturing was 1.88 per cent per annum during 1980 to 1991 and 1.05 per cent per annum during 1992 to 2007.
As regards the unorganised manufacturing sector, there have been only a couple of productivity studies. Most of them report a downward trend in TFP (Prakash (2004), Unni et al. (2001), Kathuria et al. (2010)).
2.3 Productivity in Agriculture
Estimates of TFP growth are available for aggregate agriculture, crop sector, livestock sector and even individual crops such as rice, wheat, maize and sugarcane. Estimates have also been worked out at the state level for major crops. Concerns have been expressed on the basis of available evidence that agricultural growth is becoming unsustainable as a result of resource (soil) degradation.
Mukherjee and Kuroda (2003) report that the growth rates in TFP in Indian agriculture were 1.45 per cent per annum during 1973‐80, 2.33 per cent per annum during 1981‐88 and 1.21 per cent per annum during 1989‐93. Between 1973 and 1993, the average rate of growth in TFP was 2.02 per cent per annum.
2.4 Productivity in Services
There have been several productivity studies on specific sub‐sectors of services. The Indian Railways, for example, has been studied by Sailaja (1988) and Alivelu (2006). Similarly, productivity in Indian airlines has been studied by Hashim (2003), productivity in the insurance industry by Sinha (2007), and productivity of the information technology industry by Mathur (2007).
In comparison with other sub‐sectors of services, a much larger number of studies on productivity and efficiency have been undertaken for banks, e.g., De (2004) and Sinha and Chatterjee (2008). The estimates of TFP growth presented in two studies (Goldar and Mitra 2010; Virmani, 2004) indicate that there was a marked acceleration in TFP growth in services after 1980 (Table 2.1).
Table 2.1: TFP Growth in Services, by Group |
(% per annum) |
Sub-sector/group |
Virmani (2004) |
Goldar and Mitra (2010) |
1965 to 1979 |
1980 to 1991 |
1992 to 2003 |
1960 to 1979 |
1980 to 2006 |
Trade, hotels and restaurants |
-3.0 |
1.6 |
3.6 |
-3.4 |
2.9 |
Transport, storage and communication |
1.5 |
2.8 |
4.9 |
2.0 |
3.0 |
Financing, insurance, real estate and business services |
2.4 |
4.1 |
4.7 |
2.0 |
3.9 |
Public administration and other community, social and personal services. |
|
|
|
1.1 |
3.5 |
2.5 Inter‐Sectoral Perspective
Bosworth et al. (2007) present sources of economic growth during 1960‐2004, for the three sectors, namely, agriculture, industry and services, as well as the total economy. Going by their estimates (Table 2.2) the productivity performance of the services sector was the best in the sub‐periods 1960‐80 and 1980‐2004. Overall, the performance was unsatisfactory in all three sectors during the first sub‐period.
Table 2.2: Growth of Output and TFP in Broad Sectors in 1960-2004, |
(% per annum) |
Broad Sectors/Economy |
Output Growth |
TFP Growth |
Total Economy |
1960-1980 |
3.4 |
0.2 |
1980-2004 |
5.8 |
2.0 |
Agriculture |
1960-1980 |
1.9 |
-0.1 |
1980-2004 |
2.8 |
1.1 |
Industry |
1960-1980 |
4.7 |
-0.4 |
1980-2004 |
6.4 |
1.0 |
Services |
1960-1980 |
4.9 |
0.4 |
1980-2004 |
7.6 |
2.9 |
Source: Bosworth et al. (2007). |
The estimates of productivity presented in Bosworth and Maertens (2010) show a pattern very similar to that in Bosworth et al., (2007). The growth rate of TFP in services exceeded that in industry and agriculture in the periods 1980‐90, 1990‐2000 and 2000‐2005 (Figure 2.1). The gap in the TFP growth rates between services and other sectors was relatively greater in the period 1990 to 2000. A similar pattern is observed in the estimates of TFP growth in agriculture, industry and services reported by Verma (2008).
Figure 2.1: Total factor productivity growth, India, by broad sectors of the economy
2.6 Productivity Studies for the Aggregate Economy
Four major recent studies on sources of growth of the Indian economy are by Dholakia (2002), Sivasubramonian (2004), Virmani (2004), and Bosworth, et al. (2007)4. Table 2.3 shows the estimates of TFP growth for the aggregate economy obtained in various studies. The broad conclusion one may draw from the productivity growth estimates presented in the studies is that the rate of TFP growth in the Indian economy accelerated sharply after 1980. Also, there is an indication that the rate of growth in TFP in the post‐reform period has been higher than that achieved in the 1980s. The acceleration in TFP growth at the aggregate economy level seems to be rooted in the improved productivity performance of the services sector.
Table 2.3: Estimates of TFP Growth in the Indian Economy |
Author (s) |
Method |
Period |
Estimated TFP growth
rate (% per annum) |
Dholakia (2002) |
Value added function (land included as an input) |
1960-1985
1985-2000 |
0.8
2.9 |
Sivasubramonian (2004) |
Value added function (land included as an input); estimates for non-residential sector |
1950-1960
1960-1970
1970-1980
1980-1990
1990-1999
1950-1999 |
1.8
1.2
0.2
2.0
2.0
1.4 |
Virmani (2004) |
Value added function |
1950-1964
1965-1979
1980-1991
1992-2003 |
1.9
0.1
2.5
3.6 |
Jorgenson and Vu (2005) |
Value added function (contribution of ICT investment taken into account) |
1989-1995
1995-2003 |
2.1
2.5 |
Bosworth, Collins and Virmani (2007) |
Value added function (land included as an input) |
1960-1980
1980-2004
1983-1993
1993-1999
1999-2004 |
0.2
2.0
1.7
2.8
2.0 |
Bosworth and Collins (2008) |
Value added function (land included as an input) |
1978-1993
1993-2004
1978-2004 |
1.1
2.3
1.6 |
Bosworth and Maertens (2010) |
Value added function (land included as an input) |
1980-1990
1990-2000
2000-2005 |
2.2
1.8
2.1 |
2.7 Attempted Improvements in the Present Study
The present study attempts to improve on the past productivity research in India on several counts. While the majority of the previous studies were concerned with a sector or a sub-sector of the economy, the present study has comprehensive coverage. Arguably, studies undertaken by Virmani (2004) and Bosworth et al. (2007) also have comprehensive coverage, but they have not divided the economy into as many sub-sectors or industries as done here. The second advantage of the present study is that the industrial classification and the methods of measurement of output and inputs have been chosen so as to render international comparability of the productivity estimates. This will make it possible to validate international comparisons of productivity growth for a large number of sub-sectors or industries in India. In this regard, several earlier studies have a handicap. The third point is that careful attention is paid in this study to the measurement of inputs, labour and capital. The measure of labour input takes into account the educational characteristics of the workforce. While some earlier studies have also taken into account changes in labour quality, this has by and large been ignored in the past productivity research in India. As regards capital input, an attempt is made to estimate capital service rather than use capital stock as all earlier studies in India have done. The measurement of capital services is done by taking into account the changing composition of capital assets and also the growing use of information and communication technology (ICT) in the Indian economy. This greatly improves the measurement of capital input and helps obtain a more accurate measure of total factor productivity growth.
Chapter 3: Methodology of Productivity Measurement in the KLEMS Framework:
Industry Level, Sector Level and Economy Level
3.1 Introduction
This chapter deals with the methodology for measurement of total factor productivity (TFP) growth for individual industries in the KLEMS framework and the aggregation from industry-level productivity measures to measures for broad sectors and the economy as a whole. The methodology for analysis of sources of gross output growth at the individual industry level and sources of GVA (Gross Value Added) or GDP growth at the broad sector level and economy level will also be presented in this chapter, which supplements the discussion on these aspects in Chapters 6 and 7.
3.2 Measuring Productivity Growth for Individual Industries
The methodology developed by Jorgenson and his associates and presented in Jorgenson et al. (2005) is adopted. This methodology has been followed recently in Timmer et al. (2010) for the European Union and the US.
Let the production function for industry j be denoted by
where Y is industry gross output, K is capital input, L is labour input, E is energy input, M is material input and S is services input, and T is an indicator of technology, all for industry j. All variables vary over time t, but the t subscript is not shown explicitly, for the sake of simplicity.
For the calculation of total factor productivity (TFP) growth, the accounting identity for each industry is taken into account:
The identity states that the value of gross output of industry j equals the sum of the values of the five inputs.PY denotes the price of output, PK,PL,PE,PM and PS are the prices of capital, labour, energy, material and services, respectively.
The identity implies constant returns to scale. Assuming that the five input markets are competitive and factors are paid their marginal products, gross output TFP growth AjY for industry j can be obtained as:
The sources of labour productivity growth are change in capital intensity, change in labour composition and TFP growth, as shown in (3.18).
3.3 The Industry Origins of Aggregate Grow
To use measures of individual industries to arrive at aggregate measures for broad sectors and the economy, Jorgenson et al. (2005) consider three alternative approaches to aggregation.
Approach I is based on the existence of the aggregate production function, for which four key assumptions are necessary. These assumptions are very restrictive and unrealistic. In this approach aggregate value added is simply the sum of value added for the constituent industries.
Approach II is based on the existence of the Aggregate Production Possibility Frontier. The most restrictive assumption of production function being the same for all industries is relaxed.
Aggregate value added is given by the Tornqvist formula:
PjV being the price of value added for the jth industry. Aggregate capital input and labour input are also given by the Tornqvist formula.
Approach II is preferred to Approach I.
Approach III: Direct Aggregation across Industries
This method was developed by Jorgenson, Gollop and Fraumeni (1987). Jorgenson et al. (2005) and Timmer et al. (2010) have applied this approach in their respective studies.
Labour Productivity (δ) is defined as value added per person employed, i.e., Z/N. As shown by Stiroh (2002), aggregate labour productivity can be decomposed into industry contributions as follows:
This formula enables us to determine the contribution of capital deepening, labour composition and TFP growth from each industry to aggregate labour productivity growth.
The decomposition of the growth of gross output of industry j is given by
where Xj refers to intermediate inputs
Chapter 4: Database for Gross Value Added and Gross Output
4.1 Introduction
This chapter describes the procedures used to construct the database for gross output and value added series at the industry level over the period 1980-81 (1980) to 2008-09 (2008). Both the raw data sources and the adjustments that have been made to generate the comprehensive time series on output and value added are consistent with the official National Accounts. Multiple sources of information are used for the construction of the database on gross output and gross value added. The main sources of data are the National Accounts Statistics (NAS), Input-Output transaction tables (IOTT), Annual Survey of Industries (ASI) and the follow-up surveys of unorganised manufacturing conducted by the NSSO, Office of the Economic Adviser, Ministry of Commerce and Industry. The details of the construction of various variables from these data sources are discussed in different sections of the chapter.
This chapter is divided into two sections. Section 4.2 documents the data sources and methodology for constructing the Gross Value added (GVA) series. Similarly, Section 4.3 describes the data sources and methodological details for estimating the Gross Value of Output (GVO) series. It also presents the trend growth rates and value added shares of GVA for the study period 1980 to 2008 and the empirical estimates (trend growth rates at industry level) of the GVO series for the period under study.
4.2 Gross Value Added: Data Sources and Methodology
Gross value added of a sector is defined as the value of output less the value of its intermediate inputs. Value added created by a sector is shared between labour compensation and capital compensation. The growth rates of gross value added for the total economy determines the rate at which the Indian economy is growing. The trend growth rates of gross value added in different industries determines the pace at which that industry is growing relative to the total economy.
4.2.1 Data Sources for Gross Value Added
The National Accounts Statistics (NAS) brought out by the CSO is the basic source of data on gross value added in India. NAS has provided estimates of GDP (i.e., gross value added) by industry of use at both current and constant (1999-2000) prices since 1950 at both aggregate and disaggregated levels. The sectors for which data are provided in NAS are Agriculture, Forestry & logging, Fishing, mining & quarrying, Manufacturing (registered and unregistered), Electricity, Construction, Trade, Hotels & Restaurants, Railways, Transport by other means, Storage, Communication, Banking & insurance, Real estate, Ownership of dwelling & business services, Pubic administration & defence and Other services. Further, NAS provides estimates of GDP at the disaggregated level for these industries. The data on GDP for the manufacturing sector at the more disaggregated levels are available in the ASI and NSSO quinquennial surveys for registered and unregistered manufacturing industries, respectively. These data sources are used to construct value added series for 26 industries for the period 1980 to 2008. It is to be noted that gross value added at current and constant prices has been constructed using the NAS back series, i.e., NAS 2009 and NAS 2011. The new data from NAS 2011 (2004-05 base) is linked with the old NAS 2009 data (1999-2000 base) through splicing to update the estimates for the period 2004 to 2008. Growth rates of the old series (1999-2000 base) are applied to the level of the new series (2004-05 base) with 2004-05 as the link year.
4.2.2 Methodology for Construction of Gross Value added Series
The concordance of NAS sectors and 26 industries was identified, as the first step for construction of the value added series. In India, output is adjusted for Financial Intermediation Services Indirectly Measured (FISIM). The value of such services forms a part of the income originating in the banking and insurance sector and is deducted from the GVA. The NAS provides output net of FISIM for some industry groups at the aggregate level. For instance, in the estimates of GVA obtained for the registered manufacturing sector, adjustment for FISIM in NAS is made only at the aggregate level in the absence of adequate details at a disaggregated level. However, FISIM have been allocated to all the manufacturing sectors by redistributing total FISIM across sectors proportional to their sectoral GDP shares. Similar redistribution of FISIM has been done for the trade sector and the other services sector.
For manufacturing industries where direct estimates of GVA are not available from NAS, estimates have been made using additional information from ASI and NSSO unorganised manufacturing sector data. To obtain the estimates of GVA for registered manufacturing industries, data from the ASI based on the National Industrial Classification 1998 (NIC-1998) obtained from the Economic and Political Weekly electronic database have been used. For the unregistered manufacturing sector, results from five rounds of NSSO surveys—40th round (1983-84), 45th round (1989-90), 51st round (1994-95), 56th round (2000-01) and 62nd round (2005-06)— have been used to obtain value added estimates. In India, the estimates of GVA for the unregistered manufacturing sector are obtained as a product of the work force and the corresponding GVA per worker. Information about employment in the unorganised sector is only available in the benchmark years for which NSSO survey data are available. Therefore, there is no consistent source of employment data for the years between these quinquennial surveys. The information on value added per worker is equally limited, since the value added data are updated at approximate 5-year intervals (for details, see CSO, 2007). Therefore, estimates of value added for the unregistered manufacturing sectors for the years between the benchmarks have been obtained by interpolation as well as by extrapolation.
For 19 of the 26 industries listed in Table 4.1, GVA series both at current and constant prices are directly available in NAS. GVA data series at current prices for the remaining 7 study manufacturing industries are constructed by splitting the data of 7 NAS industries using additional information from ASI and four NSSO surveys.
Once the nominal estimates of GVA of 7 manufacturing industries are obtained, the current price estimates are deflated using suitable WPI deflators to arrive at constant price series. To maintain consistency with NAS, the study has proportionately adjusted the deflated figures of 7 manufacturing industries with overall estimates of GVO of 7 NAS manufacturing industries.
It is worth noting that our aggregate estimate of GVA in manufacturing (formed from using the shares of ASI data and NSS unorganised manufacturing surveys) is consistent with the overall estimate of gross value added in NAS. As mentioned earlier, the current and constant price series of the remaining industries are directly taken from NAS.
4.2.3 Value Added Shares
One of the most interesting features of the Indian economy since the 1980s is the emergence of services as the dominant sector and as the main driver of GDP growth. Looking at the percentage distribution of value added share, it is evident that the services sector had the highest share in all three years. Among the 9 services sectors, trade, other services, transport & storage, public administration & defence and financial services had high value added shares in all three years. For the manufacturing sector, there is a slight fall in value added share from 1980 to 2008. Though agriculture has been the second largest contributor (after the services sector) to India’s GDP over the years, its share has sharply declined from 36 per cent in 1980 to 18 per cent in 2008. The share of value added of construction increased sharply from 4.6 per cent in 1980 to 8.1 per cent in 2008, while that of the services sector increased from 40 per cent in 1980 to 54 per cent in 2008.
4.2.4 Trend Growth Rate of Real Gross Value Added for 26 sectors of the Indian economy
The individual trend gross value added growth for 26 industries for the period 1980-2008 have been estimated using the exponential model for growth estimation. Table 4.1 also documents the trend GVA growth of 26 industries during the period covered.
Table 4.1: Gross value added Shares and Trend Growth Rates of Real Value Added |
Industry No. |
Industry Description |
1980 |
1995 |
2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
Gross value added Shares (in per cent) |
Growth rate in real value
added (per cent per annum) |
1 |
Agriculture, Hunting, Forestry & Fishing |
35.68 |
26.49 |
17.91 |
3.08 |
2.61 |
2.96 |
2 |
Mining & Quarrying |
1.75 |
2.35 |
2.70 |
5.90 |
3.49 |
5.30 |
3 |
Food products, Beverages & Tobacco |
2.21 |
2.12 |
2.12 |
5.45 |
6.35 |
5.68 |
4 |
Textiles & Leather products |
3.78 |
2.86 |
1.68 |
5.03 |
6.07 |
5.29 |
5 |
Wood & products |
0.95 |
0.51 |
0.22 |
1.95 |
-1.81 |
-1.91 |
6 |
Pulp, Paper and products, Printing & Publishing |
0.55 |
0.68 |
0.41 |
4.98 |
5.35 |
5.07 |
7 |
Coke, Refined petroleum products & Nuclear fuel |
0.26 |
0.58 |
1.16 |
8.32 |
6.48 |
7.86 |
8 |
Chemicals & products |
1.52 |
2.49 |
2.57 |
9.04 |
7.74 |
8.72 |
9 |
Rubber & Plastic products |
0.45 |
0.53 |
0.55 |
8.19 |
6.82 |
7.84 |
10 |
Other Non-metallic mineral products |
0.70 |
0.96 |
0.98 |
6.98 |
6.95 |
6.97 |
11 |
Basic metals and Fabricated metal products |
2.09 |
2.62 |
2.40 |
5.75 |
9.48 |
6.68 |
12 |
Machinery, nec. |
1.28 |
1.18 |
0.92 |
3.15 |
6.06 |
3.88 |
13 |
Electrical & Optical equipment |
1.09 |
1.34 |
1.55 |
6.82 |
10.70 |
7.80 |
14 |
Transport equipment |
0.85 |
1.16 |
0.74 |
6.27 |
9.63 |
7.11 |
15 |
Manufacturing, nec |
1.04 |
0.85 |
0.76 |
7.59 |
4.93 |
6.92 |
16 |
Electricity, Gas & Water Supply |
1.64 |
2.70 |
1.57 |
7.59 |
4.70 |
6.86 |
17 |
Construction |
4.57 |
4.90 |
8.13 |
4.70 |
9.99 |
6.03 |
18 |
Trade |
10.81 |
12.79 |
15.37 |
6.36 |
9.04 |
7.04 |
19 |
Hotels & Restaurants |
0.79 |
1.06 |
1.50 |
7.64 |
10.85 |
8.44 |
20 |
Transport & Storage |
3.87 |
5.41 |
6.28 |
5.81 |
8.40 |
6.46 |
21 |
Post & Telecommunications |
0.60 |
1.45 |
1.60 |
9.92 |
25.86 |
13.93 |
22 |
Financial services |
3.04 |
5.49 |
5.72 |
9.70 |
9.33 |
9.61 |
23 |
Public administrative & Defence |
5.27 |
5.55 |
5.96 |
5.80 |
5.13 |
5.63 |
24 |
Education |
2.48 |
3.03 |
3.53 |
7.17 |
7.57 |
7.27 |
25 |
Health & Social work |
1.02 |
1.30 |
1.56 |
7.48 |
8.33 |
7.69 |
26 |
Other services |
11.71 |
9.61 |
12.12 |
6.04 |
7.28 |
6.35 |
|
Industry Mean |
|
|
|
6.26 |
7.59 |
6.60 |
|
Industry Median |
|
|
|
6.32 |
7.12 |
6.89 |
4.3 Gross Output: Data Sources, Methodology and Estimates
The gross output of an industry is defined as the value of production using primary factors such as labour, capital and intermediate inputs purchased from other industries. As per the growth accounting methodology, the gross output of each industry is a function of capital, labour, intermediate inputs and technology. An important advantage of gross output approach is that it provides a complete measure of production and treats all inputs—labour, capital and intermediate inputs—symmetrically. In contrast, the value added measure of output does not explicitly account for the flow of intermediate inputs that may be the primary component of an industry’s output.
4.3.1 Data Sources for Gross Output
NAS, published by the CSO, is the basic source of data used to construct the gross output series of various sectors at current and constant prices. For industries where NAS does not provide direct estimates of output, additional information is used from the ASI for registered manufacturing sectors, NSSO quinquennial surveys for unregistered manufacturing sectors, and input-output transaction tables for service sectors. As in the value added case, the required splicing is done to get a comparable time series.
4.3.2 Methodology for Construction of Gross Output Series
i) Current Price series
Concordance between NAS industries and our 26 study industries is the first step in the construction of the output series. NAS provides nominal GVO series for a) crops and plantation, b) animal husbandry, c) forestry and logging and d) fishing. By aggregating the GVO of these four sub-sectors, the output of the agriculture sector is derived.
For manufacturing industries, time series on gross output is obtained by adding the magnitudes for registered and unregistered segments of manufacturing. As mentioned earlier, NAS estimates of gross output for manufacturing industries are at a more aggregate level. In such cases, the aggregate output of NAS at current prices has been split using additional information from ASI and NSSO unorganised sector reports. Gross output data both at current and constant prices for 6 of the 13 manufacturing industries are directly picked up from NAS.
For the remaining 7 industries, output is constructed by splitting the NAS output data using ASI or NSSO distributions.ASI data (annual) has been used for registered manufacturing, whereas interpolated ratios from the NSSO 56th round (2000-01) and 62nd (2005-06) round have been used for the unregistered manufacturing sector.
For the period prior to 1999, separate output estimates for the unregistered manufacturing sector are not available in NAS. Thus, to derive the output estimates for the time period 1980 to 1998, GVA to GVO ratios are computed from NSSO survey reports of the 40th round (1984-85), 45th round (1989-90) and 51st round (1994-95). The GVA to GVO ratio for the year 1999 is directly picked up from NAS. The ratios obtained are then linearly interpolated between intermediate years and applied to time series of GVA from NAS at current prices to obtain the output estimates at current prices. The ratios of the NSSO 40th round are taken backwards to derive output numbers for the period 1980 to 1983.
Gross output series for services sectors and electricity, gas & water supply have been constructed using information from the IOTT of the Indian economy published by the CSO. The GVO to GVA ratios for services sectors are obtained from IOTT benchmark years of 1978-79, 1983-84, 1989-90, 1993-94, 1998-99 and 2003-04. These ratios are linearly interpolated for the intervening years and applied to the GVA series of NAS to derive output estimates consistent with NAS at current prices. It is to be noted that for the government-owned sector ‘Public administration & defence’ no intermediate inputs are given in the IOTT. Consequently, the value added to output ratio from the System of National Accounts tables have been applied to nominal GVA figures of NAS to estimate the output for this sector. Thus, a time series of gross output is constructed for 26 sectors at current prices.
ii) Constant Price series
Gross output series at constant prices for Agriculture, hunting, forestry & fishing, Mining & quarrying and Construction are directly available from NAS. For 6 of the 13 manufacturing industries, real GVO is taken from NAS. To arrive at constant price series for the remaining 7 industries, the study has deflated the nominal estimates with suitable WPI deflators. To maintain consistency with NAS, the study has proportionately adjusted the deflated figures with overall estimates of real GVO of 7 NAS manufacturing industries. Thus, our estimates of real GVO of total manufacturing exactly matches with NAS.
For services and electricity, gas & water supply, the nominal estimates are deflated with implicit GVA deflators from NAS to arrive at constant price series.
4.3.3 Trend Growth Rate of Real Gross Output for 26 Industries of the Indian Economy
The trend growth rate of gross output for each industry for the period 1980 to 2008 is estimated using the exponential model for growth rate estimation. Table 4.2 presents the trend growth rates of gross output of 26 KLEMS industries. For all 26 industries, the median growth rate of output was 6.9 per cent per annum. Output growth is found to be most rapid in post & telecommunications (14.2 per cent). Of the five fastest growing industries, two are producers of services (post & telecommunications and financial services) and three are manufacturing sectors (electrical & optical equipment, manufacturing nec, rubber & plastic products).All these industries posted growth rates in excess of 9.4 per cent during the period 1980 to 2008.
The study also examines the trend growth rates of gross output and value added both at the aggregate and disaggregate levels of the economy for the period 1980 to 2008. It is observed that there is a strong positive correlation between real growth of output and real growth of value added.
It is useful to highlight certain data issues related to measurement of output that are analogous to those explained in Jorgenson et al. (2005, Chapter 4) for the US economy and Timmeret al. (2010, Chapter 3) for the EU economy. The first basic measurement issue is that the annual GDP data are not consistent with the benchmark input-output tables from the official NAS. Second, there is a limitation in the estimation of gross output of electricity, since electricity produced for own use (both industries and households)/ captive power is not reported explicitly in the system of official statistics, whether ASI or other businesses. Third, the National Accounts does not provide any estimates of gross output of the services sector and, hence, the study relies on input-output transaction tables that are available at intervals of five years. This necessitates interpolation and assumption of constant shares for measuring output of services. This issue is analogous to that explained in Timmer et al. (2010) for the EU economy. Griliches (1994) paid particular attention to services sector output as a key source of uncertainty. Triplett and Bosworth (2004, 2008), in particular, concluded that in the US, output measurement in services has improved considerably, even as numerous areas for improvement still exist.
Table 4.2: Trend Growth Rate of Real Gross Output |
(per cent per annum) |
Industry No. |
Industry description |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
2.9 |
2.59 |
2.82 |
2 |
Mining & Quarrying |
5.64 |
3.4 |
5.08 |
3 |
Food products, Beverages & Tobacco |
5.74 |
8.31 |
6.38 |
4 |
Textiles & Leather products |
6.28 |
6.96 |
6.45 |
5 |
Wood & products |
–0.55 |
–2.69 |
–1.09 |
6 |
Pulp, Paper & products, Printing & Publishing |
5.82 |
5.43 |
5.72 |
7 |
Coke, Refined Petroleum products & Nuclear fuel |
4.85 |
7.13 |
5.42 |
8 |
Chemicals & Chemical products |
8.06 |
8.06 |
8.06 |
9 |
Rubber & Plastic products |
10.18 |
7.26 |
9.45 |
10 |
Other Non-metallic mineral products |
7.97 |
6.74 |
7.66 |
11 |
Basic Metals & Fabricated Metal products |
6.17 |
11.73 |
7.56 |
12 |
Machinery, nec. |
4.64 |
3.22 |
4.28 |
13 |
Electrical & optical equipment |
11.25 |
14.97 |
12.18 |
14 |
Transport equipment |
8.26 |
6.67 |
7.86 |
15 |
Manufacturing, nec |
10.33 |
8.01 |
9.75 |
16 |
Electricity, Gas & Water Supply |
8.23 |
4.85 |
7.38 |
17 |
Construction |
4.82 |
12.21 |
6.68 |
18 |
Trade |
5.4 |
8.67 |
6.22 |
19 |
Hotels & Restaurants |
6.78 |
11.21 |
7.89 |
20 |
Transport & Storage |
6.62 |
9.1 |
7.25 |
21 |
Post & Telecommunications |
9.96 |
26.67 |
14.16 |
22 |
Financial services |
9.87 |
9.87 |
9.87 |
23 |
Public administration & Defence |
5.78 |
4.95 |
5.57 |
24 |
Education |
6.83 |
7.59 |
7.02 |
25 |
Health & Social work |
4.23 |
7.05 |
4.94 |
26 |
Other services |
6.4 |
7.39 |
6.65 |
|
Industry Mean |
6.63 |
7.98 |
6.97 |
|
Industry Median |
6.34 |
7.33 |
6.85 |
Source: Authors’ calculations. |
Chapter 5: Methodology and Database for Labour, Capital and Intermediate Inputs
5.1 Introduction
Multiple sources of information have been used for the construction of the database on labour input, capital input and intermediate inputs- energy, material and services. The main sources of data are the National Accounts Statistics (NAS), Employment-Unemployment Surveys (EUS) conducted by the NSSO, Input-Output (IO) tables, Annual Survey of Industries (ASI), the follow-up surveys of unorganised manufacturing conducted by the NSSO, and PROWESS data. These published data sources are supplemented by data especially furnished by the CSO for the project.
5.2 Labour Input – Data Sources, Methodology and Estimates
Labour input is measured by combining data on labour persons and data on education. In the KLEMS framework it is desirable to estimate changes in labour composition by industries on the basis of age, gender and education. The measurement of labour composition is an attempt to distinguish one labour type from another, taking into account the embodied human capital in each person. The source of human capital could be through investment in education, experience, training, etc. The contribution to output by each person also comes from this embodied capital, and the reward (wages and earnings) to each person also includes the reward for investment in human capital. Therefore, it is essential to separate these differences in labour to clearly understand the underlying differences in labour characteristics. It is in this context that an endeavour has been made to estimate the labour composition index. However, given the limitations of India’s employment statistics, especially the non-availability of information on wages/ earnings of different categories of workers that could be used as an indication of differences in their ability, it is difficult to quantify these changes in the labour force in a pertinent way. The problems of employment statistics in India have been widely discussed in the literature (Himanshu, 2011; Sivasubramonian, 2004). This study aims to build a time series of employment data for 26 industrial sectors. However, there is no time-series data on the Indian economy, except for the organised segment. Therefore, it was essential to make certain assumptions regarding the annual changes in the employment series using the available information.
5.2.1 Data Sources and Methodology
The section develops and implements the methodology of estimating labour input incorporating the indices of labour composition.
Sources of data
The Employment and Unemployment Surveys (EUS) by the National Sample Survey Office (NSSO) is the main source for estimating the total workforce in the country by industry group, as per the National Industrial Classification (NIC). The estimates obtained from the EUS are adjusted for population. The source of data for the population is the Census of India (different years), which only gives the decadal census; so, interpolated population is used for the intervening years.
The study has used the unit-level data provided in the 38th (1983), 43rd (1987-88), 50th (1993-94), 55th (1999-2000), 61st (2004-05) and 66th (2009-10) major or quinquennial rounds of EUS that have been conducted by the NSSO since 1980. The 32nd major round (1977-78) has been used for extrapolating the labour series to 1980-81.
In the EUS, the persons employed are classified on the basis of their activity status into usual principal status (UPS), usual principal and subsidiary status (UPSS), current weekly status (CWS) and current daily status (CDS) for quinquennial rounds. UPSS is the most liberal and widely used of these concepts and despite the fact that the UPSS has some limitations5, this seems to be the best measure to use given the data.
Methodology
a) Measuring persons employed at the Industry Level
Efforts are made in this chapter to estimate persons employed industry-wise and adjust that measure for changes in labour skill by calculating the labour composition index, thus obtaining the composition corrected labour input.
Since the NSSO used the NIC 1970 to classify persons employed by industry in the 38th and 43rd rounds, NIC 1987 for the 50th round, NIC 1998 for the 55th and 61st rounds, and NIC 2004 for the 66th round, as a starting point concordance between26 sectors and NIC-1970, 1987, 1998 and 2004 was done.
Employment has then been computed as follows:
-
Work Participation Rates (WPRs) by the UPSS from the EUS are applied to the corresponding period’s census population6 of Rural Male, Rural Female, Urban Male and Urban Female to find the number of persons employed in the four segments
-
The 26-industry distribution of employment from EUS is applied to the number of persons employed in Step I to obtain Lij for each industry where i=1 for rural and 2 for urban sectors, and j=1 for male and 2 for female employees.
-
Total persons in a year were obtained for each industry as the sum of Lij over gender and sectors, ΣiΣjLij
For extrapolation backward to 1980-81 to 1982-83, the interpolation of the broad industrial classification of the 32nd round (1977-78) and the 38th round (1983-84) is used. So the estimates from the 32nd round are mainly used as control numbers.
b) Measuring composition index
The composition of the labour force is of considerable importance in the context of productivity measurement, and a widely used methodology to capture changes in labour composition is given by Jorgenson, Gollop and Fraumeni (JGF) (1987). In growth accounting methodology, labour input is measured as an index of labour service flows. It accounts for changes in labour composition in terms of labour characteristics such as educational attainment, age or gender and, thus, accounts for heterogeneity of the labour force.
In this method the aggregate labour input Lj of sector ‘j’ is defined as a Törnqvist volume index of persons worked by individual labour types ‘l’ as follows7:
where Δln Li,j indicates the growth of persons employed by labour type ‘l’ for sector ‘j’and weights are given by the period average shares of each type in the value of labour compensation, such that the sum of shares over all labour types is unity. It is assumed that the persons employed are paid their marginal productivities8 and since the study also assumes that marginal revenues are equal to marginal costs, the weighting procedure ensures that inputs that have a higher price also have a larger influence in the input index. Let Lj indicate the total persons employed in sector ‘j’ by all types Lj= Σ Li,j then the change in labour input (LI) can be decomposed as follows:
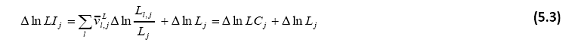 The first term on the right-hand side, i.e., Δln LCj indicates the change in labour composition and the second term indicates the change in total persons employed in sector ‘j’. The index of aggregate labour composition, thus, measures the changes in the sex-age-education-occupation composition of the labour input in the economy. However, the use of this method is data-intensive.
Due to data limitations of the sample size becoming very small as it is tried to estimate persons employed and earnings by industry by all the characteristics9, the present study has computed labour composition using only the education characteristic in the JGF methodology. For the labour composition index, the data required is employment by education by industry and earnings (compensation) for each cell. The labour composition index has been computed using five education categories10, namely, up to primary, primary, middle, secondary & higher secondary, and above higher secondary. There are, thus, five types of persons employed for each of the 26 study industries. It is estimated for the total persons employed in these industries in India for the 38th, 43rd, 50th, 55th, 61st and 66th rounds of the NSSO, with 1983 (38th round) equal to 100 so as to assess the temporal changes in labour skill. Since the series is required from 1980-81, the study has extrapolated it backwards from 1983 and interpolated between the major rounds. The composition index is recomputed with base 1980 as 100.
Therefore, the following steps have been performed:
-
The first step involves computing the proportions of the distribution of persons employed by the five educational groups for all 26 industries for all the major rounds11
-
These proportions are then applied to the number of employed persons in different industries to obtain the distribution of persons by education groups.
-
The earnings data is estimated from the NSSO, which relates mainly to regular and casual persons employed. It may, however, be mentioned that even for these two groups, for a large number of persons employed, wages are either missing or given as zero.
- For earnings of self-employed persons12, two approaches have been adopted. First, a Mincer wage equation has been estimated and the sample selection bias is corrected by using Heckman’s13 two-step procedure. The function has been applied to the earnings of casual and regular employees where the earnings have been regressed on the dummies of age, gender, education, location, marital status, social exclusion and industry. The identification factors used in the first stage are age, gender, marital status and type of household/size of household. The corresponding earnings of the self-employed are obtained as the predicted value with similar traits. The average wages per day are then computed for persons employed in different types of employment, i.e., self-employed, regular and casual combined, whose wages are more than zero.
Second, earnings of the self-employed have also been estimated from the monthly consumption expenditure of these households. In this approach, first the total monthly consumption expenditure is divided by the number of employed persons in the household to get the total monthly consumption expenditure per employed person. Then, the ratio of wage earnings to total monthly consumption expenditure per employed person has been calculated for each industry by UPSS status. Assuming the consumption-earnings ratio to be the same for casual and self-employed persons, the ratio for casual labour is used for self-employed persons and this ratio is multiplied by the total monthly consumption expenditure per self-employed person to get the earnings of self-employed persons. However, if the earnings thus obtained are higher than the earnings obtained from the Mincer equation, then the latter are used. So, the lower of the two earnings- obtained from the Mincer equation or the earnings based on consumption expenditure- is taken to be the earnings of self-employed persons. It is to be noted that the two methods are used because they are based on i) household characteristics and ii) consumption expenditure. By combining the two, the study has moderated any upward bias in the estimation of wages for self-employed.
Once the above steps are taken to find the educational distribution of all employed persons in all the six rounds and their corresponding wages, the labour composition index is computed14.
5.2.2 Trend Growth Rate of Labour Input for 26 Industries of the Indian Economy
In this section, an analysis of the growth of the labour input is presented. The growth in persons employed and the labour composition for the entire period is given in Table 5.1. The growth rate of labour input (Index of persons employed multiplied by the index of labour composition) is summarised in Table 5.2.
Growth of persons employed
The rate of growth of persons employed is very different in different industries, reflecting a structural change during the period. For the full period the trend average growth of persons employed is 1.78 per cent. However, there have been changes in terms of employment growth in the Indian economy. While some sectors grew very fast, others remained stagnant during this period. Agriculture and mining & quarrying, which together employ the largest share of employed persons, has almost zero employment growth in the recent period. Consequently, their share in total employment has reduced from almost two-third to one-half. Among the sub-sectors of manufacturing it is found that very few sectors show rapid trend growth in employment. Construction is one important sector that has consistently experienced rapid employment growth. It has low labour productivity but vast employment potential and can be tapped for employment opportunities. Most sectors have registered a decline in the rate of employment growth in the recent decade15 except for textiles, wood, paper, transport equipment, hotels, construction and education and health.
Growth of Labour Composition Index
The growth in labour composition index is mainly the measurement of change in the educational skills of the employed persons over the period and their rewards for these skills. In India, the share of high-skilled labour (with education above higher secondary) has increased from a mere 2.4 per cent to almost 9 per cent. At the industry level, the growth in labour composition was the fastest in machinery, nec; chemical & products; other services; mining and quarrying; pulp & paper; and rubber & plastic products, but very slow in wood and products of wood; agriculture; basic metals and construction. Thus, the skill composition of each industry has changed differently over the period.
Table 5.1: Trend Growth Rates of Persons Employed by Industry, 1980 to 2008 and
Growth Rate of Labour Composition Index by Industry, 1980 to 2008 |
(% per annum) |
Industry No. |
Industry Description |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
Persons Employed by Industry |
Agriculture Labour
Composition Index |
1 |
Agriculture |
1.17 |
-0.01 |
0.88 |
0.19 |
0.48 |
0.26 |
2 |
Mining& Quarrying |
1.77 |
0.86 |
1.54 |
0.61 |
2.68 |
1.13 |
3 |
Food products, Beverages & Tobacco |
2.75 |
-0.55 |
1.92 |
0.77 |
0.92 |
0.81 |
4 |
Textiles, Leather & Footwear |
-0.73 |
4.7 |
0.64 |
0.88 |
0.85 |
0.87 |
5 |
Wood & products |
0.34 |
1.56 |
0.65 |
-0.08 |
0.9 |
0.17 |
6 |
Pulp, Paper, Paper products, Printing& Publishing |
2.9 |
4.32 |
3.25 |
0.92 |
1.46 |
1.05 |
7 |
Coke, Refined Petroleum & Nuclear fuel |
8.21 |
-8.28 |
4.07 |
0.37 |
2.19 |
0.83 |
8 |
Chemicals & Chemical products |
3.5 |
-0.07 |
2.6 |
1.13 |
1.47 |
1.22 |
9 |
Rubber and Plastic products |
8.07 |
-2.98 |
5.3 |
1.49 |
-0.33 |
1.04 |
10 |
Other Non-Metallic Mineral Products |
1.41 |
3.18 |
1.86 |
1.16 |
0 |
0.87 |
11 |
Basic Metals & Fabricated Metal products |
2.65 |
1.76 |
2.43 |
0.35 |
0.56 |
0.4 |
12 |
Machinery, nec. |
6.11 |
-0.36 |
4.49 |
2.36 |
0.61 |
1.92 |
13 |
Electrical & Optical equipment |
5.13 |
0.81 |
4.04 |
0.31 |
1.35 |
0.57 |
14 |
Transport equipment |
0.65 |
9.65 |
2.91 |
0.79 |
0.88 |
0.81 |
15 |
Manufacturing, nec. |
3 |
3.45 |
3.12 |
0.86 |
0.61 |
0.8 |
16 |
Electricity, Gas & Water Supply |
2.06 |
-0.57 |
1.4 |
0.8 |
1.19 |
0.9 |
17 |
Construction |
5.13 |
8.44 |
5.96 |
0.42 |
0.44 |
0.42 |
18 |
Trade |
4.06 |
2.81 |
3.75 |
0.79 |
0.73 |
0.77 |
19 |
Hotels &Restaurants |
3.4 |
4.88 |
3.77 |
0.37 |
0.96 |
0.52 |
20 |
Transport & Storage |
4.18 |
4.12 |
4.17 |
0.75 |
0.65 |
0.73 |
21 |
Post & Telecommunications |
6.08 |
5.26 |
5.87 |
0.59 |
0.51 |
0.57 |
22 |
Financial services |
4.81 |
4.17 |
4.65 |
0.52 |
0.26 |
0.46 |
23 |
Public administration and Defence |
1.39 |
-1.79 |
0.59 |
0.65 |
0.53 |
0.62 |
24 |
Education |
3.67 |
5.15 |
4.04 |
0.65 |
0.56 |
0.62 |
25 |
Health & Social work |
2.99 |
5.17 |
3.54 |
0.94 |
0.62 |
0.86 |
26 |
Other Services |
4.16 |
3.51 |
4.00 |
0.68 |
2.56 |
1.15 |
Source: Authors’ calculations |
The growth rate of labour input (index of persons employed multiplied by the index of labour composition) across industries is shown in Table 5.2. It reveals that labour input grew the fastest in post & telecommunications; machinery nec; construction; rubber & plastic products; other services and financial services.
It is observed that the growth rates of labour input were higher than those of persons employed because of the contribution of labour composition.
Table 5.2: Growth Rate of Labour Input by Industry, 1980 to 2008 |
(% per annum) |
Industry No. |
Industry Description |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
1.36 |
0.48 |
1.14 |
2 |
Mining &Quarrying |
2.37 |
3.54 |
2.67 |
3 |
Food products, Beverages & Tobacco |
3.51 |
0.36 |
2.72 |
4 |
Textiles & Leather products |
0.15 |
5.55 |
1.51 |
5 |
Wood & Products |
0.27 |
2.46 |
0.82 |
6 |
Pulp, Paper, paper products, printing and publishing |
3.81 |
5.78 |
4.31 |
7 |
Coke, Refined petroleum, Nuclear fuel |
8.58 |
-6.09 |
4.90 |
8 |
Chemicals &products |
4.62 |
1.40 |
3.81 |
9 |
Rubber & Plastic products |
9.57 |
-3.30 |
6.33 |
10 |
Other Non-Metallic mineral products |
2.57 |
3.18 |
2.72 |
11 |
Basic metals & Fabricated metal products |
3.00 |
2.32 |
2.83 |
12 |
Machinery, nec. |
8.48 |
0.24 |
6.41 |
13 |
Electrical &Optical equipment |
5.44 |
2.16 |
4.62 |
14 |
Transport equipment |
1.44 |
10.52 |
3.72 |
15 |
Manufacturing, nec. |
3.87 |
4.06 |
3.91 |
16 |
Electricity, Gas & Water Supply |
2.86 |
0.62 |
2.30 |
17 |
Construction |
5.54 |
8.88 |
6.38 |
18 |
Trade |
4.85 |
3.54 |
4.52 |
19 |
Hotels & Restaurants |
3.78 |
5.84 |
4.29 |
20 |
Transport & Storage |
4.93 |
4.77 |
4.89 |
21 |
Post &Telecommunications |
6.66 |
5.76 |
6.44 |
22 |
Financial services |
5.33 |
4.43 |
5.11 |
23 |
Public administration and Defence |
2.05 |
-1.26 |
1.22 |
24 |
Education |
4.32 |
5.71 |
4.67 |
25 |
Health & Social work |
3.93 |
5.78 |
4.40 |
26 |
Other services |
4.84 |
6.07 |
5.15 |
Source: Authors’ calculations. |
5.3 Capital Input-Data source, Methodology and Estimat
5.3.1 Data Sources and Methodology
As in the case of labour input where workers differ in terms of skill and experience, capital also consists of different vintages and asset types and these assets are not directly used in the production process; rather, the service delivered by these assets are the inputs to production. However, the empirical measurement of capital services is complicated due to the difficulty in quantifying the flow of capital services delivered by a unit of capital. Therefore, the usual practice is to assume proportionality between capital services and capital stock at the individual asset level (Hulten, 1986; Jorgenson, 1963; Jorgenson and Griliches, 1967). However, one should take account of the differences in the services delivered by different asset types, as each asset type differs in terms of its efficiency level. This would mean that even though one would assume proportionality between capital stock and capital service at the individual asset level, the weights differ across asset types and over time depending on the marginal productivity of each asset type16. Since marginal productivities are unobservable, one could, under neoclassical assumptions, approximate them by the prices of capital services delivered by each type of asset. Using this line of reasoning, Jorgenson (1963) and Jorgenson and Griliches (1967) have developed aggregate capital service measures that take into account the heterogeneity of assets. Using the Tornqvist approximation to the continuous Divisia index under the assumption of instantaneous adjustability of capital, capital services growth rate for asset type k is derived as a weighted growth rate of individual capital assets, the weights being the compensation shares of each asset, i.e.,
 The rental price of capital Pk,tK reflects the price at which the investor is indifferent between buying and renting the capital good for a one-year lease in the rental market17. of taxation the rental price equation can be derived as under (see Christensen and Jorgenson, 1969; Jorgenson and Griliches, 1967):
 with it representing the nominal rate of return, δk the depreciation rate of asset type k, and Plk,t the investment price of asset type k. This formula shows that the rental fee is determined by the nominal rate of return, the rate of economic depreciation and the asset specific capital gains18. Ideally taxes should be included to account for differences in tax treatment of the different asset types and different legal forms (household, corporate and non-corporate). The capital service price formulas above should then be adjusted to take these tax rates into account. However, this refinement would require data on capital tax allowances and rates by industry and year, which is beyond the scope of this database. Available evidence for major European countries shows that the inclusion of tax rates has only a very minor effect on growth rates of capital services and TFPG (Erumban, 2008a).
Since our measure of capital input takes account of asset heterogeneity, it was essential to obtain investment data by asset type. The study distinguishes between 4 different asset types -construction, transport equipment, non-ICT machinery and ICT equipment (hardware, software and communication equipment)19. Though India is a leading ICT software-producing country, there is little information about the use of ICT as an input in the production process across different industries. Therefore, multiple sources of information have been used for the construction of our database on capital services. This includes NAS, which provides information on broad sectors of the economy, the ASI covering the formal manufacturing sector, the NSSO rounds for unorganised manufacturing, Input-Output tables and CMIE’s Prowess firm-level database. Despite this, the final estimates are fully consistent with the aggregate data obtained from NAS. Despite these attempts, industry-level estimates of ICT investment are not satisfactory and are not used in the present version of capital input series. The various sources of data and the construction of the relevant variables are discussed in detail below.
(a) Investment in non ICT Capital Assets
Industry-level estimates of capital input require detailed asset-by-industry investment matrices. The basic data source for the non-ICT assets comprising construction, transport equipment and non-ICT machinery is the NAS20. However, in the public domain NAS provides only information on aggregate capital formation by industry of use for 9 broad sectors. The CSO has provided detailed asset-wise data underlying the published aggregate gross fixed capital formation by these broad industry groups, separately for public and private sectors. The public sector units were aggregated from administrative, departmental and non-departmental enterprises. Table 5.3 provides an overview of asset types available in NAS and their corresponding KLEMS categories.
Table 5.3: Capital Asset Types in National Accounts Statistics
vis-à-vis those in India KLEMS |
NAS Asset Types |
Our Study Asset Types |
Public Sector |
Buildings |
Construction |
Other construction |
Construction |
Transport equipment21 |
Transport equipment |
Machinery & Equipment |
Machinery & Equipment(ICT is excluded) |
Software (1999-2000 onwards) |
ICT |
Private Sector |
Residential buildings |
Construction |
Non-residential buildings |
Construction |
Other construction |
Construction |
Machinery & Equipment (incl. transport equipment) |
Machinery & Equipment (transport equipment and ICT are excluded) |
Software (1999-2000 onwards) |
ICT |
| Source: CSO and NAS, various issues. |
Total investment in each asset category is calculated as the sum of private and public sector investment in each asset. Investment in transport equipment is not available separately for the private sector. Therefore, it has been derived using the ratio of transport equipment to total machinery (including transport equipment) in the public sector22. Then the sum of transport equipment in the public sector and the derived investment in the private sector is considered as the total investment in transport equipment. Investment in machinery & equipment, which is defined as the sum of machinery & equipment in the public sector and total machinery & equipment excluding derived transport equipment in the private sector, is inclusive of ICT as it was not separately available. For the aggregate economy, ICT investment has been subtracted from machinery after constructing the ICT investment series independently, which will be discussed subsequently.
NAS provides data for only 9 broad sectors, while the study has 26 study sectors, which necessitated further splitting of some NAS sectors. The manufacturing sector investment data was disaggregated into 13 sub-sectors at the 2-digit level of NIC 1998 using ASI and NSSO data, which will be discussed in detail subsequently. Investment series in the service sector has been split into sub-sectors using two alternative approaches—value added shares and capital/labour ratio in the aggregate industry. However, the final data used are based on value added shares, as a sensitivity analysis did not show a significant difference between the two.
In order to split the aggregate capital formation in the organised manufacturing sector into 13 study sectors, ASI data has been used. However, the published data does not provide any asset- wise investment information; it consists of only the aggregate capital formation or the book value of fixed capital. Most studies in the past have measured gross investment as the difference between the book value of the asset in period t and in period t-1 and added depreciation in period t to that. This approach has the deficiency of comparing two different samples reported in two different years, where the number of firms/factories might be different. In particular, while using this approach at the industry level, for detailed asset categories it might generate massive negative investment. An alternative approach has been followed, using the ASI’s definition of gross fixed capital formation (GFCF). The ASI defines GFCF as actual additions (newly purchased, second-hand and own construction) minus deductions plus depreciation adjustment for discarded assets during the year. This approach is based on a single year’s sample and helps to avoid potential huge negative investment series, and is also consistent with the published ASI GFCF series. The yearly detailed volumes for the years 1964-65 were used to derive the GFC by asset type directly23. For the period 1983-84 to 2004-05 the ASI provides data on fixed assets. Data for missing years are interpolated using the changes in investment using the book value method. Table 5.4 provides an overview of the asset categories available in ASI and the relevant asset categories in our study to which they are attributed. Though ASI provides investment in land, for reasons of NAS consistency the study excludes it from the KLEMS database. Once investment in each of these assets and industries are generated using ASI data, we apply this industry-asset distribution to the published aggregate NAS GFCF series for the organised manufacturing sector. It may also be noted that from 1960-61 to 1971-72, ASI data are for the census sector and from 1973-74 onwards they are for the factory sector. In order to make these two series comparable over years, the data prior to 1972 has been converted to the factory sector using the factory/census ratio in 1973. Thus, after these adjustments, investment data for 13 manufacturing sectors is obtained, by asset type, consistent with the NAS aggregates.
Table 5.4: Asset Types in ASI and India KLEMS |
ASI Asset Types |
Our study Asset Types |
Land |
Excluded |
Buildings |
Buildings & Construction |
Plants & Machinery |
Machinery &Equipment (ICT is excluded) |
Transport equipment |
Transport equipment |
Computer equipment including Software (from 1998) |
ICT equipment |
Pollution control equipment (from 2000) |
Machinery & Equipment |
| Source: CSO, NAS Various Issues. |
The data required to create the gross investment series for the 13 sectors of the unorganised manufacturing sector are obtained from various rounds of NSSO surveys on unorganised manufacturing. Four rounds of NSSO surveys are used that cover the period 1989-2006. These are the 45th round (1989-90), 51st round (1994-95), 56th round (1994-95) and 62nd-round (2005-06). Unit-level data has been aggregated to 13 study sectors using the appropriate concordance tables. The NSSO provides net addition to owned assets during the reference year within the block of fixed assets, and this is used as a measure of investment. Asset classification in the NSSO has changed over various rounds and, therefore, it has been ensured that these match the study classification as shown in Table 5.5.
The investment series arrived at for four rounds are interpolated to obtain the annual time series of unorganised GFCF by asset type. As in the case of the registered sector, once the investment by asset type across industries is constructed, the asset-industry distribution is applied to the published NAS aggregate GFCF in unregistered manufacturing to obtain NAS-consistent GFCF by asset type and industry.
Table 5.5: Asset Categories in NSSO Rounds |
NSSO
Asset Types |
45th Round
(1989-90) |
51st Round
(1994-95) |
56thRound
(2000-01) |
62ndRound
(2005-06) |
Our
Study
Asset |
1 |
Land |
Land &
Building |
Land & Buildings |
Land & Buildings |
Construction
(land is excluded) |
2 |
Building & other construction
Plant & Machinery |
Other construction
Plant & Machinery |
Plant & Machinery |
Plant & Machinery |
Machinery & Equipment |
3 |
Transport equipment |
Transport equipment |
Transport equipment |
Transport equipment |
Transport equipment |
4 |
Tools & other fixed assets |
Tools & Other fixed assets |
Tools & other fixed assets |
Tools & other fixed assets
Software & hardware |
ICT equipment |
Note: in all the cases, if ICT assets are not separately provided, they are excluded from machinery equipment, after estimating ICT investment independently (see section on ICT investment). For the 56th and 62nd rounds, land is separated from land & buildings using land/land & building ratio from the 51st round.
Source: NSSO Rounds. |
(b) Investment in ICT Assets
Since official statistics on ICT investment is still not comprehensive in India, the study relies on alternative sources to impute ICT investment. However, whenever the information is available from official sources, we exploit such information and ensure consistency with official statistics. Total economy ICT investment (for hardware and communication equipment) series is arrived at using the commodity flow approach24. In this approach, investment in hardware and communication equipment can be estimated using information on the total domestic availability of these goods and its investment component. This requires the use of input-output tables, in combination with NAS and trade statistics. The study defines the investment in ICT asset i as:
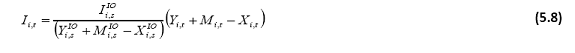 where Ii,t is the current investment, Y is gross domestic output, M is imports and X is exports. Superscript IO refers to input-output tables, i.e., for instance,  indicates investment in asset type i (since the study considers computer hardware and communication equipment, i=1,2, i.e., hardware and communication equipment) in year s (where s is the benchmark year for IO table) obtained from the input-output table. All other variables without the superscript IO are time-series data obtained from NAS. Following previous studies, the study defines industry 30 according to International Standard Industrial Classification (ISIC) 3.1 (office equipment and machinery) as computer hardware and industry 32 (radio, TV and communication equipment) as communication equipment. The study obtains investment in hardware and communication equipment, along with total domestic output, imports and exports for 6 benchmark years, 1983-84, 1989-90, 1993-94, 1998-99, 2003-04, 2006-07, from input-output tables published by the CSO. There is no strict concordance between ISIC 3.1 and India’s input-output table classification and, therefore, the study considers the Indian IO sector ‘office computing and accounting machinery’ as hardware and ‘communication equipment and electronic equipment including TV’ as communication equipment. This information is used to compute the first part of equation (5.8). Then, using time-series data on gross output obtained from the India KLEMS25 output database, and exports and imports obtained from UN-Comtrade statistics, the study constructs a series of ICT investment using equation (5.8). indicates investment in asset type i (since the study considers computer hardware and communication equipment, i=1,2, i.e., hardware and communication equipment) in year s (where s is the benchmark year for IO table) obtained from the input-output table. All other variables without the superscript IO are time-series data obtained from NAS. Following previous studies, the study defines industry 30 according to International Standard Industrial Classification (ISIC) 3.1 (office equipment and machinery) as computer hardware and industry 32 (radio, TV and communication equipment) as communication equipment. The study obtains investment in hardware and communication equipment, along with total domestic output, imports and exports for 6 benchmark years, 1983-84, 1989-90, 1993-94, 1998-99, 2003-04, 2006-07, from input-output tables published by the CSO. There is no strict concordance between ISIC 3.1 and India’s input-output table classification and, therefore, the study considers the Indian IO sector ‘office computing and accounting machinery’ as hardware and ‘communication equipment and electronic equipment including TV’ as communication equipment. This information is used to compute the first part of equation (5.8). Then, using time-series data on gross output obtained from the India KLEMS25 output database, and exports and imports obtained from UN-Comtrade statistics, the study constructs a series of ICT investment using equation (5.8).
This approach allows us to generate investment series only for the total economy, as an industry breakdown is not possible with input-output tables. Moreover, this method cannot be used to infer any information on software investment, as the main source of data for this approach, i.e., input-output tables, contains no information on software. De Vries et al. (2007) suggest using the elasticities of hardware to software investment, estimated using a fixed effect panel regression of software on hardware and a set of control variables. In order to arrive at software investment series, the study first computes software-to-hardware ratio for the years after 2000. The study uses the information on software series from NAS and the hardware data obtained using the commodity flow approach. This ratio has been extrapolated linearly backwards until 1970 to generate the software series for previous years. This provides us with a complete series of ICT investment, hardware, software and communication for the total economy for the period 1970-2004. The present version of the database does not provide ICT estimates for 26 KLEMS sectors. Since the aggregate estimates are based on official information from input-output tables, the study considers them reliable. However, such information is hardly available at the sectoral level. Though the study made an attempt to impute ICT investment series at the sectoral level, exploiting several data sources that provide some information on ICT investment in Indian industries, the estimates are less satisfactory and require further improvement.
(b) Investment Prices by Asset Types
In order to compute asset-wise capital stock using PIM (equation 5.6) and rental price (equation 5.7), the study requires asset-wise investment price deflators. The CSO has provided asset-wise deflators for all three asset types with base 1999-2000. These deflators are directly used for all the non-ICT assets. Price measurement for ICT assets has been an important research topic in recent years. Until recently, large differences existed in the methodology to obtain deflators for ICT equipment between countries, and the use of a single harmonised deflator across countries was widely advocated and used (Colecchia and Schreyer, 2001; Schreyer 2002; Timmer and van Ark, 2005). This deflator was based on the US deflators for computer hardware, which were commonly seen as the most advanced in terms of accounting for quality changes using hedonic pricing techniques (Triplett, 2006). For India, we use the harmonisation procedure suggested by Schreyer (2002), where the US hedonic deflators are adjusted for India’s domestic inflation rates.
(c) Initial Stock, Depreciation Rates and Rate of Return
As is evident from equations 5.4 to 5.7, estimate of capital input requires time-series data on asset-wise capital stock. Capital stock has been constructed using PIM, where the capital stock (S) is defined as a weighted sum of past investments with weights given by the relative efficiencies of capital goods at different ages, which requires data on current investment by asset type, investment prices by asset type and depreciation rate. Also, for the practical implementation of PIM to estimate asset-wise capital stock, an estimate of initial benchmark stock is required (see Erumban, 2008b for an in-depth discussion on this issue). NAS provides estimates of net capital stock since 1950 for all the broad sectors. The NAS estimate of real net capital stock in 1950 (in 1999-2000 prices) is taken as the benchmark stock for all non-manufacturing sectors, and for manufacturing sectors the same is taken for the year 196426. However, since the NAS estimate is available only for broad sectors and for aggregate capital, the study uses our industry-asset distribution of GFCF in order to create net fixed capital stock estimates by asset type for all 26 sectors. NAS also provides detailed tables on the assumed life of assets used for computing capital stock, for private units, administrative units as well as departmental and non-departmental units by asset type27. The study uses these estimates of lifetime to derive appropriate depreciation rates for non-ICT assets, using a double declining balance rate. The study assumes 80 years of lifetime for buildings, 20 years for transport equipment, and 25 years for machinery and equipment. The depreciation rates for ICT assets, viz., hardware and software and communication equipment, are taken from the EU KLEMS. The final depreciation rates used in the study are given in Table 5.6 by asset type. Subsequently, the capital stock series is built by asset types for all the 26 industries using our GFCF series from 1950 (1964) onwards for the non-manufacturing (manufacturing) sectors.
Table 5.6: Depreciation Rate by Asset Type used in
Computation of Capital Input |
Asset Type |
Depreciation Rate (%) |
Building & Construction |
2.5 |
Transport equipment |
10.0 |
Non-ICT machinery |
8.0 |
Hardware & Software |
31.5 |
Communication equipment |
11.5 |
Source: NAS and EU KLEMS. |
Our measure of capital input is arrived at by using equation(5.4), for which estimates of rental prices (see equation 5.7) is also required. Assuming that the flow of capital services is proportional to the capital stock at the individual asset level, aggregate capital flows can be obtained using a translog quantity index by weighting growth in the stock of each asset by the average share of each asset in the value of capital compensation, as in (5.4). The rate of return (i) in equation (5.7) represents the opportunity cost of capital, and can be measured either as an internal (or ex post) rate of return, or as an external (ex ante) rate of return28. The present version of the database uses an external rate of return, proxied by average of return on government securities and prime lending rate obtained from the Reserve Bank of India29. The capital gain component in equation (5.7) is excluded while estimating rental price using external rate of return, obtaining 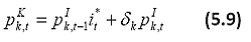
Where i* is the real rate of return, i.e., nominal interest rate adjusted for CPI inflation rate
5.3.2 Trend Growth Rate of Capital Input for 26 Industries of the Indian Economy
Capital service growth rates for each of the 26 study industries, calculated using asset-wise investment series at the disaggregated industry level by employing equation (5.4), are presented in Table 5.7. The table also lists the capital stock growth rates for the same set of Industries.
Table 5.7: Trend Growth of Capital Stock and Capital Services-26 Sectors |
(% per annum) |
Industry No. |
Industry Description |
Capital Stock |
Capital Service |
1980
to
1999 |
2000
to
2008 |
1980
to
2008 |
1980
to
1999 |
2000
to
2008 |
1980
to
2008 |
1 |
Agriculture, Forestry &Fishing |
2.09 |
5.23 |
2.88 |
2.53 |
6.45 |
3.51 |
2 |
Mining & Quarrying |
6.94 |
3.71 |
6.13 |
7.25 |
3.22 |
6.24 |
3 |
Food Products, Beverages & Tobacco |
6.53 |
4.19 |
5.94 |
7.34 |
4.72 |
6.69 |
4 |
Textiles & Leather products |
9.26 |
9.59 |
9.34 |
10.17 |
8.97 |
9.87 |
5 |
Wood & products of wood |
10.21 |
12.22 |
10.72 |
10.70 |
11.71 |
10.95 |
6 |
Pulp, Paper, Paper products, Printing & Publishing |
4.94 |
6.47 |
5.33 |
5.83 |
8.28 |
6.44 |
7 |
Coke, Refined petroleum products & Nuclear fuel |
10.22 |
12.18 |
10.71 |
11.56 |
11.79 |
11.62 |
8 |
Chemicals & Chemical products |
10.04 |
7.77 |
9.47 |
11.15 |
7.02 |
10.11 |
9 |
Rubber & Plastic products |
13.01 |
6.00 |
11.25 |
13.99 |
5.70 |
11.91 |
10 |
Other Non-Metallic Mineral products |
6.48 |
8.22 |
6.91 |
8.59 |
8.55 |
8.58 |
11 |
Basic Metals & Fabricated Metal products |
9.33 |
8.18 |
9.04 |
10.59 |
7.68 |
9.86 |
12 |
Machinery, nec. |
2.86 |
8.95 |
4.39 |
3.56 |
9.64 |
5.09 |
13 |
Electrical & Optical equipment |
7.11 |
7.39 |
7.18 |
8.60 |
8.25 |
8.51 |
14 |
Transport equipment |
10.61 |
12.87 |
11.18 |
11.90 |
12.55 |
12.06 |
15 |
Manufacturing, nec |
9.30 |
13.14 |
10.27 |
9.22 |
12.09 |
9.94 |
16 |
Electricity, Gas & Water Supply |
6.89 |
4.33 |
6.25 |
7.05 |
4.11 |
6.31 |
17 |
Construction |
6.38 |
15.45 |
8.66 |
6.42 |
15.41 |
8.68 |
18 |
Trade |
3.51 |
8.94 |
4.87 |
3.78 |
9.81 |
5.30 |
19 |
Hotels & Restaurants |
5.92 |
7.30 |
6.27 |
6.44 |
7.46 |
6.70 |
20 |
Transport & Storage |
5.18 |
9.62 |
6.29 |
5.48 |
9.68 |
6.54 |
21 |
Post & Telecommunications |
10.52 |
6.66 |
9.55 |
11.28 |
6.90 |
10.18 |
22 |
Financial services |
14.22 |
0.93 |
10.88 |
15.06 |
0.98 |
11.52 |
23 |
Public administration & Defence |
4.03 |
5.79 |
4.47 |
4.19 |
5.81 |
4.59 |
24 |
Education |
8.35 |
15.67 |
10.19 |
8.52 |
15.60 |
10.30 |
25 |
Health & Social work |
9.18 |
16.85 |
11.10 |
9.30 |
16.8 |
11.19 |
26 |
Other services |
3.06 |
9.77 |
4.75 |
3.19 |
10.55 |
5.04 |
Source: Authors’ calculations. |
5.4 Intermediate inputs: Data Source, Methodology and Estimates
5.4.1 Data Sources and Methodology
An important advantage of the gross output production function is that it recognises the explicit role of intermediate inputs. This is critical because intermediate inputs may be an important component of some industries’ output.
Only by accurately accounting for intermediate inputs, through the use of inter-industry transaction tables and the gross output concept, Indian economic growth can be allocated to its sources in individual industries. Failure to quantify intermediate inputs may lead us to miss both the role of key industries that produce intermediate inputs and the importance of intermediate industries that use them. This section discusses the sources of data and methods for construction of intermediate inputs for 26 industries and broad sectors from 1980-2008. The study discusses both the raw data sources and the adjustments that have been made to generate the comprehensive time series of Intermediate inputs consistent with the official National Accounts. The methodology for measuring industry output, intermediate inputs and value added was developed by Jorgenson, Gallop and Fraumeni (1987) and extended by Jorgenson (1990a). The cornerstone of this approach is a time series of input-output (IO) tables that give the flows of all commodities in the economy, as well as payments to primary factors. Every commodity is accounted for, whether produced by a domestic source or imported, and every use is noted, whether purchased by an industry or by a final demand element. All payments to factors of production, i.e., labour and capital, are accounted for so that all income elements of GDP are included. The methodology of constructing time series on energy, material and services input for the European economy has been elucidated in Timmer et al. (2010, Chapter 3). Following a similar approach as explained in Jorgenson et al. (2005, Chapter 4) and Timmer et al. (2010, Chapter 3), the time series on intermediate inputs for the Indian economy has been constructed.
The study identifies three main categories of Intermediate inputs: Energy input, Service input and Material input.
Intermediate Inputs are broken down into energy, material and services, based on input- output transaction tables using a standard NIC product classification. The following five energy types (and products) have been classified as the Energy input: Coal & Lignite, Petroleum products, Natural gas, Gas (LPG) and Electricity. For electricity used in the electricity sector, since there is a good amount of inter-firm sale and purchase of electricity, it has been treated as material rather than as energy.
The following 14input items have been classified as the Service input: Water supply, Railway transport services, other transport services, Storage & warehousing, Communication, Trade, Hotels & restaurants, Banking, Insurance, Ownership of dwellings, Education & research, Medical &health, other services and public administration.
All other intermediate inputs barring the above-mentioned 19 inputs are classified as material input.
a) Data Sources for Intermediate Inputs
This project uses multiple data sources to construct time series on intermediate inputs for 26 industries at current and constant prices. The details of the data sources are as follows:
- National Accounts Statistics 2011, 2009, 2007 and back series
- WPI, Office of the Economic Adviser, Ministry of Commerce and Industry
- Supply and Use Tables (known as the Input-Output Transaction Tables) for Benchmark Years: 1978, 1983, 1989, 1993, 1998 and 2003
The key building block for constructing time series on Intermediate Inputs at current prices, as explained in Jorgenson et al. (2005, Chapter 4), is the input-output transaction tables (IOTT), that is, the inter-industry transaction tables that provide a description of industries producing each product and the industries using them. The input-output table gives the inter-industry transactions in value terms at factor cost presented in the form of a commodity x industry matrix where the columns represent the industries and the rows show groups of commodities that are the principal products of the corresponding industries. Each row of the matrix shows in the relevant columns the deliveries of the total output of the commodities to the different industries for intermediate consumption and final use. The entries read down industry columns give the commodity inputs of raw materials and services, which are used to produce outputs of particular industries. The column entries at the bottom of the table give net indirect taxes (NIT) (indirect taxes – subsidies) on the inputs and the primary inputs (income from use of labour and capital), i.e., Gross Value Added (GVA). As the IOTT is in the form of a commodity x industry matrix, the row totals do not tally with the column totals. The difference between each column total and the corresponding row total is due to the inclusion of secondary products, which appear particularly in the case of manufacturing industries. This is so because by-products are also manufactured by industries in addition to their main products. Thus, while determining the entries in the rows, a by-product of an industry is transferred to the sector (commodity row), whose principal product is the same as the by-product under reference. The columns, however, show the total of principal products and by-products of each industry. All the entries in the IOTT are at factor cost, i.e., excluding trade and transport charges and NIT.
The Input Flow Matrix at factor cost, published by the CSO, for 1978 is a 60 x 60 matrix. The absorption matrices for 1983, 1989, 1993 and 1998 have 115 sectors. However, a detailed 130-sector absorption (commodity x industry) matrix for the Indian economy has been published from 2003-04 onwards. The scheme of sectoral classification adopted in IOTT 2003 has undergone significant changes with the disaggregation of some of the sectors that have become significant since the early 2000s.
b) Methodology for the Construction of Intermediate Input Series
I. Current Price Series
The fundamental concept of deriving the time series of energy, material and services at current prices is to compute their shares in intermediate inputs from the IOTT and then apply them to the series of intermediate inputs from the National Accounts. Therefore, as the starting point, a concordance table between the industrial classifications used in our study and the IOTT has been prepared. The 60/115/130 IOTT sectors are aggregated to form 26 Industries.
The 60/115/130 sector commodity inputs going into the production process of output for 26 study industries are aggregated into:
- Value of Energy inputs used
- Value of Material inputs used
- Value of Service inputs used
- Value of Total Intermediate inputs (summation of the above three)
Effectively, the absorption matrix for each of the benchmark years comprising 115 x 115 or 130 x130 sectors have been collapsed into a matrix of dimension 3x26 (three rows and 26 columns):
- By summing the inputs row-wise into EMS inputs and
- By summing sectors column-wise into our industries
Thus, for each benchmark year, estimates are obtained for material, energy and service inputs used to produce gross output in the 26 different Industries. The next step involves projecting a time series of input proportions for 26 Industries over the period 1980 to 2008. For the Benchmark IOTT years, i.e., 1978, 1983, 1989, 1993, 1998 and 2003, proportions of Material inputs, Energy inputs, and Service inputs in total intermediate inputs are calculated. Proportions for intervening years are obtained by linear interpolation of the benchmark proportions. Thus, the intermediate input vector has been projected for 26 Industries from 1980 to 2008.
Here, it is to be noted that intermediate inputs for the industry ‘Public administration & Defence’ is not available in the IOTT. Thus, the estimation of inputs for this industry is obtained using information from the NAS and SNA tables. For years prior to 1999, inputs have been obtained using tables on ‘Final consumption expenditure of Govt. administrative departments’ published by NAS that provide figures on net purchase of commodities by administrative department. This figure is taken for benchmark IOTT years 1978, 1983, 1989, 1993 and 1998.For years after 1999, the SNA tables relating to cross-classification of output/value added by type of economic activity have been used that provide figures on intermediate consumption in ‘Public administration & defence’. This figure is taken for the IOTT benchmark year 2003. Next, for each benchmark year intermediate consumption has been distributed across all IO sectors, using the GFCE proportion to get material, energy and service inputs.
As discussed in Timmer et al.(2010, Chapter 3), to ensure consistency with NAS, proportions of energy, materials and services inputs are applied to the total intermediate input series from National Accounts. The difference between GVO and GVA constructed from official National Accounts provides us with the gap between gross output and value added, which effectively reflects the total intermediate inputs that go into the production process. This gap does not exactly tally with the intermediate inputs estimated from IOTT30. Hence the gap between output and value added of NAS needs to be distributed between material, energy and services. For this purpose, the projected input vector in previous steps has been proportionately adjusted to match this gap between value added and gross output such that when all the inputs at current prices is aggregated, it should exactly match the gap between output and value added.
The following equation must hold true, at current price:
‘E + M + S = Total Intermediate Input consistent with NAS = GVO – GVA’
The study identifies six broad sectors of the total economy. The intermediate input series for three of the six broad sectors, i.e., Manufacturing, Services and total economy, have been aggregated from the disaggregated level using the Tornqvist method of aggregation.
II. Constant Price Series
The approach followed here is to first form the aggregates of materials, energy and services at current prices for each industry from the benchmark Input-Output tables and then develop weighted deflators of materials, energy and service inputs for each of the 26 Industries separately. To construct weighted deflators of materials, energy and service inputs for 26 industries, the WPI from the Office of the Economic Advisor is combined with weights from the IO transaction tables.
Deflators are obtained for each of the 115 sectors (i.e., given in each row of the IO Matrix). Deflators obtained for different input-output sectors have been combined using weights. The weights are based on the column of the relevant industry in the Input-Output table. Different weights have been used for different time periods. Two IOTTs have been used for this purpose—1989 and 1998. The price series based on the 1989 table has been used from 1980 to 1993 and the 1998 table has been used for the price series from 1993 to 2008. Once the two series have been formed, they are spliced. The deflators for material, energy and service inputs for each sector have been used to deflate the current price Intermediate input series to constant price. The time series on intermediate inputs at constant prices of 26 sectors have been aggregated to form higher-level estimates for the broad sectors using the Tornqvist method of aggregation.
5.4.2 Trend Growth Rate of Intermediate Inputs for 26 sectors of the Indian Economy
The trend growth rates of intermediate inputs show considerable variation across industries (Tables 5.8 and 5.9). For the full period 1980-2008, the trend growth rate of real material input for the total economy stands at 6.96 per cent and those of energy and service inputs stand at 7.17 per cent and 6.98 per cent, respectively, indicating that at the economy level, energy input grew the fastest compared with material and services during the period 1980-2008.
The construction sector witnessed the highest tend growth rate in Intermediate Inputs. Material input in Electricity, gas &water supply grew rather slow relative to Energy and Service input for the whole period. The growth rates of Intermediate inputs have been stagnant in the agriculture sector relative to all other broad sectors and the total economy in the period 1980-2008.
Table 5.8: Trend Growth Rate of Real Material Input by Industry, 1980-2008 |
(% per annum) |
Industry No. |
Industry Description |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
1.78 |
2.68 |
2.01 |
2 |
Mining & Quarrying |
7.48 |
10.28 |
8.18 |
3 |
Food products, Beverages & Tobacco |
5.26 |
9.46 |
6.31 |
4 |
Textiles & Leather products |
6.53 |
6.88 |
6.62 |
5 |
Wood and products of wood |
3.51 |
-2.50 |
2.00 |
6 |
Pulp, Paper, Paper products, Printing & Publishing |
6.04 |
6.73 |
6.21 |
7 |
Coke, Refined Petroleum& Nuclear fuel |
4.71 |
10.29 |
6.11 |
8 |
Chemicals & products |
8.87 |
8.26 |
8.72 |
9 |
Rubber & Plastic products |
11.34 |
9.47 |
10.87 |
10 |
Other Non-Metallic Mineral products |
10.12 |
8.91 |
9.82 |
11 |
Basic Metals& Fabricated Metal products |
6.45 |
4.65 |
6.00 |
12 |
Machinery, nec. |
5.61 |
2.04 |
4.71 |
13 |
Electrical & Optical equipment |
11.61 |
15.06 |
12.48 |
14 |
Transport Equipment |
8.37 |
2.82 |
6.98 |
15 |
Manufacturing, nec |
9.91 |
12.08 |
10.46 |
16 |
Electricity, Gas & Water Supply |
6.84 |
2.31 |
5.70 |
17 |
Construction |
6.70 |
13.81 |
8.49 |
18 |
Trade |
3.86 |
6.74 |
4.59 |
19 |
Hotels & Restaurants |
6.28 |
11.16 |
7.51 |
20 |
Transport & Storage |
7.62 |
11.43 |
8.57 |
21 |
Post & Telecommunications |
13.79 |
17.55 |
14.74 |
22 |
Financial services |
8.18 |
11.68 |
9.06 |
23 |
Public administration & Defence |
6.45 |
1.44 |
5.19 |
24 |
Education |
1.06 |
0.19 |
0.84 |
25 |
Health & Social work |
1.81 |
4.19 |
2.41 |
26 |
Other Services |
7.46 |
10.21 |
8.15 |
| Source: Authors’ calculations. |
To examine how growth rates for Intermediate Input in the total economy changed during the Indian growth resurgence 2000-2008vis-à-vis the earlier 1980-1999 period, a comparison has been drawn in Figure 5.1. The most striking conclusion is the huge growth in material input for the total economy after 2000. However, the growth of energy input for the total economy was faster in the first period, i.e., 1980-1999. The value of real intermediate inputs has been gradually increasing overtime for the Indian economy from 1980-2008.
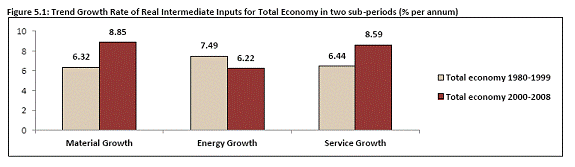
Table 5.9: Trend Growth Rate of Real Energy Input by Industry, 1980-2008 |
(% per annum) |
Industry No |
Industry Description |
1980
to
1999 |
2000
to
2008 |
1980
to
2008 |
1 |
Agriculture, Hunting, Forestry &Fishing |
1.27 |
0.29 |
1.02 |
2 |
Mining & Quarrying |
3.29 |
2.67 |
3.14 |
3 |
Food products, Beverages & Tobacco |
8.66 |
11.85 |
9.46 |
4 |
Textiles & Leather products |
3.85 |
4.83 |
4.10 |
5 |
Wood & Products of wood |
9.45 |
-4.06 |
6.05 |
6 |
Pulp, Paper, Paper products, Printing & Publishing |
6.57 |
-1.40 |
4.57 |
7 |
Coke, Refined Petroleum |
2.17 |
15.54 |
5.53 |
8 |
Chemicals & products |
5.81 |
5.87 |
5.83 |
9 |
Rubber & Plastic products |
10.44 |
-0.70 |
7.64 |
10 |
Other Non-Metallic Mineral products |
6.92 |
4.50 |
6.31 |
11 |
Basic Metals & Fabricated Metal products |
5.82 |
14.70 |
8.05 |
12 |
Machinery, nec. |
5.78 |
-0.78 |
4.13 |
13 |
Electrical & Optical equipment |
11.55 |
7.67 |
10.58 |
14 |
Transport equipment |
10.58 |
-4.85 |
6.70 |
15 |
Manufacturing, nec |
7.82 |
6.16 |
7.41 |
16 |
Electricity, Gas & Water Supply |
12.22 |
-3.47 |
8.28 |
17 |
Construction |
8.66 |
18.96 |
11.25 |
18 |
Trade |
6.33 |
3.30 |
5.57 |
19 |
Hotels & Restaurants |
3.50 |
6.96 |
4.37 |
20 |
Transport & Storage |
10.24 |
4.76 |
8.87 |
21 |
Post & Telecommunications |
15.12 |
2.93 |
12.06 |
22 |
Financial services |
10.19 |
7.16 |
9.43 |
23 |
Public administration & Defence |
1.46 |
1.89 |
1.57 |
24 |
Education |
12.14 |
-1.92 |
8.61 |
25 |
Health & Social work |
1.62 |
5.46 |
2.59 |
26 |
Other services |
5.57 |
13.43 |
7.54 |
Source: Authors’ calculations. |
Table 5.10: Trend Growth Rate of Real Service Input by Industry, 1980-2008 |
| (% per annum) |
Industry No |
Industry Description |
1980
to
1999 |
2000
to
2008 |
1980
to
2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
4.40 |
2.30 |
3.87 |
2 |
Mining & Quarrying |
4.80 |
9.03 |
5.86 |
3 |
Food products, Beverages & Tobacco |
8.00 |
10.20 |
8.55 |
4 |
Textiles & Leather products |
7.38 |
4.11 |
6.56 |
5 |
Wood & Products of wood |
5.80 |
-1.87 |
3.87 |
6 |
Pulp, Paper, Paper products, Printing & Publishing |
6.46 |
3.70 |
5.76 |
7 |
Coke, Refined Petroleum |
4.96 |
8.35 |
5.81 |
8 |
Chemicals & products |
6.65 |
6.84 |
6.69 |
9 |
Rubber & Plastic products |
7.54 |
3.12 |
6.43 |
10 |
Other Non-Metallic Mineral products |
5.91 |
5.89 |
5.90 |
11 |
Basic Metals & Fabricated Metal products |
6.56 |
11.10 |
7.70 |
12 |
Machinery, nec. |
4.06 |
3.58 |
3.94 |
13 |
Electrical & Optical equipment |
9.34 |
15.42 |
10.87 |
14 |
Transport equipment |
9.76 |
3.83 |
8.27 |
15 |
Manufacturing, nec |
5.06 |
1.30 |
4.11 |
16 |
Electricity, Gas & Water Supply |
9.87 |
2.18 |
7.94 |
17 |
Construction |
6.53 |
13.43 |
8.27 |
18 |
Trade |
0.93 |
8.28 |
2.78 |
19 |
Hotels & Restaurants |
7.92 |
13.60 |
9.35 |
20 |
Transport & Storage |
8.92 |
8.40 |
8.79 |
21 |
Post &Telecommunications |
11.41 |
8.37 |
10.65 |
22 |
Financial services |
10.22 |
11.89 |
10.64 |
23 |
Public administration &Defence |
5.93 |
5.57 |
5.84 |
24 |
Education |
9.28 |
10.77 |
9.66 |
25 |
Health & Social work |
3.09 |
1.23 |
2.62 |
26 |
Other Services |
7.43 |
8.91 |
7.80 |
Source: Authors’ calculations. |
5.5 Shares of Labour, Capital and Intermediate Inputs in Gross Output
5.5.1 Data Sources and Methodology
The distribution of income between capital and labour is an important element in growth accounting because income shares, under conditions of competitive markets, can be used to measure the contribution of each factor towards output growth. There are, however, difficulties in obtaining estimates of labour income share in value added for different sectors of the Indian economy from the available data, and this has impelled some studies to make adhoc assumptions about factor elasticities or factor income shares. Bosworth, Collins and Virmani (2007), for instance, estimate TFP growth by using certain assumed labour elasticities in the broad sectors of the economy. They assume that the elasticity of real value added with respect to labour (equal to labour income share in value added under competitive conditions) is 0.50 and 0.60 in the agricultural sector and non-agricultural sector (industry and services), respectively. Since the growth rates of labour and capital inputs differ a lot in most sectors of the Indian economy, the use of adhoc, assumed elasticities or factor shares can cause a significant bias in the estimates of TFP growth if the assumed factor shares differ from the true income shares of labour and capital. In this study, therefore, an attempt has been made to measure the labour income share series for the period from 1980 to 2008 for the 26 industries into which the economy is divided.
There are no published data on factor income shares in the Indian economy at a disaggregated level. National Accounts Statistics (NAS) of the CSO publishes the NDP series comprising compensation for employees (CE), operating surplus (OS) and mixed income (MI) for NAS industries. The income of self-employed persons, i.e., mixed income, is not separated into the labour and capital components. Therefore, to compute the share of labour income out of value added, one has to take the sum of the compensation of employees and that part of the mixed income that is wages for labour.
The computation of labour income share for the 26 study industries involves two steps. First, estimates of CE, OS and MI have to be obtained for each of the 26 industries from the NAS data, which are available only for the NAS sectors. Second, the estimate of mixed income has to be split into labour income and capital income for each industry for each year (except for industries for which the reported mixed income is zero, for instance, public administration).
Step I: Estimation of CE, OS and MI for the 26 study Industries
For some industries under study, for instance (i) Agriculture, hunting, forestry & fishing, (ii) Mining & quarrying, (iii) Electricity, gas and water supply and (iv) Construction, the required data are readily available from NAS. For others, the estimates available in NAS have to be distributed across the study industries. In certain cases, the estimates of CE, OS and MI for a particular NAS sector have been distributed across constituent study industries proportionately in accordance with the gross value added in those industries. Estimate of factor incomes for ‘other services’ in NAS , for instance, has been split into estimates for (i) Education, (ii) Health and Social Work, and (iii) Other Community, Social and Personal Services including Renting of machinery and business services, and private household with employed persons.
NAS provides estimates of factor incomes for registered manufacturing and unregistered manufacturing, but not for individual manufacturing industries. The NAS estimates of factor incomes for registered manufacturing have to be split into various manufacturing industries considered in the study (13 in number) using ASI data. The reported CE in NAS for registered manufacturing has been distributed into those 13 industries in proportion to the reported ASI data on emoluments for various industries. In a similar way, using ASI data, the estimate of OS for registered manufacturing has been distributed. Emoluments are subtracted from gross value added for various industries yielding capital income. The share of different industries in aggregate capital income of organised manufacturing indicated by the ASI data is used to split the estimate of OS for registered manufacturing reported in NAS.
The methodology applied for unregistered manufacturing is similar. The published results and unit level data of survey of unorganised manufacturing industries have been used for this purpose. The estimates of wage payments (to hired workers) in different industries have been used to split (proportionately) the estimate of CE in NAS for aggregate unregistered manufacturing. The estimated wage payment is subtracted from the estimated value added to obtain an estimate of capital income and mixed income of the self-employed in various unorganised manufacturing industries. The estimate of MI provided in NAS for unregistered manufacturing has then been proportionately distributed across industries using the estimate of capital income and mixed income of the self-employed in various industries that could be formed on the basis of published results and unit-level data from the survey of unorganised manufacturing industries.
Unlike the ASI data for organised manufacturing, the data for unorganised manufacturing enterprises are available only for select years. The proportions mentioned above could therefore be computed only for those select years. Data for four rounds have been used; these are for 45th round (1989-90), 51st round (1994-95), 56th round (2000-01) and 62nd round (2005-06). It has accordingly been necessary to resort to interpolation/ extrapolation to obtain the relevant proportions for other years.
Step II: Splitting MI into Labour Income and Capital Income
As explained above, the income share of labour is computed as:
In this equation, SLit is the labour income share in industry i in year t, CEit is compensation of employees in industry i in year t, MIit is mixed income of the self-employed persons in industry i in year t, and GVAit is gross value added in industry i in year t. The labour income proportion in mixed income is denoted by η which is taken to be a fixed parameter for each industry, not varying over time.
The derivation of the GVA series for different industries has been briefly explained in Chapter 3 of the report. The derivation of CE and MI series has been explained in Step I above. Therefore, only the estimation method of η needs to be described. The estimation of η has been done with the help of NSSO survey-based estimates of employment of different categories of workers (number of persons and days of work) and wage rates coupled with estimates of MI obtained from NAS. Two approaches have been used to get an estimate of η, and the labour income share series for different industries finally adopted in the study uses an average of the estimates of η obtained by the two approaches.
In the first approach, an estimate of labour income of self-employed workers has been made for each KLEMS industry for five years, 1983-84, 1987-88, 1993-94, 1999-00, and 2004-05 on the basis of the estimated number of self-employed, wage rate of self-employed and the number of days of work per week. These estimates, based on unit records of NSS employment-unemployment survey (major rounds), provide an estimate of the annual labour income of self-employed workers, which is divided by the mixed income of self-employed (derived from NAS) to get an estimate of η. For five industries, the ratio in question has been computed and applied. For the other 21 industries, the ratio has been computed after clubbing the industries into 11 industry groups31. In the latter case, a common ratio computed for a group of industries has then been applied to constituent industries.
In the second approach, the NSS data are used to compute the following ratio: the ratio of labour income of self-employed workers to the labour income of regular and casual workers. Let this be denoted by θ. Then, the estimate of CE provided in NAS is multiplied by θ to obtain an estimate of the labour income component out of the MI reported in NAS. The labour component of MI divided by total MI gives an estimate of η. If the estimated labour component of MI exceeds the estimate of MI, the estimate of η has been taken as unity.
The estimated labour income share out of mixed income varies significantly for the five years for which the ratio in question has been estimated. In several cases, the estimate for 1987-88 is found to be out of line with the estimates for the other four years. Therefore, while taking an average across the estimates for different years, the estimates for 1987-88 have been left out.
The estimates for η obtained by the first approach appear to be somewhat low. For the economy as a whole, the income share of labour is found to be 0.34 (on average), which suggests that in a typical enterprise of self-employed persons (family labour), the labour component of the mixed income is about 34 per cent. This does not seem right; it should be much higher. The estimated labour income share is only about 0.14 for the group containing education and health and 0.13 for the group containing miscellaneous services including financial services, real estate and business services, which does not seem plausible. These estimates are lower than what one would expect. The estimates for η obtained by the second approach, on the other hand, has the problem that in some cases the estimated labour component of MI exceeds the estimate of MI given in NAS, and therefore η is taken as one32. The estimates probably overstate the labour component out of mixed incomes for some of the industries, for instance, construction. Taking into account all these factors, an average has been taken for deriving the labour income share series.
5.5.3 Estimates of Factor Income Shares in Gross Output
The estimated factor income shares in gross output for 26 industries are presented in Table 5.11. The estimates have been made for all years in the period 1980 to 2008, and only the period averages are shown in the table.
Table 5.11: Factor Income Shares in Gross Output |
Industry No |
Industry description |
Period average 1980-81 to 2008-09 |
Energy Input |
Material Input |
Services Input |
Labour Input |
Capital Input |
1 |
Agriculture, Hunting, Forestry & Fishing |
0.012 |
0.175 |
0.043 |
0.386 |
0.384 |
2 |
Mining &Quarrying |
0.058 |
0.118 |
0.071 |
0.280 |
0.474 |
3 |
Food Products, Beverages & Tobacco |
0.022 |
0.616 |
0.188 |
0.083 |
0.092 |
4 |
Textiles, Textile Products, Leather & Footwear |
0.051 |
0.457 |
0.219 |
0.142 |
0.131 |
5 |
Wood & products of Wood |
0.019 |
0.335 |
0.119 |
0.352 |
0.175 |
6 |
Pulp, Paper, Paper Products, Printing & Publishing |
0.075 |
0.462 |
0.182 |
0.146 |
0.135 |
7 |
Coke, Refined Petroleum products & Nuclear Fuel |
0.079 |
0.686 |
0.112 |
0.016 |
0.107 |
8 |
Chemicals & Chemical products |
0.106 |
0.479 |
0.175 |
0.060 |
0.181 |
9 |
Rubber & Plastic products |
0.051 |
0.542 |
0.172 |
0.066 |
0.169 |
10 |
Other Non-Metallic Mineral products |
0.165 |
0.294 |
0.207 |
0.143 |
0.192 |
11 |
Basic Metals & Fabricated Metal products |
0.123 |
0.454 |
0.191 |
0.081 |
0.150 |
12 |
Machinery, nec |
0.033 |
0.489 |
0.173 |
0.123 |
0.183 |
13 |
Electrical & Optical equipment |
0.034 |
0.540 |
0.202 |
0.064 |
0.159 |
14 |
Transport equipment |
0.048 |
0.498 |
0.202 |
0.120 |
0.132 |
15 |
Manufacturing, nec; recycling |
0.030 |
0.481 |
0.117 |
0.167 |
0.204 |
16 |
Electricity, Gas & Water Supply |
0.172 |
0.305 |
0.162 |
0.148 |
0.212 |
17 |
Construction |
0.021 |
0.426 |
0.192 |
0.299 |
0.062 |
18 |
Trade |
0.018 |
0.030 |
0.182 |
0.290 |
0.480 |
19 |
Hotels & Restaurants |
0.043 |
0.495 |
0.146 |
0.113 |
0.204 |
20 |
Transport & Storage |
0.191 |
0.177 |
0.207 |
0.222 |
0.204 |
21 |
Post & Telecommunications |
0.024 |
0.092 |
0.062 |
0.375 |
0.446 |
22 |
Financial services |
0.015 |
0.032 |
0.155 |
0.355 |
0.443 |
23 |
Public Administration & Defence; Compulsory Social Security |
0.005 |
0.046 |
0.216 |
0.625 |
0.108 |
24 |
Education |
0.002 |
0.065 |
0.057 |
0.524 |
0.352 |
25 |
Health & Social Work |
0.010 |
0.362 |
0.144 |
0.284 |
0.200 |
26 |
Other Services |
0.006 |
0.125 |
0.058 |
0.366 |
0.445 |
Source: Authors’ Calculations. |
It is observed that intermediate input shares (mainly material input shares) are relatively high in all manufacturing industries, electricity, gas & water supply and the construction sector. Capital input share is high for mining &quarrying, and the majority of services except for education and health & social work.
It is to be noted that for the agriculture sector, the non-labour income share is further distributed into land income share and capital income share. The average cost shares for agriculture33 are 0.23 for intermediate inputs, 0.39 for labour input and 0.19 each for land and capital input.
5.6 Some Unavoidable data adjustments in database
The objective of this research project is to create a database for undertaking comparative productivity analysis. This, in turn, necessitates the construction of an industry-level dataset covering the entire Indian economy on variables such as labour, capital and intermediate inputs and output for measuring labour as well as total factor productivity. The organising principles of these datasets are those of the neoclassical growth accounting framework, yet it has to be kept in mind while interpreting these data series that the neoclassical assumptions are not always well suited for investigating certain kinds of questions about the sources of growth. In particular, assumptions of perfect competition in output and input markets, constant returns to scale, perfect information and full efficiency may not be the best set of assumptions to invoke when analysing productivity growth at the economy and industry levels in developing and emerging economies like India.
A crucial question in productivity analysis is whether the data used in the analysis are good enough to support the conclusions drawn from them. In general, productivity estimates will be biased if nominal outputs, prices, inputs or cost shares are not measured correctly (see Diewert, 2007; Schreyer, 2001). Timmer et al. (2010, Chapter 3) have explained the unresolved measurement issues in EU KLEMS, stressing, however, that the limitations of the EU KLEMS series vary widely by country, period and variables and prudent users of the data should familiarise themselves with the methods of construction as discussed on a country-by-country basis in Timmer, van Moergastel, Stuivenwold et al. (2007).
Jorgenson et al. (2005) mention many different data sources, each with its strengths and weaknesses, and these are used to varying degrees by the different studies of industry productivity for the US economy. Gordon (1999) documents the importance of these differences for productivity analysis and Bosworth and Triplett (2003) present a detailed discussion of this difference.
In this context, it is useful to highlight several data issues that bear on these productivity results; this is analogous to those explained in Jorgenson et al. (2005, Chapter 4) for the US economy and Timmer et al. (2010, Chapter 3) for the EU economy. Some limitations in the construction of input series are listed below:
(A) Data issues related to Labour:
-
The educational categories in the 38th and 43th round did not have a separate classification for higher secondary (Hr. Sec.) and was introduced for the first time in the 50th round. Hence, the categories are not exactly comparable in the five rounds. For this reason, the middle, secondary and higher secondary categories have been combined into a category of middle to higher secondary for the purpose of our analysis and the entire workforce is put into three educational groups—up to primary, middle to higher secondary and above higher secondary.
-
There are also some conceptual differences between the NSSO major rounds in the way employment and unemployment status of a person is defined.
-
The problem of concordance between NIC and KLEMS classifications is observed in the first two rounds, i.e., 38th and 43rd. While the concordance required is at 4 digits for NIC 1970, the codes used in NSSO surveys are in 3 digits, so proportional bifurcation has been done for some industries, e.g., NIC 265, 321 and 363 into two KLEMS industries. It may also be mentioned that for these rounds and the 50th round there is no complete specification of the principal and subsidiary industry for all the UPSS employed persons. It is 99.7 per cent, 97 per cent and 99.4 per cent in the 38th, 43rd and 50th rounds, respectively. Also, to maintain consistency with NAS and the earlier rounds, custom tailoring, which is included in manufacturing in the 55th and 61st rounds by the NSSO, has been included in services in these two rounds also.
(B) Data issues related to Capital:
The measures of capital service are constructed under neoclassical assumptions that equate marginal cost with prices. In addition, any limitations associated with the measurement of capital stock using the perpetual inventory method, such as the assumption of geometric depreciation rate and imputation of initial stock, are also applicable. This is because the flow of capital services is assumed to be proportional to capital stock at the individual asset level.
-
The study assumes the following asset lifetimes as provided in the NAS: 80 years for buildings, 20 years for transport equipment and 25 years for machinery and equipment. As noted before, when computing capital stock, most studies in the Indian context have either assumed zero depreciation rates, or used a common depreciation rate for the aggregates of all assets, i.e., the total capital stock. These common depreciation rates hover around 5 to 6 per cent (e.g., Bosworth and Collins, 2008; Goldar, 1986a). Since different depreciation rates, have been used in this study, for different asset types, derived using double declining balance rate, there is no aggregate depreciation rate. However, the implicit aggregate depreciation rate has been derived, which is a weighted depreciation rate of individual assets, as δt=1-[(St- It)/ St-1], with δ being the rate of depreciation, S and I are capital stock and Investment in year t. The derived rates vary across industries and over time, due to changes in the asset composition. The overall depreciation rate for the entire period is about 4 per cent, with agriculture showing the lowest at 3 per cent and manufacturing showing the highest at 6 per cent. These rates are low compared to those in many previous aggregate studies in the context of India (Bosworth and Collins, 2008). Also, at the individual asset level, the assumed depreciation rates are lower than those in many cross-country studies and databases (e.g., Easterly and Levine, 2001; Penn World Tables, EU KLEMS). There are divergent views on whether the lifetime of capital in developing countries is different from that in richer countries. It may be longer as the maintenance cost in developing countries will be lower (Summers and Heston, 1995). On the other hand, it could be shorter due to under-maintenance or low efficacy of public investment (Bu, 2004; Pritchett, 2000). In any case, the assumed low depreciation might overestimate the measure of capital input growth rate. This issue will be addressed in further revisions of the data.
-
It is assumed that capital stock consists of machinery, transport equipment and construction, thereby excluding land as an input. This has been done to create a NAS (CSO)-consistent capital series, as land is excluded in the construction of capital stock by the CSO. It is, however, acknowledged that for the agriculture sector, even though some studies (e.g., Bosworth and Collins, 2008) have found the contribution of land to aggregate growth to be negligible, land may still be an important input to consider.
-
Study has used NAS deflators for machinery, transport and construction separately. In the case of ICT assets (economy level), the study has adopted the harmonisation procedure suggested by Schreyer (2002) where US hedonic deflators are adjusted for India’s domestic inflation rates.
While calculating the user cost of capital, the study has used an external (ex ante) rate of return based on market interest rate. While the external rate is free from any neoclassical assumptions, it does not assure complete consistency with national accounts. Therefore, it would be worth investigating the sensitivity of measured capital service growth rates to the choice of alternative rates of returns.
(C) Data issues related to Intermediate Inputs:
For an analysis of the use of intermediate inputs in production, it is important to note that series of energy, material and services (EMS) are derived by using their shares in intermediate inputs from input-output transaction tables applied to a series of intermediate inputs from the National Accounts. The first basic measurement issue is that the annual GDP data are not consistent with the benchmark input-output tables from the official NAS. Second, the benchmark input-output tables are not perfectly consistent overtime. The Input Flow Matrix at factor cost, published by the CSO for 1978, is a 60 x 60 matrix. The absorption matrices for 1983, 1989, 1993 and 1998 have 115 sectors. However a detailed 130-sector absorption (commodity x industry) matrix for the Indian economy has been published for 2003-04. Therefore, the old tables have been adjusted to the new. Third, input-output transaction tables are generally available at five-year intervals and this necessitates interpolation and assumption of constant shares in some cases to construct the entire time series of EMS from 1980 to 2008. Fourth, unlike studies using detailed survey data, the study had to assume that all buyers pay the same price for each commodity because there is no information about price divergences.
For certain sectors, there are huge year-to-year fluctuations in intermediate inputs, especially in energy and service inputs. This is primarily because, in certain IOTT years, there is an abrupt increase or decrease in the proportion of an input going into an industry. Therefore, such fluctuations have been smoothened by excluding the particular year in which there is an unusually high/low IOTT Input proportion going into an industry’s production process. The sectors where such adjustment has been done are as follows: Textiles & products, Leather & Footwear, Wood & Products, Machinery, nec, Manufacturing, nec; recycling, Electricity, gas &water supply, Trade, Health & Social Work, Public Administration & Defence; Compulsory social security, Education and Other Services.
-
The estimated time series of intermediate inputs at constant prices will not be consistent with the estimated gross output series at constant prices, i.e., the deflated value of intermediate input cannot match the gap between value added and gross output at constant price. This is because NAS uses a single deflation method to estimate Gross Value Added and Gross Output at constant prices.
‘E + M + S’ at Constant Price ≠ ‘GVO – GVA’ at Constant Price
However, for one sector—Agriculture—the gross output and gross value added estimated by NAS is double deflated. Therefore, only for the agriculture sector the deflated value of intermediate input will exactly match the gap between value added and gross output at constant prices.
-
There has been some confusion in the literature on the price concept to be used for intermediate inputs. It is generally acknowledged that intermediate input weights should be measured from the user’s point of view, i.e., reflect the marginal cost paid by the user. Most studies maintain that purchaser’s price should be used. These prices include net taxes on commodities paid by the user and include margins on trade and transportation (see, for example, OECD, 2001). However when trade and transportation services are included as separate intermediate inputs, margins paid on other products should also be allocated to these services. Ideally a distinction should be made between the intermediate product valued at purchaser’s price minus margins and the trade and transportation services valued at margins. This is the approach taken in Jorgenson, Gollop and Fraumeni (1987) and in Jorgenson et al. (2005). However Timmer et al. (2010, Chapter 3) explain that for the EU KLEMS database, intermediate inputs have been valued at purchaser’s price owing to unavailability of necessary data. Because of the use of the purchaser’s price concept, the shares of services in intermediate inputs do not include trade and transportation margins. Similarly, in practice for our database, the time series of Intermediate Input constructed is at purchaser’s price, i.e., it implicitly takes into account the net indirect taxes. The distribution of this net indirect tax between material, energy and services has not been possible because of unavailability of a time series of tax matrix from 1980 to 2008.
Chapter 6: Estimates of Productivity Growth for Individual Industries
6.1 Introduction
The objective of this chapter is to examine the growth performance of the individual industrial sectors of the Indian economy for the period 1980-2008 and to understand the proximate sources of growth.
The layout of the chapter is as follows: Section 6.2 provides estimates of labour productivity growth for the 26 industrial sectors of the economy. In Section 6.3, the total factor productivity estimates for the industries using both value added and gross output framework is provided. The sources of output growth are examined in the next section using the two-input (KL) as well as the five-input (KLEMS) framework. Section 6.5 explains the growth acceleration during the phase 2000-08 over 1980-99. The final section summarises our findings.
6.2 Estimates of Labour Productivity Growth
The contribution to labour productivity growth comes from four sources: capital deepening where more or better capital makes labour more productive; labour quality or labour compositional changes; contribution of intermediate input deepening, which reflects the impact of more intermediate-intensive production on labour productivity; and finally from TFP growth, which contributes to labour productivity point-for-point (Jorgensen, 2005)34.
6.2.1 Growth of Labour Productivity
There has been a substantial structural shift of the labour force from the primary sector (where its employment share was 68 per cent in 1983 and only 51.3 per cent in 2009-10) to services (where the employment share increased from 17.6 per cent to 26.7 per cent during the same period).This has, however, not been commensurate with changes in sectoral share in GDP. While the share of the primary sector in GDP reduced from 37 per cent to 15.2 per cent, the share of services increased from 38.6 per cent to 58.8 per cent over the same period. It, thus, reflects how per worker productivity has changed over the period.
The labour productivity growth rates are presented for the 26 sectors in Table 6.1. It shows that the growth rates vary widely across the industries for the given periods.
The agriculture sector recorded around 2 per cent growth in labour productivity for the entire period, though it experienced acceleration during 2000 to 2008. In the recent period substantial improvements in labour productivity growth have also been noticed in construction and some of the manufacturing and services sectors.
Table 6.1: Growth Rate of Labour Productivity, 1980 to 2008 |
(% per annum) |
Industry
No. |
Industry Description |
1980
to
1999 |
2000
to
2008 |
1980
to
2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
1.72 |
2.59 |
1.94 |
2 |
Mining & Quarrying |
3.88 |
2.54 |
3.54 |
3 |
Food Products, Beverages & Tobacco |
2.99 |
8.86 |
4.47 |
4 |
Textiles & Leather products |
7.01 |
2.25 |
5.81 |
5 |
Wood & Products of wood |
–0.89 |
–4.25 |
–1.74 |
6 |
Pulp, Paper & Paper products, printing & publishing |
2.92 |
1.11 |
2.47 |
7 |
Coke, Refined Petroleum products & Nuclear fuel |
–3.36 |
15.41 |
1.35 |
8 |
Chemicals & Chemical products |
4.57 |
8.13 |
5.47 |
9 |
Rubber & Plastic products |
2.11 |
10.24 |
4.15 |
10 |
Other Non-Metallic Mineral products |
6.56 |
3.56 |
5.80 |
11 |
Basic Metals & Fabricated Metal products |
3.51 |
9.96 |
5.13 |
12 |
Machinery, nec. |
–1.48 |
3.59 |
–0.21 |
13 |
Electrical & Optical equipment |
6.12 |
14.16 |
8.14 |
14 |
Transport equipment |
7.60 |
–2.97 |
4.95 |
15 |
Manufacturing, nec |
7.33 |
4.56 |
6.63 |
16 |
Electricity, Gas & Water Supply |
6.17 |
5.42 |
5.98 |
17 |
Construction |
–0.31 |
3.77 |
0.72 |
18 |
Trade |
1.34 |
5.86 |
2.47 |
19 |
Hotels & Restaurants |
3.38 |
6.33 |
4.12 |
20 |
Transport & Storage |
2.44 |
4.98 |
3.08 |
21 |
Post & Telecommunications |
3.88 |
21.41 |
8.29 |
22 |
Financial services |
5.06 |
5.70 |
5.22 |
23 |
Public Administration & Defence |
4.38 |
6.75 |
4.98 |
24 |
Education |
3.16 |
2.44 |
2.98 |
25 |
Health & Social work |
1.24 |
1.88 |
1.40 |
26 |
Other services |
2.24 |
3.88 |
2.65 |
Note: Labour productivity is here defined as real gross output per person employed.
Source: Authors’ calculations. |
6.2.2 Sources of Growth in Labour Productivity
The contribution of the four sources of growth in labour productivity for the 26 sectors for the period 1980 to 2008 is presented in Table 6.2. It is evident that across the 26 sectors the median contribution of intermediate inputs is 1.8 percentage points out of 4.1 percent, followed by 1.1 percentage points by capital deepening, 0.33 percentage points by TFP and 0.13 percentage points by labour composition index. In 17 of the 26 industrial sectors, intermediate input deepening contributed the maximum to labour productivity; in three industries TFP contributed the maximum and only in six industries capital deepening contributed the maximum to labour productivity. In all the sectors the contribution of labour composition growth has been quite marginal, the median being 0.13 per cent except in mining, post & telecommunications, public administration, education and other services.
Table 6.2: Sources of Labour Productivity Growth, 1980 to 2008 |
| (% per annum) |
Industry No |
Industry Description |
Contribution of Labour Composition |
Contribution of capital service per person employed |
Contribution of intermediate Inputs per person employed |
Contribution of TFPG |
Labour Productivity Growth |
1 |
Agriculture, Hunting, Forestry & Fishing |
0.10 |
1.04 |
0.32 |
0.48 |
1.94 |
2 |
Mining & Quarrying |
0.30 |
2.27 |
1.17 |
–0.20 |
3.54 |
3 |
Food products, Beverages & Tobacco |
0.07 |
0.44 |
4.11 |
–0.15 |
4.47 |
4 |
Textiles, Textile products, Leather & Footwear |
0.12 |
1.28 |
4.17 |
0.24 |
5.81 |
5 |
Wood & Products of Wood |
0.01 |
1.54 |
0.94 |
–4.23 |
–1.74 |
6 |
Pulp, Paper, Paper Products, Printing & Publishing |
0.15 |
0.47 |
1.87 |
–0.02 |
2.47 |
7 |
Coke, Refined Petroleum products & Nuclear Fuel |
0.01 |
0.92 |
1.72 |
–1.30 |
1.35 |
8 |
Chemicals & Chemical products |
0.07 |
1.39 |
3.95 |
0.06 |
5.47 |
9 |
Rubber & Plastic products |
0.07 |
1.04 |
3.27 |
–0.23 |
4.15 |
10 |
Other Non-Metallic Mineral products |
0.11 |
1.37 |
3.91 |
0.41 |
5.80 |
11 |
Basic Metals & Fabricated Metal products |
0.03 |
1.12 |
3.43 |
0.55 |
5.13 |
12 |
Machinery, nec |
0.22 |
0.08 |
–0.02 |
–0.50 |
–0.21 |
13 |
Electrical & Optical equipment |
0.03 |
0.66 |
6.37 |
1.08 |
8.14 |
14 |
Transport equipment |
0.09 |
1.13 |
3.30 |
0.42 |
4.95 |
15 |
Manufacturing, nec; recycling |
0.14 |
1.31 |
3.88 |
1.31 |
6.63 |
16 |
Electricity, Gas & Water Supply |
0.12 |
1.12 |
3.52 |
1.22 |
5.98 |
17 |
Construction |
0.13 |
0.18 |
1.59 |
–1.18 |
0.72 |
18 |
Trade |
0.23 |
0.82 |
–0.21 |
1.64 |
2.47 |
19 |
Hotels & Restaurants |
0.06 |
0.60 |
2.67 |
0.79 |
4.12 |
20 |
Transport & Storage |
0.16 |
0.50 |
2.54 |
–0.13 |
3.08 |
21 |
Post & Telecommunications |
0.19 |
1.93 |
1.21 |
4.97 |
8.29 |
22 |
Financial Services |
0.17 |
3.15 |
1.12 |
0.78 |
5.22 |
23 |
Public Administration & Defence |
0.39 |
0.42 |
1.36 |
2.81 |
4.98 |
24 |
Education |
0.34 |
2.29 |
0.15 |
0.20 |
2.98 |
25 |
Health & Social Work |
0.25 |
1.61 |
–0.39 |
–0.06 |
1.40 |
26 |
Other Services |
0.41 |
0.45 |
0.82 |
0.97 |
2.65 |
|
Median |
0.13 |
1.08 |
1.80 |
0.33 |
4.14 |
| Source: Authors’ calculations. |
6.3 Estimates of Total Factor Productivity growth at the Industry Level
6.3.1 Estimates of TFP using a Value Added Framework
Table 6.3 presents the estimates of total factor productivity growth for the period 1980-2008 using measures of labour and capital defined as labour input and capital stock. The last column presents evidence on productivity growth for the same 26 industries of the Indian economy using a different measure of capital-capital services.
It is observed that both estimates of productivity show wide inter-industry variations. The changes in the asset composition of capital stock, i.e., the increasing share of equipment, have been a source of output growth in different sectors of the economy. The conventional measure of capital input based on the aggregate stock of capital assets tends to attribute this component of growth to the productivity residual, whereas it is actually attributable to capital input, and more specifically to the gains in capital productivity that arise from changes in the composition of capital assets.
The industries belonging to the services sector show a higher rate of productivity growth compared with the other sectors. Also, reforms in the mid-1980s as well as in the early 1990s were specifically targeted to improve competitiveness and productivity in this sector.
Comparison of TFP growth between sub-periods
Table 6.3 also reports the growth of TFP for each industry for the two sub-periods 1980-1999 and 2000-2008. The median TFP growth rate has increased for the 26 industries from 0.33 per cent for 1980-99 to 0.69 per cent for the period 2000-08. The mean growth rates are substantially higher due to rapid TFP growth in some of the industries.
6.3.2 Estimates of TFP using a Gross Output Framework
The study has considered three intermediate inputs—energy, material and services—as intermediate inputs are the primary component of some industries’ output35. Our measure of labour input incorporates the qualitative aspects of the labour force and the capital input is defined in terms of capital service that takes into account the asset heterogeneity aspects. Table 6.4 presents the estimates of productivity growth for the period 1980-2008.
Comparison of TFP growth between sub-periods
Table 6.4 reports the growth of TFP for each industry for the full period 1980-2008 and the two sub-periods 1980-1999 and 2000-2008.
The median growth rate has increased sharply for the 26 industries from 0.13 per cent for 1980-99 to 0.63 per cent for the period 2000-08, though there are wide fluctuations in TFP growth rates across industries.
Table 6.3: Trend Growth Rate of Total Factor Productivity using a Value added framework:
26 Industries, 1980-2008 |
(% per annum) |
Industry No |
Industry Description |
GVA
Growth
|
TFPG* |
TFPG** |
TFPG**
1980 To 1999 |
TFPG**
2000 To 2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
2.96 |
1.65 |
1.49 |
1.77 |
0.67 |
2 |
Mining & Quarrying |
5.3 |
0.38 |
0.3 |
0.42 |
–0.05 |
3 |
Food products, Beverages & Tobacco |
5.68 |
1.26 |
0.86 |
0.11 |
3.11 |
4 |
Textiles & Leather products |
5.29 |
–0.22 |
–0.47 |
–0.11 |
–1.56 |
5 |
Wood & products of wood |
–1.9 |
–5.44 |
–5.53 |
–5.46 |
–5.73 |
6 |
Pulp, Paper, Paper products, printing & publishing |
5.07 |
0.27 |
–0.34 |
0.24 |
–2.08 |
7 |
Coke, Refined Petroleum products & Nuclear fuel |
7.86 |
–2.09 |
–2.89 |
–2.85 |
–3.01 |
8 |
Chemicals & Chemical products |
8.72 |
0.61 |
0.17 |
–0.30 |
1.56 |
9 |
Rubber & Plastic products |
7.84 |
–1.95 |
–2.42 |
–4.39 |
3.48 |
10 |
Other Non-Metallic Mineral products |
6.97 |
1.76 |
0.72 |
0.72 |
0.71 |
11 |
Basic Metals & Fabricated Metal products |
6.68 |
–0.22 |
–0.75 |
–2.02 |
3.05 |
12 |
Machinery, nec. |
3.88 |
–1.29 |
–1.71 |
–2.36 |
0.22 |
13 |
Electrical & Optical equipment |
7.8 |
1.42 |
0.48 |
–0.87 |
4.52 |
14 |
Transport equipment |
7.11 |
–0.41 |
–0.82 |
–0.35 |
–2.24 |
15 |
Manufacturing, nec |
6.92 |
–0.36 |
–0.18 |
0.87 |
–3.32 |
16 |
Electricity, Gas & Water Supply |
6.86 |
2.04 |
2.01 |
2.14 |
1.64 |
17 |
Construction |
6.03 |
–0.76 |
–0.76 |
–0.99 |
–0.07 |
18 |
Trade |
7.04 |
2.28 |
2.02 |
2.18 |
1.53 |
19 |
Hotels & Restaurants |
8.44 |
2.87 |
2.59 |
2.22 |
3.7 |
20 |
Transport & Storage |
6.46 |
0.84 |
0.73 |
0.63 |
1 |
21 |
Post & Telecommunications |
13.9 |
5.83 |
5.49 |
0.93 |
19.09 |
22 |
Financial services |
9.61 |
1.29 |
0.95 |
–1.05 |
6.91 |
23 |
Public Administration & Defence |
5.63 |
3.95 |
3.94 |
3.42 |
5.48 |
24 |
Education |
7.27 |
0.28 |
0.25 |
1.31 |
–2.91 |
25 |
Health & Social Work |
7.69 |
0.56 |
0.53 |
1.66 |
–2.83 |
26 |
Other services |
6.35 |
1.39 |
1.23 |
2.06 |
–1.25 |
|
Industry Mean |
6.6 |
0.61 |
0.3 |
-0.003 |
1.216 |
|
Industry Median |
6.89 |
0.59 |
0.39 |
0.33 |
0.69 |
Note: In TFP estimates of Agriculture sector, land is taken as an input.
* TFP Growth computed using Labour input and K stock.
** TFP Growth computed using Labour input and K service.
Source: Authors’ calculations. |
Table 6.4: Trend Growth Rate of Total Factor Productivity using a Gross Output Framework:
26 Industries, 1980-2008 |
(% per annum) |
Industry No |
Industry Description |
GVO Growth |
TFPG* |
TFPG** |
TFPG* 1980 to 1999 |
TFPG** 2000 to 2008 |
1 |
Agriculture, Hunting, Forestry & Fishing |
2.82 |
1.29 |
1.17 |
1.37 |
0.58 |
2 |
Mining & Quarrying |
5.08 |
–0.15 |
–0.20 |
0.15 |
–1.24 |
3 |
Food Products, Beverages & Tobacco |
6.38 |
–0.08 |
–0.15 |
–0.08 |
–0.38 |
4 |
Textiles & Leather Products |
6.45 |
0.31 |
0.24 |
0.1 |
0.67 |
5 |
Wood & Products of wood |
–1.09 |
–4.18 |
–4.23 |
–4.57 |
–3.21 |
6 |
Pulp, Paper, Paper products, printing & publishing |
5.72 |
0.15 |
–0.02 |
0.08 |
–0.30 |
7 |
Coke, Refined Petroleum products & Nuclear fuel |
5.42 |
–1.19 |
–1.30 |
–0.64 |
–3.27 |
8 |
Chemicals & Chemical Products |
8.06 |
0.16 |
0.06 |
–0.19 |
0.78 |
9 |
Rubber & Plastic Products |
9.45 |
–0.12 |
–0.23 |
–0.60 |
0.88 |
10 |
Other Non-Metallic Mineral Products |
7.66 |
0.76 |
0.41 |
0.57 |
–0.04 |
11 |
Basic Metals & Fabricated Metal Products |
7.56 |
0.67 |
0.55 |
–0.53 |
3.77 |
12 |
Machinery, nec. |
4.28 |
–0.38 |
–0.50 |
–0.65 |
–0.05 |
13 |
Electrical & Optical Equipment |
12.18 |
1.31 |
1.08 |
0.92 |
1.56 |
14 |
Transport Equipment |
7.86 |
0.52 |
0.42 |
–0.01 |
1.72 |
15 |
Manufacturing, nec |
9.75 |
1.26 |
1.31 |
2.27 |
–1.57 |
16 |
Electricity, Gas & Water Supply |
7.38 |
1.23 |
1.22 |
0.55 |
3.24 |
17 |
Construction |
6.68 |
–1.18 |
–1.18 |
–1.49 |
–0.27 |
18 |
Trade |
6.22 |
1.85 |
1.64 |
1.8 |
1.16 |
19 |
Hotels & Restaurants |
7.89 |
0.87 |
0.79 |
0.67 |
1.12 |
20 |
Transport & Storage |
7.25 |
–0.08 |
–0.13 |
–0.62 |
1.35 |
21 |
Post & Telecommunications |
14.16 |
5.25 |
4.97 |
0.34 |
18.75 |
22 |
Financial Services |
9.87 |
1.06 |
0.78 |
–0.79 |
5.45 |
23 |
Public Administration & Defence |
5.57 |
2.82 |
2.81 |
2.43 |
3.92 |
24 |
Education |
7.02 |
0.23 |
0.2 |
1.12 |
–2.55 |
25 |
Health & Social Work |
4.94 |
–0.05 |
–0.06 |
0.2 |
–0.85 |
26 |
Other services |
6.65 |
1.1 |
0.97 |
1.79 |
–1.46 |
|
Industry Mean |
6.97 |
0.52 |
0.41 |
0.16 |
1.14 |
|
Industry Median |
6.85 |
0.42 |
0.33 |
0.13 |
0.63 |
Note: In the TFP estimates of Agriculture, land is taken as an input.
* TFP Growth computed using Labour input, K stock and Intermediate inputs.
** TFP Growth computed using Labour input, K service and Intermediate inputs.
Source: Authors’ calculations. |
6.4 Sources of Output Growth: 1980-2008
In this section, the sources of the observed output growth for each of the 26 industries of the Indian economy are accounted.
6.4.1 Gross Value Added Framework
Table 6.5 provides the breakdown of value added growth in terms of quality and quantity components for labour and capital inputs. The quantity component reflects increases in the number of units, while the quality component captures substitution towards heterogeneous inputs with relatively higher marginal products, such as a computer or a university-educated worker.
It is observed that capital input measured in terms of capital services makes a bigger contribution to value added growth across the majority of industries than capital stock. In terms of labour, it is found that labour persons dominate labour quality in 24 of the 26 industries. There are only two industries, namely, textiles and public administration & defence, where the contribution of labour composition exceeds the contribution made by labour persons.
6.4.2 KLEMS Framework
Table 6.6 presents the decomposition of output growth for the period 1980-2008 for the full set of 26 industries. The first column gives the output growth, the other columns give the contributions of the factor inputs—labour, capital, material, energy and services—and the final column provides TFP growth. It is observed that material input is the dominant source of growth for the majority of industries. In terms of median growth rate of 6.85 per cent for these 26 industries, the typical contributions from the factor inputs were as follows: contribution from intermediate material input was 2.53 percentage points, followed by capital (1.52 percentage points), labour (0.55 percentage points), energy (0.22 percentage points) and services (1.16 percentage points). For the 26 industries, the median value of TFP growth was 0.33 per cent per year. In comparison to the input contributions, TFP is the single most dominant source of industry output growth in only two industries: post & telecommunications and public administration & defence.
Table 6.5: Contribution of factor inputs and TFP to GVA Growth at industry level, 1980-2008 |
(% per annum) |
Industry Description |
GVA growth |
Contribution of Capital stock |
Contribution of Capital Quality |
Contribution of Labour Person |
Contribution of Labour Quality |
TFPG * |
TFPG** |
1 |
Agriculture, Hunting, Forestry & Fishing |
2.96 |
0.74*** |
0.16 |
0.44 |
0.13 |
1.65 |
1.49 |
2 |
Mining & Quarrying |
5.3 |
4.00 |
0.07 |
0.53 |
0.39 |
0.38 |
0.30 |
3 |
Food products, Beverages & Tobacco |
5.68 |
3.09 |
0.40 |
0.95 |
0.38 |
1.26 |
0.86 |
4 |
Textiles & Leather products |
5.29 |
4.68 |
0.25 |
0.40 |
0.44 |
–0.22 |
–0.47 |
5 |
Wood & products of wood |
–1.9 |
3.47 |
0.09 |
0.03 |
0.02 |
–5.44 |
–5.53 |
6 |
Pulp, Paper, Paper products, printing & publishing |
5.07 |
2.64 |
0.61 |
1.65 |
0.52 |
0.27 |
–0.34 |
7 |
Coke, Refined Petroleum products & Nuclear fuel |
7.86 |
9.29 |
0.80 |
0.56 |
0.11 |
–2.09 |
–2.89 |
8 |
Chemicals & Chemical products |
8.72 |
7.06 |
0.44 |
0.74 |
0.31 |
0.61 |
0.17 |
9 |
Rubber & Plastic products |
7.84 |
7.90 |
0.47 |
1.58 |
0.31 |
–1.95 |
–2.42 |
10 |
Other Non-Metallic Mineral products |
6.97 |
4.11 |
1.04 |
0.76 |
0.34 |
1.76 |
0.72 |
11 |
Basic Metals & Fabricated Metal products |
6.68 |
5.92 |
0.53 |
0.86 |
0.13 |
–0.22 |
–0.75 |
12 |
Machinery, nec. |
3.88 |
2.60 |
0.42 |
1.80 |
0.77 |
–1.29 |
–1.71 |
13 |
Electrical & Optical equipment |
7.8 |
5.05 |
0.94 |
1.16 |
0.17 |
1.42 |
0.48 |
14 |
Transport equipment |
7.11 |
5.97 |
0.41 |
1.16 |
0.39 |
–0.41 |
–0.82 |
15 |
Manufacturing, nec |
6.92 |
5.52 |
–0.17 |
1.39 |
0.37 |
–0.36 |
–0.18 |
16 |
Electricity, Gas & Water Supply |
6.86 |
3.69 |
0.02 |
0.81 |
0.32 |
2.04 |
2.01 |
17 |
Construction |
6.03 |
1.52 |
0.00 |
4.92 |
0.35 |
–0.76 |
–0.76 |
18 |
Trade |
7.04 |
3.03 |
0.26 |
1.43 |
0.29 |
2.28 |
2.02 |
19 |
Hotels & Restaurants |
8.44 |
4.02 |
0.27 |
1.38 |
0.18 |
2.87 |
2.59 |
20 |
Transport & Storage |
6.46 |
3.06 |
0.11 |
2.18 |
0.38 |
0.84 |
0.73 |
21 |
Post & Telecommunications |
13.9 |
5.59 |
0.34 |
2.27 |
0.23 |
5.83 |
5.49 |
22 |
Financial Services |
9.61 |
5.99 |
0.34 |
2.12 |
0.21 |
1.29 |
0.95 |
23 |
Public Administration & Defence |
5.63 |
0.67 |
0.02 |
0.49 |
0.53 |
3.95 |
3.94 |
24 |
Education |
7.27 |
4.20 |
0.04 |
2.40 |
0.39 |
0.28 |
0.25 |
25 |
Health & Social Work |
7.69 |
4.56 |
0.03 |
2.04 |
0.53 |
0.56 |
0.53 |
26 |
Other services |
6.35 |
2.57 |
0.16 |
1.88 |
0.52 |
1.39 |
1.23 |
Note: * TFP Growth computed using Labour input and K stock.
** TFP Growth computed using Labour input and K service.
***Includes contribution of land.
Source: Authors’ calculations. |
Table 6.6: Sources of Gross Output Growth, 1980-2008 |
| (% per annum) |
Industry No. |
Industry description |
GVO Growth |
Contribution of Labour Input |
Contribution of Capital Service |
Contribution of Material Input |
Contribution of Energy Input |
Contribution of Service Input |
TFPG * |
1 |
Agriculture, Hunting, Forestry & Fishing |
2.82 |
0.44 |
0.69** |
0.34 |
0.01 |
0.17 |
1.17 |
2 |
Mining & Quarrying |
5.08 |
0.70 |
3.03 |
0.96 |
0.18 |
0.41 |
–0.20 |
3 |
Food Products, Beverages & Tobacco |
6.38 |
0.24 |
0.62 |
3.81 |
0.21 |
1.65 |
–0.15 |
4 |
Textiles, Textile Products, Leather & Footwear |
6.45 |
0.22 |
1.34 |
3.01 |
0.21 |
1.43 |
0.24 |
5 |
Wood & Products of Wood |
–1.09 |
0.00 |
1.86 |
0.73 |
0.09 |
0.47 |
–4.23 |
6 |
Pulp, Paper, Paper Products, Printing & Publishing |
5.72 |
0.60 |
0.91 |
2.84 |
0.34 |
1.05 |
–0.02 |
7 |
Coke, Refined Petroleum Products & Nuclear Fuel |
5.42 |
0.08 |
1.36 |
4.18 |
0.41 |
0.69 |
–1.30 |
8 |
Chemicals & Chemical Products |
8.06 |
0.24 |
1.82 |
4.15 |
0.60 |
1.18 |
0.06 |
9 |
Rubber & Plastic Products |
9.45 |
0.45 |
1.94 |
5.76 |
0.37 |
1.15 |
–0.23 |
10 |
Other Non-Metallic Mineral Products |
7.66 |
0.36 |
1.72 |
2.89 |
1.04 |
1.23 |
0.41 |
11 |
Basic Metals & Fabricated Metal Products |
7.56 |
0.23 |
1.49 |
2.76 |
1.05 |
1.47 |
0.55 |
12 |
Machinery, nec |
4.28 |
0.77 |
0.91 |
2.29 |
0.13 |
0.68 |
–0.50 |
13 |
Electrical & Optical Equipment |
12.18 |
0.33 |
1.41 |
6.78 |
0.38 |
2.21 |
1.08 |
14 |
Transport Equipment |
7.86 |
0.38 |
1.55 |
3.51 |
0.31 |
1.69 |
0.42 |
15 |
Manufacturing, nec; recycling |
9.75 |
0.66 |
1.98 |
5.03 |
0.23 |
0.54 |
1.31 |
16 |
Electricity, Gas & Water Supply |
7.38 |
0.41 |
1.33 |
1.71 |
1.41 |
1.30 |
1.22 |
17 |
Construction |
6.68 |
1.91 |
0.55 |
3.55 |
0.24 |
1.60 |
–1.18 |
18 |
Trade |
6.22 |
1.32 |
2.59 |
0.14 |
0.10 |
0.43 |
1.64 |
19 |
Hotels & Restaurants |
7.89 |
0.50 |
1.37 |
3.65 |
0.18 |
1.40 |
0.79 |
20 |
Transport & Storage |
7.25 |
1.09 |
1.34 |
1.48 |
1.61 |
1.85 |
–0.13 |
21 |
Post & Telecommunications |
14.16 |
2.07 |
4.91 |
1.25 |
0.28 |
0.68 |
4.97 |
22 |
Financial Services |
9.87 |
1.87 |
5.18 |
0.26 |
0.14 |
1.64 |
0.78 |
23 |
Public Administration & Defence |
5.57 |
0.74 |
0.50 |
0.25 |
0.01 |
1.27 |
2.81 |
24 |
Education |
7.02 |
2.46 |
3.74 |
0.04 |
0.02 |
0.56 |
0.20 |
25 |
Health & Social Work |
4.94 |
1.28 |
2.39 |
0.91 |
0.03 |
0.39 |
–0.06 |
26 |
Other Services |
6.65 |
1.95 |
2.17 |
1.04 |
0.05 |
0.47 |
0.97 |
|
Industry Mean |
6.97 |
0.82 |
1.87 |
2.44 |
0.37 |
1.06 |
0.41 |
|
Industry Median |
6.85 |
0.55 |
1.52 |
2.53 |
0.22 |
1.16 |
0.33 |
Note: * TFP Growth computed using Labour input, K service and Intermediate inputs.
** Includes contribution of Land input.
Source: Authors’ calculations. |
6.5 Growth Acceleration: 2000-2008 over 1980-1999
It is also important to see how the industries performed in the sub-periods 1980-1999 and 2000-2008. A comparison of the two sub-periods indicates that there was, by and large, an improvement in industries comprising the services sector in the period 2000-2008. In manufacturing industries, food products & beverages, textiles & leather, chemicals, basic metals and electronic equipment showed impressive growth rates in the period 2000-2008.
In accounting for acceleration in output growth in the 2000s for the top 5 performers—post &telecommunications, construction, basic & fabricated metals, hotels & restaurants, electrical & optical equipment—a mixture of improvements in productivity and input accumulation is found. For post & telecommunications and basic & fabricated metal products, productivity growth seems to account for a large part of the growth acceleration in the period 2000-2008.
Finally, the study explores the changing pattern of industry-level TFP growth during the phase of growth acceleration, i.e., from 2003-04 to 2007-08. The notable observation here is that the improvement in TFP growth after 1999 is not limited to a few industries. Of the 26 industries, more than 50 per cent showed faster TFP growth during the period 2000-08 than during 1980-99. During the period 2000-08, post & telecommunications, financial services, administration & defence, basic metals and electricity, gas & water recorded more than 3 per cent TFP growth rates, while other services, manufacturing nec, education, wood & wood products and coke & petroleum emerged as the sectors with the highest negative TFP growth. This calls for a detailed examination of both TFP growth of manufacturing and services to understand what acts as an impediment to widespread productivity revival for the Indian economy and, in turn, what drives growth in the Indian economy.
6.6 Productivity Growth in Individual Industries: Manufacturing versus Services
It is now common knowledge that growth in the Indian economy has been driven by the services sector. Our industry-level estimates of TFP growth, however, indicate that productivity growth revival that began in 2000 encompasses several manufacturing industries. Eight of the 14 manufacturing industries showed faster TFP growth during the period 2000-08.Linking the improved performance in TFP to policy changes is difficult, as industrial and trade policy changes are implemented at different points of time across industries.
It can be seen that the performance of manufacturing industries in terms of TFP growth lags behind those of individual industries in the services sector. However, given that unorganised manufacturing is a large part of the overall manufacturing sector in India, any assessment of the manufacturing sector’s productivity growth would be incomplete without decomposition of the overall manufacturing TFP performance in terms of organised and unorganised segments. Further, given that unorganised manufacturing accounts for a relatively large share of employment, the improvements in productivity in unorganised segment assume tremendous significance from the policy perspective. The service industries, on the other hand, show impressive growth performance, although the sustainability of the service sector could be an issue going forward.
6.7 Summary and Conclusions
Our estimates of productivity—both labour productivity (LP) as well as TFP growth—at the 26-industry level under both the value added as well as the gross output framework show wide inter-industry variations as well as fluctuations over time. Most of the industries recorded negligible TFP growth for the period 1980-2008.Further, the evidence clearly shows that factor input accumulation accounts for the bulk of the growth across all industries, be it manufacturing or services, for the period 1980-2008. From 2000 onwards, a revival of productivity growth in several industries is found, which indicates that nearly two decades of policy reforms, especially in areas of trade and industry, seem to have made a difference.
Appendix 6A: Estimation of TFP in Agriculture
Construction of Time Series on Land Input36
This section describes the method for estimating time series of land input for agricultural use.
To arrive at the estimates of time series for land input, two definitions have been adopted. According to the first approach, land for agricultural use is defined as net area sown and fallow lands. Fallow lands include all lands that are temporarily out of cultivation for a period not less than one year and not more than five years. This definition of land for agricultural use has been adopted by Shukla and Dholakia. The land use statistics brought out by the Ministry of Agriculture also provide data relating to gross area sown or the total cropped area. Land is defined in the second approach as total cropped area and fallow lands. This approach is adopted by Subramonian (2004) and takes into consideration the increase in area sown more than once during the period. Thus, the study considers two alternative definitions of land input for the agriculture sector.
Definition 1: Land input= Net Cropped Area + fallow land
Definition 2: Land input= Gross Cropped Area + fallow land
The estimated trend growth rates of land input for the sub-periods and the entire study period is presented in Table 6A.1
Table 6A.1: Trend Growth Rates of Land Input |
(% per annum) |
Sector |
Period |
Land input, alternate estimates |
Gross cropped area + fallow land |
Net cropped area+ fallow land |
Agriculture, Hunting, Forestry & Fishing |
1980-1999 |
0.38 |
0.01 |
2000-2008 |
0.29 |
0.01 |
1980 -2008 |
0.35 |
0.01 |
| Source: Authors’ calculations. |
Next, to derive income shares, the share of intermediate inputs and labour input in gross output has been computed. To arrive at cost shares for land and capital input, the residual share is equally distributed between the two inputs. The income shares range from 0.38 to 0.40 for labour, 0.17 to 0.21 for both land and capital input, and 0.20 to 0.27 for intermediate inputs37.
Estimates of Productivity Growth for Agriculture Sector38
The gross output-based estimates of TFP for the agriculture sector have been computed using time series data for six inputs, namely, land, labour, capital, energy, material and services, for the period 1980 to 2008.
A comparison of TFP growth rates between the two sub-periods, viz., 1980 to 1999 and 2000 to 2008, is presented in Tables 6A.2 and 6A.3. It is observed that there was a significant fall in growth rates of Agriculture TFP in the latter period. For the entire period under study, growth of TFP accounts for more than half the output growth. The contribution of intermediate inputs to output growth is about one-sixth. The contributions of labour and capital input are about one-fifth and one-fourth, respectively, whereas the contribution of land input is quite modest at 2 per cent. The estimates of TFP in the agriculture sector, using the value added function framework, are reported in Table 6A.4, indicating deceleration in both gross value added growth in agriculture and TFP growth in the 2000s.
Table 6A.2: Trend Growth Rates of TFP of Agriculture Sector
(estimates based on Definition 1 of land) |
(% per annum) |
Sector |
Period |
TFPG, alternate estimates |
Growth in Gross output |
A1 |
B1 |
Agriculture, Hunting, Forestry & Fishing |
1980-1999 |
2.90 |
1.45 |
1.37 |
2000-2008 |
2.59 |
0.83 |
0.58 |
1980 -2008 |
2.82 |
1.29 |
1.17 |
Note: Land input= Net cropped area+ fallow land.
A1: TFPG computed using Labour input and capital stock.
B1: TFPG computed using Labour input and capital services.
Source: Authors’ calculations. |
Table 6A.3: Trend Growth Rates of TFP of Agriculture Sector
(estimates based on Definition 2 of land) |
(% per annum) |
Sector |
Period |
TFPG, alternate estimates |
Growth in Gross output |
A2 |
B2 |
Agriculture, Hunting, Forestry & Fishing |
1980-1999 |
2.90 |
1.38 |
1.30 |
2000-2008 |
2.59 |
0.77 |
0.52 |
1980 -2008 |
2.82 |
1.23 |
1.10 |
Note: Land input= Gross Cropped Area + fallow land.
A2: TFPG computed using Labour input and capital stock.
B2: TFPG computed using Labour input and capital services.
Source: Authors’ calculations. |
Table 6A.4: Trend Growth Rates of TFP of Agriculture Sector—Based on value added function framework
|
(% per annum) |
Sector |
Period |
TFPG, alternate estimates |
Real value added growth** |
A2 |
B2 |
Agriculture, Hunting, Forestry & Fishing |
1980-1999 |
3.10 |
1.89 |
1.78 |
2000-2008 |
2.61 |
1.30 |
0.71 |
1980 -2008 |
3.03 |
1.68 |
1.52* |
Note:* The trend growth rate in TFP in Agriculture using fixed weights as suggested by the Agriculture Cost and Prices Commission is found to be about 1.7 per cent per annum.
** Trend growth rates of real gross value added is based on aggregate production possibility frontier approach, which involves application of the Tornqvist index.
A2: TFPG computed using Labour input and capital stock.
B2: TFPG computed using Labour input and capital services.
Source: Authors’ calculations. |
Comparison with Productivity Studies in Agriculture
It would be useful here to compare our results obtained after including land input for agriculture with past productivity research. During the past 20 years or so, research on productivity growth in Indian agriculture has evolved (see reviews in Krishna, 2006; Kumar and Mittal, 2006; Kumar et al., 2008). Estimates of TFP growth are available for aggregate agriculture, crop sector, livestock sector and even individual crops, such as rice, wheat, maize and sugarcane. Table 6A.5 shows the estimates of TFP growth in the agriculture sector obtained in various studies.
Table 6A.5: Estimates of TFP Growth in Agriculture Sector |
Author (s) |
Period |
Estimated TFP growth rate
(% per annum) |
Sivasubramonian (2004) |
1950-1960
1960-1970
1970-1980
1980-1990
1990-1999 |
1.7
0.9
–0.4
1.9
1.7 |
Pratt, Yu and Fan (2008) |
1961-1973
1974-1980
1981-1991
1991-2006 |
–1.7
0.5
1.0
0.5 |
Fugli (2011) |
1981-1990
1991-2000
2001-2009 |
1.4
1.2
1.7 |
Bosworth, Collins and Virmani (2007) |
1980-2004
1983-1993
1993-1999
1999-2004 |
1.1
1.2
1.3
–0.1 |
Bosworth and Maertens (2010) |
1980-1990
1990-2000
2000-2006 |
1.9
0.7
0.9 |
Our Study |
1980-1999
2000-2008
1980-2008 |
1.8*
0.7*
1.5* |
| Note:*Estimates based on Gross value added framework. Refer to Table 6A.3 for estimates of TFP based on gross output framework. |
Although it is found that there are variations in the results of agriculture TFP studies for different periods, all support the following broad conclusions: TFP growth rates in agriculture were faster in the 1980s than in the 1970s. In the 1990s, TFP growth was slightly lower than in the decade of the 1980s and the growth rates further declined in the 2000s.Thus, the estimates presented in the table are roughly consistent with our results.
Chapter 7: Estimates of Productivity Growth for Broad Sectors and the Economy
7.1 Introduction
This chapter analyses trends in total factor productivity growth and labour productivity for the broad sectors and the whole economy. As noted earlier in the Report, the economy is divided into six broad sectors for the present analysis. These are (1) Agriculture, forestry and fishing, (2) Mining and quarrying, (3) Manufacturing, (4) Electricity, gas and water supply, (5) Construction and (6) Services.
The methodology for aggregation across industries is given in Section 7.2. Section 7.3 presents the inter-temporal variations in the pace of output growth (in terms of the growth in real GVA) in the economy and the six broad sectors during the period 1980-81 to 2008-09.This is followed by an analysis of trends in total factor productivity and labour productivity in Section 7.4. Section 7.5 presents an analysis of the sources of output growth of the Indian economy. Section 7.6 analyses the contributions of various industries to aggregate output and productivity growth. Section 7.7 provides the summary and conclusions of the chapter.
7.2 Methodology for Aggregation across Industries
In the analysis presented in the previous chapter, gross value of output (GVO) was taken as the measure of output of an industry and TFP growth was estimated using the gross output function framework in which capital, labour, materials, energy and services were taken as five inputs (in the case of agriculture, land was included among inputs). The Tornqvist index was applied to estimate TFP growth for each year during 1980-81 to 2008-09, which yielded an index of TFP for each industry for that period, permitting estimation of trend growth rate in TFP for the period under study (1980-81 to 2008-09) and two sub-periods (1980-81 to 1999-00 and 2000-01 to 2008-09).
The method of estimation of TFP growth for individual industries applied in Chapter 6 using a Gross Output framework cannot be readily applied to a higher level of aggregation. The main problem is that gross value of output cannot be added across industries to generate a measure of output at a higher level of aggregation, say for the economy or of any of the broad sectors. It becomes necessary, therefore, to consider appropriate methods of aggregation across industries consistent with the gross output function specification at the individual industry level. It is needless to say that one has to use the concept of value added to define an appropriate measure of output at the economy or broad sector level, but even here there are important issues of aggregation, i.e., how value added in different industries should be combined. A very useful discussion of the issues involved is found in Jorgenson et al. (2005).
There are three approaches to estimating TFP growth at an aggregate level. The first approach is the aggregate production function approach. This approach assumes the existence of an aggregate production function (say, at the level of the economy or at the level of manufacturing or services sector). Let the production function for a particular industry be defined as:
Y =f(X, K, L, T),
(7.1)
where Y denotes gross output, X intermediate inputs (in turn, a combination of materials, energy and services), K capital input, L labour input and T time (representing technology). Then, the concept of value added requires the existence of a value added function that, in turn, requires that the above production function be separable in K, L and T, i.e., the production function should take the following form:
Y =g(X, V(K, L, T)).
(7.2)
In this equation, V (.) is the value added function.
A number of highly restrictive assumptions have to be made for the aggregate production function approach. These include: (a) the value added function is the same across all industries up to a scalar multiple, (b) the functions that aggregate heterogeneous types of labour and capital must be identical in all industries, and (c) each specific type of capital and labour receives the same price in all industries. With these assumptions made, real value added at the aggregate level becomes a simple addition of real value added in individual industries. In notation,
where Vi is value added in the ith industry and V is the aggregate value added. Given aggregate value added and somewhat similarly defined aggregate capital and labour input, TFP growth at the aggregate level can be computed.
The second approach to aggregation is the aggregate production possibility frontier approach. It also needs the separability condition described in Equations 7.1 and 7.2 above, as in the case of the aggregate production function approach. The main difference between the aggregate production function approach and the aggregate production possibility frontier approach is that the latter relaxes the assumption that all industries must face the same value added function. Thus, the price of value added is no longer assumed to be the same across industries. The implication is that the aggregate value added from the aggregate production possibility frontier is given by the Tornqvist index of the industry value added as:
In this equation, wiis the share of industry i in aggregate value added in nominal terms. Thus, defining PV,i as the price of value added in industry i and Vi as the real value added in industry i, the share in question may be defined as:
And the two-period average is defined as:
Since each industry is subject to a production function separable into capital, labour and technology, as defined in Equation 7.2, real gross output, real value of intermediate inputs and real value added of industry i in a particular year t should satisfy the following relationship:
In this equation, uV and uX are the shares of value added and intermediate inputs in the gross value of output in nominal terms. Given data on growth in gross output and growth in intermediate input of a particular industry, the above equation yields the growth in real value added of that industry.
TFP growth from the aggregate production possibility frontier may be defined as follows:
In this equation K and L are aggregate capital input and labour input, respectively, and vK and vL are value shares (or income shares) of capital and labour, respectively. If one maintains the assumption that each specific type of capital and labour input has the same price in all industries, then each type of capital (labour) can be summed across industries and a Tornqvist index can be constructed to yield aggregate capital (labour) input. Alternatively, different types of capital input can be combined using a Tornqvist index into total capital input used in an industry and then industry-level growth in capital input can be combined with the help of a Tornqvist index to obtain growth in capital input at the aggregate level. In a similar manner, the growth in aggregate labour input can be computed.
The third approach to measuring the TFP index at a higher level of aggregation is to apply direct aggregation to industry-level estimates. This maintains the industry-level production accounts as the fundamental building block and begins with industry-level sources of growth. Of the three approaches described here, this is the least restrictive in terms of the assumptions involved. The following equation expresses the relationship between aggregate value added growth and the growth in capital and labour inputs and TFP in individual industries:
In this equation, vK is the value share of capital in gross output, vL is the value share of labour in gross output, vV is the share of value added in gross output, and wi is the share of industry i in aggregate value added in nominal terms. The bars indicate that the average of two periods, t and t-1, are to be taken. The last term in Equation 7.9 is:
This is the Domar aggregation of TFP growth rates at the individual industry level. Note that it is weighted average of industry-level TFP growth rates. But the weights add up to more than one.
For the analysis presented in Sections 7.3 and 7.4, the aggregate production possibility frontier approach has been taken, which, as mentioned above, is less restrictive than the aggregate production function approach. Real value added growth has been computed for each industry using Equation 7.7 and then these have been aggregated using Equation 7.439. The analysis of decomposition of output and labour productivity growth presented in Section 7.5 makes use of the third approach, i.e., the direct aggregation approach, since that approach simplifies decomposition.
7.3 Estimates of Output growth in the economy and the broad sectors
This section focuses on trend rates of growth of gross real value added measure of output. The trend growth rates over the entire period 1980-81 to 2008-09 and over the two sub-periods, 1980-81 to 1999-00 and 2000-01 to 2008-09, are analysed.
Before moving to the trend growth rates, a look at yearly growth rates at the economy level will be useful. Figure 7.1 depicts year-wise growth rates in real gross value added (GVA) in the Indian economy during 1980-81 to 2008-09.Two series on the growth rate in real GVA in the economy are presented. One of them, which is the preferred series, has been built from the estimated growth rates in real GVA at the disaggregated industry level. Tornqvist index of growth rate in real GVA has been computed for each year for each of the 26 study industries. Then, a weighted aggregation of the computed Tornqvist indices of growth in real GVA for the 26 industries has been taken to form the Tornqvist index of real GVA growth for the entire economy. This has been done for each year. This series is hereafter referred to as the aggregate production possibility frontier real GVA growth series (or PPF real GVA series for short). The second series involves simple aggregation of real GVA across industries. This is the real GDP series taken directly from NAS. This is hereafter referred to as simple aggregation-based real GVA series or aggregate production function value added series (or NAS real GVA series for short)40.
The two time series on the annual growth rates of real GVA at the economy level mentioned above are very similar; the peaks and troughs almost match and the direction of change in different years is mostly the same. The two series on real GVA growth rates have a correlation coefficient of 0.88.
 Based on the PPF real GVA growth series (the preferred series), the trend growth rate in real GVA of the Indian economy in the period 1980-81 to 2008-09 was 5.8 per cent per annum (Table 7.1).Trend growth rates in real GVA estimated for the sub-periods 1980-81 to 1999-00 and 2000-01 to 2008-09 were 5.2 and 7.6 per cent per year, respectively41, indicating that the growth rate in real GVA in the economy accelerated in the latter period by more than 2 percentage points per annum. The NAS real GVA series shows similar growth trends. In comparison with the real GVA series based on the Tornqvist index, the real GVA series based on simple aggregation (which is the NAS series) shows a slightly smaller hike in the trend growth rate in real GVA in the period 2000-01 to 2008-09. For the entire period 1980-81 to 2008-09, the trend growth rate in real GVA given by the NAS real GVA series is 5.8 per cent per annum, which matches that obtained from the PPF real GVA series.
Sector-wise, it appears that the acceleration in economic growth in India in the 2000s was essentially rooted in the growth acceleration experienced by manufacturing, construction and services. Among these sectors, the most marked growth acceleration occurred in construction.
| Table 7.1: Trend Growth Rate of Real Gross Value Added by Broad Sectors –Based on Tornqvist Index and Simple Aggregation, NAS Series |
(% per annum) |
Broad Sector |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
Series based on Tornqvist index |
Series based on simple aggregation |
Agriculture, Hunting, Forestry, Fishing |
3.10 |
2.61 |
3.03 |
3.08 |
2.61 |
2.96 |
Mining and Quarrying |
5.69 |
1.95 |
4.75 |
5.90 |
3.49 |
5.30 |
Manufacturing |
6.45 |
9.48 |
7.22 |
5.68 |
7.47 |
6.13 |
Electricity, Gas and Water Supply |
6.59 |
9.99 |
7.44 |
7.59 |
4.70 |
6.86 |
Construction |
1.51 |
9.36 |
3.48 |
4.70 |
9.99 |
6.03 |
Services |
6.49 |
8.94 |
7.11 |
6.62 |
9.07 |
7.23 |
Total Economy |
5.24 |
7.55 |
5.82 |
5.26 |
7.34 |
5.78 |
| Source: Authors’ calculations. |
It would be useful to consider here some alternative indicators on the growth of production in certain sectors of the economy and make a comparison with the growth rates in real GVA obtained in this study. Trend growth rates based on the Index number of Industrial Production (IIP) for mining, manufacturing and electricity are shown in Table 7.2 for the sub-periods 1980-81 to 1999-00 and 2000-01 to 2008-09, and a comparison is made with the trend growth rate in real GVA in mining & quarrying, manufacturing, and electricity, gas & water supply sectors. Similarly, trend growth rates in the index of agricultural production are compared with the trend growth rates in real GVA of the Agriculture, forestry & fishing sector.
For the agriculture, mining and manufacturing sectors, it is comforting to note that the growth rates in the production index are similar to the estimated growth rates in real GVA, and that the inter-temporal changes in the rates of growth match across the three sets of growth rates. The growth rate has been relatively low in the agriculture sector with deceleration in the rate of growth in the 2000s. In manufacturing, there has been an acceleration in the rate of growth in the 2000s, while in the mining sector output/production growth decelerated in the 2000s even as the economy as a whole experienced a step-up in the rate of growth.
For the electricity sector, the IIP series and the real value added series reported in NAS indicate that the growth of output of this sector decelerated in the 2000s, despite a pick-up in the rate of economic growth in India during this period. The PPF real GVA series that is based on the Tornqvist index, however, indicates that the rate of growth in real value added accelerated in the 2000s. Thus, there is disagreement among the three series in regard to inter-temporal changes in the growth rate of output of the electricity sector.
Table 7.2: Comparison of Estimated Trend Growth Rates in Output from Alternative Data |
Sector |
Production index |
Real Gross Value Added – PPF Series |
Real Gross Value Added – NAS series |
1980 to 1999 |
2000 to 2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 1999 |
2000 to 2008 |
Agriculture |
2.7 |
1.5 |
3.10 |
2.61 |
3.08 |
2.61 |
Mining |
4.9 |
2.5 |
5.69 |
1.95 |
5.90 |
3.49 |
Manufacturing |
6.5 |
8.3 |
5.94 |
6.04 |
5.68 |
7.47 |
Electricity |
7.6 |
3.9 |
6.59 |
9.99 |
7.59 |
4.70 |
Source: Authors’ calculations.
Note: Production Index was taken from Central Statistics Office, Government of India and Handbook of Statistics of the Indian Economy published by the Reserve Bank of India. |
From the analysis above, three interesting points emerge: (a) a significant increase in the growth rate of the construction sector in the 2000s compared to the two previous decades, (b) a marked fall in the growth rate of the mining sector in the 2000s despite a step-up in the growth rate of the economy, and (c) a modest acceleration in the growth of real value added in the electricity sector in the 2000s indicated by the preferred real GVA series even though the production of electricity in physical units has decelerated in the 2000s. How can these three points be explained?
The significant increase in the growth rate of output of the construction sector in the 2000s is consistent with the fact that the rate of investment in India went up considerably in this decade. Between 2000-01 and 2008-09, the rate of investment in India increased from 24.4 per cent to 34.3 per cent, i.e., more than one percentage point increase per year. By contrast, in the period 1980-81 to 2000-01, the increase in the rate of investment was relatively much smaller; the increase was from 19.2 per cent to 24.4 per cent, i.e., a quarter percentage point hike per year. The hike in the rate of investment in the 2000s was coupled with relatively fast growth in GDP. The series on real investment in construction reported in NAS show a growth rate of about 10 per cent per annum in the period 2000-01 to 2008-09 as against a growth rate of about 5 per cent per annum in the period 1980-81 to 2000-01. This is in agreement with the growth rates in real GVA in the construction sector shown in Table 7.1
Turning to the mining sector, coal, iron ore and crude oil form a major part of the value of output of the Indian mining industry. Production of coal increased from 119 million tonnes in 1980-81 to 333 million tonnes in 2000-01 and further to 525 million tonnes in 2008-09. The growth rate in coal production was 5.3 per cent per annum between 1980-81 and 2000-01, while the growth rate between 2000-01 and 2008-09 was 5.9 per cent per annum. Thus, there was acceleration in the growth rate of coal output in India in the 2000s. The same pattern is observed for iron ore. The production of iron ore increased from 42 million tonnes in 1980-81 to 81 million tonnes in 2000-01 and further to 213 million tonnes in 2008-09. The growth rates were 3.3 per cent per annum between 1980-81 and 2000-01 and 12.8 per cent per annum between 2000-01 and 2008-09. Therefore, the deceleration in the growth rate of output/production in the mining sector in the 2000s appears to be traceable mostly to the rate of growth in crude oil production. Between 1980-81 and 2000-01, on-shore crude oil production increased from 5.5 million tonnes to 11.8 million tonnes (growth rate, 3.9 per cent per annum).Between 2000-01 and 2008-09, there was a fall in on-shore crude oil production in India, from 11.8 to 11.3 million tonnes. Taking on-shore and off-shore crude oil production together, the total production of crude oil increased from 10.5 million tonnes in 1980-81 to 32.4 million tonnes in 2000-01.Subsequently, there was a very small increase in domestic crude oil production. In 2008-09, the total crude oil production (on-shore plus off-shore) was 33.5 million tonnes. In 2008-09, crude oil formed about one-third of the total value of mineral production. The virtual stagnation in the domestic production of crude oil in the 2000s must have been the main cause, or an important cause, of the deceleration in the rate of output growth in the mining sector in the period 2000-01 to 2008-09. It may be mentioned in this context that the crude oil reserves of the country increased sharply from about 450 billion tonnes in 1980 to about 800 billion tonnes in 1990. Since then, there has been little increase. The crude oil reserve in 2008 was a little less than 800 billion tonnes.
It is evident that while domestic production of crude oil has stagnated, there has been a significant increase in imports of crude oil. Between 2000-01 and 2008-09, imports of crude oil increased from 74.1 million tonnes to 132.8 million tonnes. Evidently, there has been a huge increase in the demand for crude oil in the country; but due to certain supply-side constraints an increasing portion of the demand has been met by imports. The sluggish growth in crude oil production in the country explains to a large extent the observed deceleration in output growth in the mining sector.
As regards the electricity sector, in terms of physical production volume, it experienced a deceleration in growth in the 2000s. Gross generation of electricity increased from 119.3 billion KWH in 1980-81 to 560.8 billion KWH in 2000-01 and then to 840.9 billion KWH in 2008-09.The annual rate of growth was 8 per cent during 1980-81 to 2000-01 and lower at 5.2 per cent during 2000-01 to 2008-09.
Since the rate of growth of the Indian economy accelerated in the 2000s, the slowdown in the growth rate of electricity generation may appear somewhat surprising. An analysis of data on electricity generation capacity reveals that there has also been a slight reduction in the growth rate of generation capacity. Between 1980-81 and 2000-01, the growth rate of power generation capacity was 6.5 per cent per year, which came down to 5 per cent per year in the period 2000-01 to 2008-09. This slowdown in the growth rate of capacity may have adversely affected the growth in electricity generation. Also, there are probably some supply-side problems, for instance, shortages of coal42, which might have hampered the growth of the electricity sector.
Another phenomenon to which attention needs to be drawn is the growth in captive power generation. Capacity for captive power generation was around 3,000MW in 1980-81. By 2007-08, it had increased to more than 20,000MW (Nag, 2010).It is, however, not clear if one can attribute the observed deceleration in the growth of electricity generation in the country to increases in captive power generation, because going by the available estimates even the growth in captive power generation has decelerated in the 2000s.
A detailed study is needed to ascertain the reasons for the slowdown in the electricity sector in the 2000s. Perhaps, there were serious supply-side problems because of which the sector could not grow as fast as it did in the previous two decades. But there may be some demand-side factors as well. One factor that could provide a partial explanation for the deceleration in the growth of the electricity sector is the significant improvement in energy efficiency made by Indian manufacturing in the period since 1992. Between 1992-93 and 2008-09, the energy intensity of India’s organised manufacturing (measured by the ratio of energy cost to the value of output, both deflated) fell by about 60 per cent (Goldar, 2011). The physical measure of energy intensity in organised manufacturing in TJ per ` billion of real output fell by 48 per cent between 1992 and 2005.
It is evident from the above that the physical production of the electricity sector has decelerated in the 2000s. This is reflected in the real value added series given in NAS, probably because the NAS value added series for the electricity sector makes use of the estimates of physical production of the electricity sector for the purpose of estimation of value added. But the real value added series for the electricity sector constructed for this study using the Tornqvist index and aggregate production possibility frontier approach shows a modest acceleration in the 2000s. This probably shows that value added per KWH of electricity production has been increasing in the 2000s.
One factor that has caused value added in the electricity sector to grow faster than the physical production is that there has been an improvement in the efficiency with which intermediate inputs are used. Available data reveals that the electricity sector increasingly economised on the use of energy input and services input in the 2000s, which explains the rise in value added per KWH of production in the electricity sector.
7.4 Estimates of Productivity Growth in the Economy and Broad sectors
Estimated trend rates of growth in labour productivity (measured by the ratio of real gross value added to the number of persons employed) and total factor productivity (based on the aggregate production possibility frontier approach and Tornqvist index of value added at the individual industry level) and aggregate production function value added approach during 1980-81 to 2008-09 are presented in Tables 7.3 and 7.4. Three alternate estimates of TFP growth are shown in the table. One set is based on number of persons employed and capital stock, a second set is based on labour input (combining persons employed and change in labour composition) and capital stock, and a third set is based on labour input and capital services (incorporating changes in the asset composition of capital stock)43.
Table 7.3: Trend Growth Rate of Labour Productivity and Total Factor Productivity by Broad Sector, 1980 to 2008 |
Aggregate production possibility frontier value added |
Broad Sector |
Real Value Added
per Person |
Total factor productivity, alternative estimates |
A2 |
B2 |
C2 |
Agriculture, Hunting, Forestry, Fishing |
2.10 |
1.81 |
1.68 |
1.52 |
Mining and Quarrying |
3.22 |
0.23 |
–0.17 |
–0.24 |
Manufacturing |
5.43 |
1.74 |
1.30 |
0.73 |
Electricity, Gas and Water Supply |
6.05 |
2.94 |
2.62 |
2.60 |
Construction |
–2.48 |
–2.95 |
–3.31 |
–3.31 |
Services |
3.56 |
2.59 |
2.07 |
1.84 |
Total Economy |
4.04 |
2.42 |
1.74 |
1.40 |
Note: Alternative A2: TFPG computed using labour person and capital stock.
Alternative B2: TFPG Computed using labour input and capital stock.
Alternative C2: TFPG computed using labour input and capital services.
Source: Authors’ calculations. |
Table 7.4: Trend Growth Rate of Labour Productivity and Total Factor Productivity by Broad Sector, 1980 to 2008 |
Aggregate production function value added |
Broad Sector |
Real Value Added per Person |
Total Factor Productivity, alternative estimates |
A1 |
B1 |
C1 |
Agriculture, Hunting, Forestry, Fishing |
2.08 |
1.79 |
1.66 |
1.50 |
Mining and Quarrying |
3.76 |
0.77 |
0.38 |
0.30 |
Manufacturing |
4.34 |
0.65 |
0.21 |
–0.36 |
Electricity, Gas and Water Supply |
5.46 |
2.36 |
2.04 |
2.01 |
Construction |
0.07 |
–0.40 |
–0.76 |
–0.76 |
Services |
3.73 |
2.71 |
2.19 |
1.96 |
Total Economy |
3.86 |
2.38 |
1.69 |
1.36 |
Note: Alternative A1: TFPG computed using labour person and capital stock.
Alternative B1: TFPG Computed using labour input and capital stock.
Alternative C1: TFPG computed using labour input and capital service.
Source: Authors’ calculations.
|
The estimated rates of total factor productivity (TFP) growth in the economy and the broad sectors presented in Table 7.3 are higher than the estimates presented in Table 7.4 in some cases and lower in other cases. Methodologically, the estimates based on the aggregate production possibility frontier approach are to be preferred44. On methodological considerations, the C2 measure of TFP growth is the most preferred among the six measures presented in these tables.
Going by the estimates shown under column C2, the trend rate of TFP growth in the Indian economy in the period 1980-81 to 2008-09 was about 1.4 per cent per annum. Services contributed a dominant portion of the TFP growth achieved at the economy level.
The rate of TFP growth in the construction sector during 1980-81 to 2008-09 was negative. One reason for the observed relatively poor productivity growth performance of this sector is that there has been a rapid increase in employment in construction. The growth rate of employment in construction was about 6.0 per cent per annum as compared with growth of 1.8 per cent per annum in the aggregate employment in the economy. Further, in the construction sector, the growth of all inputs has been relatively faster than the growth rate in gross output.
Turning to labour productivity growth, the trend rate of growth in labour productivity in the economy during 1980-81 to 2008-09 was about 4 per cent per annum. Labour productivity growth was relatively higher in the manufacturing and electricity sectors. The worst performers were the agriculture and construction sectors, with the latter showing virtually no increase in labour productivity or a fall in labour productivity.
Comparison of TFP Growth between Sub-periods
A comparison of TFP growth rates between the periods 1980-81 to 1999-00 and 2000-01 to 2008-09 is presented in Table 7.5.
Table 7.5: Period-wise Trend Growth Rate of Total Factor Productivity by Broad Sectors |
(% per annum) |
Broad Sector |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
1980 to 1999 |
2000 to 2008 |
1980 to 2008 |
Using Labour persons and capital stock (based on A2 estimates) |
Using Labour input and capital stock (based on B2 estimates) |
Using Labour input and capital service (based on C2 estimates) |
Agriculture, Forestry, Fishing |
1.99 |
1.26 |
1.81 |
1.89 |
1.3 |
1.68 |
1.78 |
0.71 |
1.52 |
Mining & Quarrying |
0.65 |
–1.03 |
0.23 |
0.42 |
–1.91 |
–0.17 |
0.22 |
–1.59 |
–0.24 |
Manufacturing |
1.27 |
3.13 |
1.74 |
0.81 |
2.75 |
1.3 |
0.04 |
2.76 |
0.73 |
Electricity, Gas & Water Supply |
1.51 |
7.2 |
2.94 |
1.22 |
6.8 |
2.62 |
1.14 |
6.93 |
2.96 |
Construction |
–3.82 |
–0.34 |
–2.95 |
–4.18 |
–0.7 |
–3.31 |
–4.19 |
–0.69 |
–3.31 |
Services |
2.5 |
2.83 |
2.59 |
1.98 |
2.31 |
2.07 |
1.74 |
2.14 |
1.84 |
Total Economy |
2.23 |
2.99 |
2.42 |
1.52 |
2.38 |
1.74 |
1.11 |
2.26 |
1.4 |
Source: Authors’ calculations. |
At the aggregate economy level, there was a significant increase in the growth rate of TFP in the latter period. Going by the C2 estimates, the trend rate of TFP growth in the economy increased from about 1.1 per cent per annum during 1980-81 to 1999-00 to about 2.3 per cent per annum during 2000-01 to 2008-09.A similar step-up in the rate of TFP growth was noticed in the manufacturing and electricity sectors. The hike in the rate of TFP growth was much larger in the case of the electricity sector. In the services sector too, there was an increase in the growth rate of TFP, but the magnitude of the increase was small. In all three sets of estimates, the hike in the rate of TFP growth in the latter period is about 0.3 to 0.4 percentage points per annum.
Among the six broad sectors, the largest increase in the rate of TFP growth between the two sub-periods took place in the electricity sector. The hike was more than 5 percentage points per annum. There is a clear indication that the electricity sector increasingly economised on the use of energy input and services input in the 2000s. This raised value added per KWH of production and, thus, had a favourable effect on TFP. The increase in the plant load factor and the reduction in T&D losses have obviously contributed to TFP growth in the electricity sector.
7.5 Sources of GVA Growth
The decomposition of GVA growth during 1980-81 to 2008-09 into its sources, viz., factor inputs and TFP growth, is shown in Table 7.6 for different broad sectors and the economy.
For the economy as a whole, the contribution of TFP growth to GVA growth was about one-fourth, while about one-half of the GVA growth was contributed by growth in capital input(along with the contribution of land input).
The individual sectors differ greatly with regard to the sources of growth.TFP growth contributes significantly to output growth in the agriculture, electricity and services sectors, but not in the other three sectors. The relative contribution of TFP growth to GVA growth is the highest for the agriculture sector, followed by the electricity sector.
Table 7.6: Trend Growth Rate in Real Value Added and Contribution of Factor Inputs and TFP to GVA growth by Broad Sectors, 1980 to 2008 |
(% per annum) |
Broad Sector |
Real value added growth |
Contribution of Labour persons |
Contribution of Labour quality |
Contribution of Capital services |
TFP growth |
Agriculture |
3.03 |
0.37 |
0.15 |
0.99* |
1.52 |
Mining & Quarrying |
4.75 |
0.68 |
0.38 |
3.93 |
–0.24 |
Manufacturing |
7.22 |
0.68 |
0.44 |
5.37 |
0.73 |
Electricity, Gas & Water Supply |
7.44 |
0.66 |
0.34 |
3.49 |
2.96 |
Construction |
3.48 |
5.21 |
0.21 |
1.37 |
–3.31 |
Services |
7.11 |
1.73 |
0.53 |
3.00 |
1.84 |
Total Economy |
5.82 |
0.84 |
0.69 |
2.89* |
1.40 |
Note: * Includes the contribution of land.
Source: Authors’ calculations. |
During the period under consideration, GVA growth in mining and construction was primarily on account of inputs. Growth in capital input accounted for about 80 per cent of output growth in mining. In construction, by contrast, output growth was mainly driven by growth in labour persons employed. TFP growth accounted for about one-fourth of the real GVA growth achieved by the services sector. Besides productivity growth, growth in labour and capital input also contributed to services sector growth.
Next, the analysis of sources of GVA growth is undertaken by sub-periods, 1980-91 to 1999-00, and 2000-01 to 2008-09 (Table 7.7). For the whole economy, the growth rate in real GVA increased by about 2.3 percentage points in the latter period, which can be traced to faster growth in capital input and in TFP, a little more than one percentage point each.
Table 7.7: Trend Growth Rate in Real Value Added and Contribution of Factor Inputs and TFP to GVA growth, by sub-period |
(% per annum) |
Broad Sector |
Period |
Real value added growth |
Contribution of Labour persons |
Contribution of Labour quality |
Contribution of Capital services |
TFP growth |
Agriculture, Hunting, Forestry, Fishing |
1980-99 |
3.1 |
0.54 |
0.11 |
0.67 |
1.78 |
2000-08 |
2.61 |
–0.02 |
0.24 |
1.68 |
0.71 |
Mining & Quarrying |
1980-99 |
5.69 |
0.70 |
0.14 |
4.63 |
0.22 |
2000-08 |
1.95 |
0.54 |
0.57 |
2.43 |
–1.59 |
Manufacturing |
1980-99 |
6.45 |
0.67 |
0.46 |
5.28 |
0.04 |
2000-08 |
9.48 |
0.68 |
0.42 |
5.62 |
2.76 |
Electricity, Gas & Water Supply |
1980-99 |
6.59 |
0.79 |
0.37 |
4.29 |
1.14 |
2000-08 |
9.99 |
0.46 |
0.28 |
2.31 |
6.93 |
Construction |
1980-99 |
1.51 |
4.51 |
0.18 |
1.01 |
–4.19 |
2000-08 |
9.36 |
7.32 |
0.31 |
2.43 |
–0.69 |
Services |
1980-99 |
6.49 |
1.92 |
0.51 |
2.32 |
1.74 |
2000-08 |
8.94 |
1.43 |
0.60 |
4.78 |
2.14 |
Total Economy |
1980-99 |
5.24 |
0.91 |
0.71 |
2.51 |
1.11 |
2000-08 |
7.55 |
0.72 |
0.69 |
3.89 |
2.26 |
| Source: Authors’ calculations. |
7.6 Contributions of Various Industries to Aggregate Output and Productivity Growth
The contributions of different industries to aggregate output (real gross value added) growth during 1980-81 to 2008-09 are shown in Table 7.8. The largest contributors to real GVA growth at the aggregate level included trade, agriculture, hunting, forestry & fishing, ‘other services’, financial services, public administration & defence, transport & storage and basic metals & fabricated metal products. The services sector has made a major contribution to overall GVA growth, while the contribution of manufacturing has been modest.
Table 7.8: Industry Contributions to Aggregate Real GVA Growth, 1980-2008 |
Industry No. |
Industry description |
Share in GVA,
1980-2008 |
Trend Growth rate in real GVA,
1980-2008,
% per annum |
Contribution to Aggregate Real GVA Growth,
% per annum |
1 |
Agriculture, Hunting, Forestry & Fishing |
0.27 |
3.00 |
0.80 |
2 |
Mining & Quarrying |
0.03 |
4.78 |
0.12 |
3 |
Food products, Beverages & Tobacco |
0.02 |
7.00 |
0.15 |
4 |
Textiles, Textile products, Leather & Footwear |
0.03 |
7.57 |
0.20 |
5 |
Wood & products of Wood |
0.01 |
–3.02 |
–0.01 |
6 |
Pulp, Paper, Paper products, Printing & Publishing |
0.01 |
6.27 |
0.03 |
7 |
Coke, Refined Petroleum products & Nuclear Fuel |
0.01 |
0.60 |
0.00 |
8 |
Chemicals & Chemical products |
0.02 |
10.17 |
0.21 |
9 |
Rubber & Plastic products |
0.01 |
8.27 |
0.05 |
10 |
Other Non-Metallic Mineral products |
0.01 |
7.73 |
0.07 |
11 |
Basic Metals & Fabricated Metal products |
0.02 |
10.74 |
0.25 |
12 |
Machinery, nec |
0.01 |
4.56 |
0.05 |
13 |
Electrical & Optical equipment |
0.01 |
12.55 |
0.16 |
14 |
Transport equipment |
0.01 |
10.63 |
0.09 |
15 |
Manufacturing, nec; recycling |
0.01 |
10.32 |
0.09 |
16 |
Electricity, Gas & Water Supply |
0.02 |
8.16 |
0.18 |
17 |
Construction |
0.06 |
2.83 |
0.16 |
18 |
Trade |
0.13 |
7.04 |
0.90 |
19 |
Hotels & Restaurants |
0.01 |
6.63 |
0.07 |
20 |
Transport & Storage |
0.06 |
5.23 |
0.29 |
21 |
Post & Telecommunications |
0.01 |
14.90 |
0.19 |
22 |
Financial Services |
0.05 |
10.36 |
0.49 |
23 |
Public Administration & Defence; Compulsory Social Security |
0.06 |
5.88 |
0.35 |
24 |
Education |
0.03 |
6.95 |
0.22 |
25 |
Health & Social Work |
0.01 |
6.26 |
0.08 |
26 |
Other Services |
0.11 |
6.49 |
0.70 |
|
Total |
1.00 |
|
5.88 |
| Source: Authors’ calculations. |
7.7 Summary
This chapter analysed trends in output growth, total factor productivity growth and labour productivity growth during 1980-2008 for the Indian economy and the six broad sectors. The analysis is based on a value added function framework, which became necessary because gross value of output cannot be added across industries to form an appropriate measure of output at an aggregate level. Of the three approaches to aggregation available, the analysis presented in the chapter relied mainly on the aggregate production possibility frontier approach, though for some part of the analysis a relatively less restrictive approach, namely, direct aggregation of industry-level estimates, was also employed.
Analysis of real value added growth revealed that at the economy level, the trend growth rate in real GVA increased by about 2 percentage points between 1980-99 and 2000-08, a hike from 5.2 per cent per annum during 1980-99 to 7.6 per cent per annum during 2000-08.The growth acceleration was rooted in manufacturing, construction and services.By contrast, the mining sector experienced a marked fall in output growth rate in the 2000s, which is traceable to incremental domestic demand for crude oil being met from imports rather than domestic production.
The estimates of TFP growth based on labour input and capital services (also land input in the case of agriculture and the whole economy) presented in the chapter indicate that the trend rate of growth in TFP in the economy was about 1.4 per cent per annum during 1980-2008. Sector-wise, the trend rates of growth in TFP per year during 1980-2008 were 2.6 per cent in the electricity sector, 1.8 per cent in the services sector, 1.5 per cent in the agriculture sector and 0.7 per cent in the manufacturing sector. There was a marked fall in TFP in the construction sector at the rate of 3.3 per cent per annum during 1980-2008. In the mining sector too, the trend in TFP growth was downward; the trend growth rate during 1980-2008 was –0.24 per cent per annum.
For the economy, the trend rate of growth in labour productivity during 1980-2008 was about 4per cent per annum. Labour productivity growth was relatively higher in the manufacturing and electricity sectors, at 5.4 and 6.0 per cent per annum, respectively. In the mining and services sectors, the trend growth rate in labour productivity was only a shade lower than that of the whole economy. The worst performers are the agriculture and construction sectors. For the construction sector, there are indications of virtually no increase in labour productivity or a fall in labour productivity.
At the aggregate economy level, there was an appreciable increase in the growth rate of TFP in the 2000s. The rate of growth in TFP increased from about 1.1 per cent per annum during 1980-99 to 2.3 per cent per annum during 2000-08. The manufacturing sector and the electricity sector experienced a marked increase in the rate of TFP growth in the 2000s. In the case of electricity, the hike was from 1.1 per cent per annum during 1980-99 to 6.9 per cent per annum during 2000-08. In the case of manufacturing, the increase was from 0.04 per cent per annum during 1980-99 to 2.76 per cent per annum during 2000-08. An improvement in the rate of TFP growth was also experienced by the services sector. On the other hand, the rate of TFP growth came down in the 2000s in the agriculture and mining sectors.
An analysis of industry contributions to aggregate TFP growth revealed that the most important contributors to aggregate TFP growth included agriculture, trade, public administration & defence, hunting, forestry & fishing, ‘other services’, post & telecommunications, electrical & optical equipment, electricity, gas & water supply, basic metals & fabricated metal products and financial services.
A similar analysis was undertaken of the contributions of different industries to the observed hike in the rate of TFP growth in the 2000s at the aggregate economy level. This analysis revealed that the top four largest contributors to the increase in TFP growth rate in the economy were basic metals & fabricated metal products, financial services, post &telecommunications and transport & storage. Construction, electricity, gas & water supply, public administration &defence, electrical & optical equipment and chemicals & chemical products have also contributed significantly to the hike in the rate of TFP growth in the economy in the 2000s compared to the period 1980-99. On the other hand, coke & refined petroleum products, ‘other services’ and agriculture, hunting, forestry & fishing have contributed negatively to the change in TFP growth in the economy, i.e., there was a fall in the rate of TFP in these industries, which pulled down the overall TFP growth in the economy.
Chapter 8: Summary and Conclusions
This final chapter outlines the main findings of the report, draws possible implications and suggests new directions for research. Our main focus in this research project was to generate datasets, allowing estimation of productivity growth at the industry level as well as for the economy and its broad sectors. This report has documented and analysed India’s productivity performance for the period 1980-2008 using both value added as well as gross output specification of the production function. The value added framework incorporated two inputs—labour and capital—whereas using a gross output specification of the production function enabled us to consider the explicit role of intermediate inputs—energy, materials and services. Studies that focus on the value added measure of output assume that intermediate inputs are used in fixed ratios with gross output regardless of their prices. In gross output specification, intermediate inputs are treated symmetrically with factor inputs, namely, labour and capital, so that substitution and complementarities among inputs are reflected in their use as prices vary.
The construction of the time series of the inputs—labour, capital and intermediate inputs of energy, materials and services at the industry level—comprised a significant step in the computation of productivity growth for the individual industries that comprise the economy.
For all 26 industries, the median growth rate of gross output was 6.9 per cent per annum. Output growth is found to be most rapid in post & telecommunications (14.16 per cent). Of the five fastest growing industries, two are producers of services (post & telecommunications and financial services) and three are in the manufacturing sector (electrical & optical equipment, manufacturing nec, and rubber & plastic products). All these industries posted growth rates in excess of 9.4 per cent during the period 1980 to 2008. As regards value added growth, during the period 1980-2008 the trend growth in gross value added for services has been reasonably high and consistent, at 7.23 per cent per annum. The growth performance of the manufacturing sector stood at 6.13 per cent per annum during the period under study. However, the growth record of agriculture reveals one of the major weaknesses of the Indian economy; the trend growth rate in GVA for agriculture was 2.96 per cent per annum over the study period. Broad sectors such as manufacturing, construction and services experienced acceleration in value added growth rate between 2000 and 2008. Among these three sectors, the most marked growth acceleration occurred in construction. The trend growth rate in real gross value added of construction increased from 4.7 per cent per annum during 1980-81 to 1999-00 to close to 10 per cent per annum from 2000-01 to 2008-09.
The growth rate of labour input (Index of persons employed multiplied by index of labour composition) shows that labour input grew the fastest in post & telecommunications, machinery, nec, construction, rubber & plastic products, other services and financial services. Over the period 1980-2008, the growth in persons employed was driven mainly by construction and the services sectors and the agriculture sector was a laggard.
The growth rate of capital services in the economy was 6.46 per cent per year. It was the highest at 8.76 per cent in the broad sector of manufacturing and the lowest at 3.51 per cent in the agriculture sector. The growth rate in the services sector was also quite high at 5.89 per cent. The inter-industry differences in growth rates were very large: 3.51 per cent in agriculture to 12.06 per cent in transport equipment.
As regards the trend rates of growth for intermediate inputs, enormous heterogeneity is observed across industries in the range of 12.77 per cent (for post & telecommunications) to 2.31 per cent (for agriculture). The growth in intermediate inputs was the fastest for post & telecommunications, electrical & optical equipment, financial services, rubber & plastic products, manufacturing nec. and transport & storage. Comparing output growth with input growth, three of the fastest growing industries in input growth were also the fastest in output growth. The trend growth rate of material input for the economy stood at 6.81 per cent and that of energy and services at 7.08 and 6.95 per cent, respectively. At the industry level, wide variations in usage of intermediate inputs is observed.
While the findings of this study confirm the view of the dominant role of input accumulation as against productivity growth in explaining India’s economic growth, it is also able to capture, through the creation of new datasets for measures of labour as well as capital input, the contributions of inputs in terms of both quantity as well as quality to productivity growth. Estimates of productivity growth—both labour productivity (LP) as well as total factor productivity (TFP) growth—at the disaggregated 26-industry level show wide inter-industry variations as well as change over time. The main finding is that since 2000 there has beena revival of productivity growth in many industries comprising the Indian economy. Comparing the two sub-periods 1980-1999 and 2000-2008, the majority of the disaggregated industries are found to show faster TFP growth in the second period. At the sectoral level, however, there was a decline in productivity performance in three broad sectors—agriculture, construction and mining & quarrying— while the remaining three sectors—manufacturing, electricity, gas & water, and services—show improvements in productivity. This shows that since 2000, TFP has not been a narrow phenomenon but is broad-based across many industries. Similar results hold for labour productivity growth. It indicates that nearly two decades of policy reforms in the areas of trade and industry have made a difference.
One important and significant observation from this report is that the intermediate inputs—materials, energy and services—are important in understanding the production process across Indian industries. Intermediate material input turns out to be the dominant input in most industries, the exceptions being a few industries, such as agriculture, mining & quarrying, wood, post & telecommunications, financial services, education and health & social work, where the capital input contribution was higher than that of intermediate inputs.
An attempt is also made to distinguish heterogeneous inputs, especially with regard to capital and labour inputs, in order to understand industry-level growth dynamics. To accomplish this, the traditional breakdown of capital and labour into quantity and quality components has been examined. The report observes higher contribution to output growth across most industries from capital services as against capital stock. In terms of labour input, however, it is found that the labour person measure makes a higher contribution than quality (education) as regards output growth for the 24 industries.
The report also provides productivity growth estimates for broad sectors of the Indian economy. Services, electricity and agriculture are the three broad sectors that have recorded a relatively higher rate of productivity performance for the period 1980-2008. The rate of productivity growth in services and the relatively higher share of services in aggregate output of the Indian economy confirm that services has made a large contribution to the observed aggregate economy productivity growth. Finally, the results for broad sectors confirm that for the economy as a whole the contribution of productivity growth to output growth is minimal and, as with the industry-level findings, inputs account for a dominant share of output growth.
The findings will prove useful for policy analysis, since the research outcomes, particularly both total factor and labour productivity growth, could provide further motivation for exploring the links between policy changes and improvements in industrial productivity to enhance the competitiveness of the economy. The drive in India after the 1980s and during the 2000s towards making the economy more open in terms of lowering the regulatory restrictions in the product and service markets may hold the potential to increase productivity across industries in the coming decades. The availability of datasets on industrial performance in terms of the productivity yardstick could help in the analysis of what influences productivity enhancement at the level of industries for the economy.
Acknowledgements by the Research Team
The Report titled ‘Estimates of Productivity Growth for Indian Economy’ relates to the research carried out in Phases I and II of the three-phase India KLEMS research project being undertaken at ICRIER in collaboration with the Reserve Bank of India.
The research work was carried out under the guidance of Professor B. N. Goldar by a team comprising Dr. Deb Kusum Das, Professor Suresh Aggarwal, Dr. Abdul Azeez Erumban, Ms Sreerupa Sengupta, Ms Kuhelika De and Shri Pilu Chandra Das. Other members in the team in the earlier stages were Ms Deepika Wadhwa, Shri Gunajit Kalita, Shri Suvojit Bhattacharjya, Shri Jaggannath Mallick and Shri Parth Goyal. The project has been co-ordinated by Dr. Deb Kusum Das. The construction of the intermediate input series was supervised by Shri M. R. Saluja. We thank Groningen Growth and Development Centre, University of Groningen, Netherlands for technical support as well as for intellectual support in the form of research time from Dr. Abdul Azeez Erumban.
The team benefitted greatly from a wide range of consultations during several workshops held at ICRIER. We thank Shri G. Raveendran (CSO), Professor T. S. Papola (ISID), Shri Bimal Giri (CSO), Dr. T.C.A. Anant (CSO) and Professor K. Sundaram (DSE) for providing detailed comments on the methodology followed for construction of labour input by quantity as well as quality. The methodology for construction of capital input and capital services was commented on by Professor Ravindra Dholakia (IIMA), Professor Pushpa Trivedi (IITB) and Shri Nilachal Ray (CSO) and we express our sincere thanks. We would like to thank Dr. A. C. Kulshrestha (formerly, CSO) and Dr. Kaustuva Barik (IGNOU) for providing detailed comments on the methodology followed for construction of intermediate inputs.
Two annual work-in-progress seminars were held during the first two phases of the India KLEMS research project. For the first workshop held in January 2011, we would like to thank Dr. Pronob Sen (CSO) (Session I: Productivity Measurement in KLEMS framework), Professor T. S. Papola (ISID) (Session II A: Measuring Labour Input), Professor S. R. Hashim (ISID) (Session II B: Measuring Capital Input) and Dr. Subashish Gangopadhyay (IDF) (Session III: Estimates of Productivity for Indian Economy) for chairing the sessions and providing valuable inputs on methodological issues. To Professor K Sundaram (Ex-DSE), Professor Madhusudan Dutta (GID) and Dr. Simrit Kaur (University of Delhi) our thanks for comments provided as discussants. The second workshop was held in April 2012 and we thank Dr. T. C. A. Anant (CSO) (Session I: Construction of Gross Output and Intermediate input Series) and Professor Aditya Bhattacharjea (DSE) (Session II: Productivity Estimates for Sectors in Indian economy) for the smooth conduct of the sessions and for providing comments on several important research issues. To Dr. Simrit Kaur (University of Delhi), Dr Laveesh Bhandari (Indicus Analytics), Dr. S.K. Das (CSO), Shri. G. C. Manna (CSO) and Dr. Sandeep Sarkar (IHD), warm appreciation for comments in the capacity of discussants on various aspects of the construction of variables.
Dr. Subir Gokarn (then Deputy Governor, RBI) and Shri Deepak Mohanty (Executive Director, RBI) provided comments on important aspects of the research along with others at the presentations made at the RBI, Mumbai in 2011 as well as in 2012.We express our sincere gratitude to them for their valuable contributions on various aspects of the research. We would also like to express our thanks to officers of the RBI who were present at these workshops. The team wishes to thank all participants at the several workshops/seminars, which included academics, policymakers, researchers and officials of statistical agencies (CSO, NSSO and ASI) and the Reserve Bank of India. Finally, we would like to express special thanks to Shri Ramesh Kolli (formerly CSO) for extensive consultation on several pertinent methodological issues during the construction of the dataset of India KLEMS.
We would also like to thank the Central Statistical office (CSO), Government of India for providing several datasets, especially those pertaining to the construction of capital services by asset type and soft copies of Input-Output tables not available in the public domain for the research. In particular, we express our gratitude to officers of the National Accounts Division (NAD) and the Computer Centre of the CSO for their help and advice on many data nuances. In particular, we thank Shri P.C. Mohanan, Shri P. C. Nirala, Ms T.Rajeswari and Ms Anindita Sinharoy.
We would also like to thank senior officers of the RBI—Smt. Balbir Kaur, Shri S.V. Arunachalaramanan and Smt. Rekha Mishra—for constructive suggestions in the co-ordination meetings. We also express our sincere thanks to Shri Ashish Kumar (CSO) and Shri. S. V. Ramanamurthy (CSO) for many helpful comments and suggestions at the co-ordination meetings.
We would like to express our gratitude to our referees, Dr.Isher Ahluwalia, Professor T. N. Srinivasan, Professor K. Sundaram and Dr. Ashok Gulati, for their helpful advice and comments on an earlier draft of the report from which the report has benefitted significantly. We would also like to thank the members of the Advisory Committee for their helpful suggestions during the research, especially Professor Dale Jorgenson, Professor Marcel Timmer, Dr. Bart Van Ark and Professor Mary O’ Mahony. We like to express our gratitude to Dr. Isher Ahluwalia for her support to the project. Finally, a special mention of Professor K. L. Krishna, chairman, Advisory Committee, India KLEMS project has to be made for his valuable leadership and guidance at all stages of the project. He has commented extensively on several drafts of all chapters in the report.
Finally, we thank the administrative and finance departments of ICRIER for their support throughout the first and second phase of the project. In particular, special mention of the team of Shri Manmeet Ahuja and Shri Krishan Kumar at ICRIER for help in organising workshops, co-ordination meetings and other research meetings. The report was formatted, typeset and printed by Shri Raj Kumar Shahi at ICRIER.
Finally, comments and suggestions on the report are welcome.
Bibliography
Acharya, Shankar, IsherAhluwalia, K. L. Krishna and IlaPatnaik (2003), ‘India: Economic growth, 1950-2000’, Global research project on growth, Indian Council for Research on International Economic Relations, New Delhi.
Aggarwal, Suresh Chand (2004), Labour quality in Indian manufacturing: A state level analysis, Economic and Political Weekly, 39(50), pp.5335-44.
Aggarwal, Suresh Chand (2010), ‘Measuring labour input in India- A sectoral perspective’ First World KLEMS Conference, Harvard University, August.
Aghion, Philipe and Robin Burgess (2003), ‘Liberalization and industrial performance: Evidence from India and the UK,’(available online at www.ycsg.yale.edu/activities/files/Aghion-Burgess Paper.pdf, accessed September 24, 2010).
Ahluwalia, I.J. (1985), Industrial growth in India. Stagnation since the mid-sixties, New Delhi: Oxford University Press.
Ahluwalia, I.J. (1991), Productivity and growth in Indian manufacturing, New Delhi: Oxford University Press.
Ahluwalia, Montek S. (1994), ‘India’s economic reforms’, Address at a Seminar on India’s Economic Reforms at Merton College, Oxford, June.
Ahluwalia, Montek S. (2002), ‘Economic reforms in India since 1991: Has gradualism worked?’Journal of Economic Perspectives, 16(3), 67-88.
Alivelu, G. (2006), Analysis of productivity and costs across the Indian zonal railways 1981-82 to 2002-03, unpublished Ph.D. thesis, Centre for Economic and Social Studies and Dr. B.R. Ambedkar Open University, Hyderabad.
Ana M. Fernandes and Ariel Pakes (2009),‘Evidence of underemployment of labour and capital in Indian manufacturing’, in EjazGhani and Sadiq Ahmed(Eds.), Accelerating growth and job creation in South Asia, New Delhi: Oxford University Press.
Arrow, K. J. (1972), ‘The measurement of real value added’,Institute for Mathematical Studies in the Social Sciences.
Avila, A.F. D. and R.E. Evenson (2004a), ‘TFP calculation from FAO data’, unpublished.
Avila, A.F.D. and R.E. Evenson (2004b), ‘Total factor productivity growth in agriculture: The role of technological capital,’ Yale Economic Growth Center, New Haven, CT.
Azeez E. A (2005) ‘Domestic capacity utilisation and import of capital goods: Substitutes or complementary? Evidence from Indian capital goods sector’, in S. Tendulkar, Mitra, Narayanan and Das (Eds.), India: Industrialisation in a reforming economy- Essays for K.L Krishna, New Delhi: Academic Foundation.
Balakrishnan, P. and K. Pushpangadan (1994), ‘Total factor productivity growth in manufacturing industry: A fresh look,’ Economic and Political Weekly, July 13, 29, pp. 2028-35.
Balakrishnan, Pulapre and K. Pushpangadan (1998), ‘What do we know about productivity growth in Indian industry,’Economic and Political Weekly, August 15-22, 33, pp. 2241-46.
Balakrishnan, Pulapre, K. Pushpangadan and M. Suresh Babu (2000), ‘Trade liberalisation and productivity growth in manufacturing: Evidence from firm level panel data’, Economic and Political Weekly, Oct 7, pp. 3679-3682.
Balakrishnan, Pulapre and M. Parameswaran (2007), ‘Understanding economic growth in India, Further observations’, Economic and Political Weekly, November 3.
Banerjee,Asit (1975), Capital intensity and productivity in Indian industries, New Delhi: Macmillan.
Banga, Rashmi (2005), ‘Critical issues in India’s services led growth’, ICRIER Working Paper No. 171, Indian Council for Research on International Economic Relations, New Delhi.
Banga, Rashmi and BishwanathGoldar (2007),‘Contribution of services to output growth and productivity in Indian manufacturing: Pre- and post-reforms,’Economic and Political Weekly, 42(26): 2769-77.
Basu, Kaushik and AnnemieMaertens (2007), ‘The pattern and causes of economic growth in India’,BREAD Working Paper No. 149.
Basu,Kaushik and AnnemieMaertens (2009), ‘The growth of industry and services In South Asia’, in EjazGhani and Sadiq Ahmed(Eds), Accelerating growth and job creation In South Asia, New Delhi: Oxford University Press.
Basu, S., J. Fernald, N. Oulton and S. Srinivasan (2003), ‘The case of the missing productivity growth: Or, does information technology explain why productivity accelerated in the United States but not the United Kingdom?’NBER Macroeconomics Annual.
Besley, Tim and Robin Burgess (2004), ‘Can labour regulation hinder the growth of industry and services in South Asia economic performance? Evidence from India’, Quarterly Journal of Economics, 119(1): 91–134.
Bhalla,Surjit S. and TirthatanmoyDas (2005),‘Pre- and post-reform India: A revised look at employment, wages and inequality’, India Policy Forum, Vol. 2, NCAER, New Delhi.
Bhattacharjea, Aditya (2008), ‘India’s economic growth dissected’, Economic and Political Weekly, October 11.
Bhaumik, S. K., S. Gangopadhyay and S. Krishnan (2006), ‘Reforms, entry and productivity: Some evidence from the Indian manufacturing sector’, Indian Development Foundation Working Paper No. 0602 and IZA Discussion Paper No. 2086.
Bollard, A., P.J. Klenow and Gunjan Sharma (2011), ‘India’s mysterious manufacturing miracle’, July 2011 version, available online at:http://klenow.com/BKS_IMMM.pdf (accessed August 26, 2011).
Bosworth, Barry and AnnemieMaertens (2010), ‘Economic growth and employment generation: The role of the service sector’, in EjazGhani (Ed.), The service revolution in South Asia, New Delhi: Oxford University Press.
Bosworth B., S. Collins and A. Virmani (2007), ‘Sources of growth in Indian economy’,NBER Working Paper No. 12901.
Bosworth, Barry and Susan M. Collins (2008), ‘Accounting for growth: Comparing China and India,’Journal of Economic Perspectives, 22(1): 45-66.
Brahmananda, P. R. (1982), Productivity in the Indian economy: Rising Inputs for falling outputs, Himalaya Publishing House.
Chaddha, G. K (2003), ‘Issues in employment and poverty’, Discussion Paper 7, Recovery and Reconstruction Department, International Labour Office, Geneva.
Christensen, L.R. and Jorgenson D.W. (1969), ‘The measurement of US real capital input, 1929-1967’, Review of Income and Wealth, 15, 293-320.
CMIE (2011), Energy, Economic Intelligence Services, Centre for Monitoring Indian Economy, Mumbai.
Colecchia A. and P. Schreyer (2001), ‘ICT investment and economic growth in the 1990s: Is United States a unique case’, OECD STI Working Papers, pp 1-31.
Corrado, Carol, and Lawrence Slifman (1999), Decomposition of productivity and unit costs. American Economic Review, 89(2): 328-332.
CSO (2007), Chapter 33, ‘Factor incomes’, in National Accounts Statistics: Sources and Methods, Central Statistical Organisation, Ministry of Statistics and Programme Implementation, Government of India.
CSO (2007), ‘National Accounts Statistics: Sources and methods’, available at http://mospi.nic.in/ Central Statistical Organization: Population of India, different years.
Das, Deb Kusum (2004), ‘Manufacturing productivity under varying trade regimes, 1980-2000’,Economic and Political Weekly, 39(5): 423-33.
Das, Deb Kusum (2006) ‘Improving Industrial productivity: Does trade liberalization matter? Evidence from Indian capital and intermediate goods sectors’ in S. Tendulkar, Mitra, Narayanan and Das (Eds.), India: Industrialisation in a reforming economy Essays for K.L. Krishna, New Delhi: Academic Foundation.
Das, Deb Kusum and Gunajit Kalita (2009), ‘Aggregate productivity growth in Indian manufacturing: An application of Domar aggregation’, Working Paper no.239, Indian Council for International Economic Relations, New Delhi.
Das, Deb Kusum and A. A. Erumban (2010), ‘Capital services estimates for Indian economy: A sectoral perspective’, First World KLEMS Conference, Harvard University, August.
De Long, Bradford J. (2003), ‘India since Independence: An analytic growth narrative’, in DaniRodrik (Ed.), In search of prosperity: Analytic narratives on economic growth, NJ: Princeton University Press.
De Long, Bradford J. and L. Summers (1991), ‘Equipment investment and economic growth’, The Quarterly Journal of Economics, 106(2): 445-502.
deVries, G., N. Mulder, M. Dal Borgoand A. Hofman (2007), ‘ICT investment in Latin America: Does IT matter for economic growth?’ Presentation to SeminarioCrecimiento, Productividad y Tecnologías de la Información March 29– 30, 2007.
De, P.K. (2004), ‘Technical efficiency, ownership and reform: An econometric study of Indian banking industry’, Indian Economic Review, Special Issue on Productivity and Efficiency, 39 (1) (Jan-June).
Denison, Edward F. (1957), ‘Theoretical aspects of quality change, capital consumption and net capital formation’ in Problems of capital formation, NBER.
Denison, Edward F. (1962), ‘The sources of economic growth in the United States and the alternatives before US’. Supplementary paper 13, New York: Committee for Economic Development.
Dholakia, B. (1974), Sources of economic growth in India, Baroda: Good Companion
Dholakia, B. (2002), ‘Sources of India’s accelerated growth and the vision of the Indian economy in 2020’, Indian Economic Journal,49(4).
Diewert, W.E. (1976), ‘Exact and superlative index numbers’, Journal of Econometrics, 4, 115-145.
Diewert, E (1980), ‘Aggregation problems in the measurement of capital’, in D. Usher (Ed.), The measurement of capital, Chicago, The University of Chicago Press.
Diewert, W.E. (1982), ‘Superlative Index numbers and consistency in aggregation,’Econometrica, 46, 883-900.
Dougherty, S.M., R. Herd and T.Chalaux (2009), ‘What is holding back productivity growth in India? Recent micro evidence,’OECD Journal: Economic Studies, (1).
Eichergreen, Barry and Poonam Gupta (2009), ‘The service sector as India’s road to economic growth?’ICRIER Working Paper No. 249.
Erumban, Abdul Azeez (2008), ‘Capital aggregation and growth accounting: A sensitivity analysis’, EU KLEMS working paper 24.
Erumban, Abdul Azeez (2008a) ‘Rental prices, rates of return, capital aggregation and productivity: Evidence from EU and US’, CESifo Economic Studies, 3(54):499-533.
Erumban, Abdul Azeez (2008b), ‘Measurement and analysis of capital, productivity and economic growth’, SOM theses series, University of Groningen (available http://irs.ub.rug.nl/ ppn/315102683).
Evenson, R.E., C. Pray and M.W. Rose Grant (1999), ‘Agricultural research and productivity growth in India’, Research Report No. 10, International Food Policy Research Institute, Washington, D.C.
Fan, S., P.B.R. Hazell and S. Thorat (1999), ‘Linkages between government spending, growth, and poverty in rural India’, Research Report No. 110. International Food Policy Research Institute, Washington, D.C.
Fosgerau, Mogenset al. (2002): ‘Measuring educational heterogeneity and labor quality: A note,’Review of Income and Wealth, 48 (2): 261-69.
Ghate, C., S. Wright and F. Tatiana (2010), ‘India’s growth turn around’ in KaushikBasu and A.Maertens (Eds.), Concise Oxford Companion to Economics, New Delhi: Oxford University Press.
Goldar, B.N. (1986a), Productivity growth in Indian industry, New Delhi: Allied Publishers.
Goldar, B.N. (1986b), ‘Import substitution, industrial concentration and productivity growth in Indian manufacturing’, Oxford Bulletin of Economics and Statistics, 48(2): 143-64.
Goldar, B.N. (2002), ‘TFP growth in Indian manufacturing in the 1980s’, Economic and Political Weekly, 37(49): 4966-68.
Goldar, B.N. (2004), ‘Indian manufacturing: Productivity trends in manufacturing in pre- and post-reform periods’, Economic and Political Weekly, 39(46/47): 5033-43.
Goldar, B.N. (2011) ‘Growth in organised manufacturing employment in recent years’, Economic and Political Weekly, 46(7), February 12.
Goldar, B. N. (2011), ‘Productivity in Indian manufacturing in the post-reform periods’, Institute of Economic Growth (IEG), New Delhi. Paper presented at the Workshop on Economic Reforms and the Evolution of Productivity in Indian Manufacturing, IIT Bombay, March 18-19.
Goldar, B.N. (2011), ‘Energy Intensity of Indian manufacturing firms: Effect of energy prices, technology and firm characteristics,’ Science Technology Society, 16 (3): 351-372.
Goldar, B.N.and Anita Kumari (2003), ‘Import liberalisation and productivity growth in Indian manufacturing industries in the 1990s,’Developing Economies, 41(4): 436-60.
Goldar, B.N.and Arup Mitra (2002), ‘Total factor productivity growth in Indian industry: A review of studies’ in B.S. Minhas (Ed.),National Income Accounts and Data Systems, New Delhi: Oxford University Press.
Goldar, B.N. and Arup Mitra (2008), ‘Productivity increase and changing sectoral composition: Contribution to economic growth in India’, IEG Working Paper E/291/2008, Institute of Economic Growth, Delhi.
Goldar, B.N. and Arup Mitra (2010), ‘Productivity Increase and changing sectoral composition: Contribution to economic growth in India’ in Pulin B. Nayak, BishwanathGoldar and PradeepAgrawal (Eds.) India’s economy and growth: Essays in honour of V.K.R.V.Rao, New Delhi: Sage.
Goldar, B.N and Renganathan, V.S (2008), ‘Import penetration and capacity utilization in Indian industries’, Working Paper no. E/293/2008, Institute of Economic Growth, Delhi.
Gollin,D.(2002). ‘Getting income shares right’, Journal of Political Economy, 110(2).
Guha-Khasnobis, Basudeb and Faisal Bari (2003), ‘Sources of growth in South Asian countries’, in Isher Judge Ahluwalia and John Williamson (Eds.), The South Asian experience with growth, Oxford University Press.
Gullickson, William(1995),‘Measurement of productivity growth in U.S. manufacturing’, Monthly Labour Review 118(7): :13-37.
Gullickson, William and Michael J. Harper (1987), ‘Multifactor productivity U.S. manufacturing, 1949-83’, Monthly Labour Review,110:18-28.
Harper, M.J., E.R. Berndt and D.O. Wood (1989), ‘Rates of return and capital aggregation using alternative rental prices’, in D.W. Jorgensonand R. Landau (Eds.), Technology and capital formation, MIT Press.
Hashim, B.R. and M.M. Dadi (1973), Capital-output relations in Indian manufacturing (1946-64), MS University, Baroda.
Hashim, Danish A. (2003), ‘A comparative analysis of productivity and cost in Indian Airlines; 1964-99,’Institute of Economic Growth, Delhi. Available online at: http://iegindia.org/dis_hash_67.pdf, accessed September 30, 2010.
Hashim, Danish A. (2004), ‘Cost &productivity in Indian textiles: Post MFA implications,’ ICRIER Working Paper No. 147, Indian Council for Research on International Economic Relations, New Delhi.
Hashim, Danish A., Ajay Kumar, and A. Virmani (2009), ‘Impact of major liberalization on productivity: The J Curve hypothesis’, Working Paper no. 5/2009-DEA, Ministry of Finance, Government of India.
Hassan, Rana, DevashishMitra and K. V. Ramaswamy (2003), ‘Trade reforms, labour regulations and labour demand elasticities: Empirical evidence from India’, Working Paper 9879, National Bureau of Economic Research, Cambridge MA.
Ho, Mun S., and Dale W. Jorgenson (1999): ‘The quality of the U.S. Workforce, 1948-95,’ manuscript, Harvard University.
Hulten, C.R. (1990), ‘The measurement of capital’, in E.R. Berndt and J.E. Triplett (Eds.), Fifty years of economic measurement, Studies in Income and wealth (pp. 119-152). Chicago: Chicago University Press.
Jorgenson, D.W (1963), ‘Capital theory and investment behavior’, American Economic Review, 53 (2): 247-259.
Jorgenson, D.W. (1989), ‘Capital as a factor of production’, in D.W.Jorgensonand Ralph Landau (Eds.), Technology and capital formation, Cambridge MA: MIT Press.
Jorgenson D.W. (2001), ‘Information technology and the U.S. economy’, American Economic Review, 91(1): 1-32.
Jorgenson, D.W. (2009), ‘A new architecture for the U.S. national accounts’, Review of Income and Wealth, 55(1): 1–42.
Jorgenson D.W. and K.J. Stiroh (2000), ‘Raising the speed limit: U.S. economic growth in the information age’, Brookings Papers on Economic Activity, (1):125-211.
Jorgenson, D.W. and K. Vu (2005), ‘Information technology and the world economy’, Scandinavian Journal of Economics 107(4): 631–650.
Jorgenson, D. W., M.S. Ho, and K. J. Stiroh(2005), Information technology and the American growth resurgence, Cambridge MA: MIT Press.
Jorgenson, D.W and Z. Griliches (1967), ‘The explanation of productivity change’, Review of Economic Studies, 34, 249-283.
Jorgenson, D.W. etal. (1987), Productivity and US economic growth, Cambridge MA: Harvard University Press.
Joshi, P.K., L. Joshi, R.K. Singh, J. Thakur, K. Singh, and A.K. Giri (2003), ‘Analysis of productivity changes and future sources of growth for sustaining rice-wheat cropping system’. National Agricultural Technology Project ((PSR 15; 4.2), National Centre for Agricultural Economics and Policy Research (NCAP), New Delhi, August.
Joshi, P.K., L. Joshi, R.K. Singh, J. Thakur, K. Singh, and A.K. Giri(2006), ‘Politics of economic growth in India, 1980-2005 – Part II: the 1990s and
‘Institutions and markets in India’s development: Essays for K.N.RAJ’by A.Vaidyanathan and K.L. Krishna, Oxford University Press, 2007 and Post reform period an Analysis at Company level’. In Proceedings Examining Ten Years of Economic Reforms in India. ANU, Canberra, Australia.
Kathuria V., R. Raj, and K. Sen (2010) ‘Organised versus unorganised manufacturing performance in the post-reform period’, Economic and Political Weekly, Volume 45(24).
Kim, J.I. and L.J. Lau (1994), ‘The sources of economic growth of the East Asian newly industrialized countries’, Journal of Japanese and International Economies, 8,235-271.
King, R.G and Ross Levine (1993), ‘Finance, entrepreneurship and growth: Theory and evidence’, Journal of Monetary Economics, 32, 513-542.
Kochhar Anjiniet al. (2006), ‘India’s pattern of development: What happened? What follows?’, Working Papers WP No. 06/22, International Monetary Fund.
Kochhar, K., U. Kumar, R. Rajan, A. Subramanian, and I. Tokatlidis, (2006), ‘India’s pattern of development: What happened, what follows?’Journal of Monetary Economics, 53(5): 981-1019.
Kohli, Atul (2006a), ‘Politics of Economic growth in India, 1980-2005 – Part I: The 1980s’, Economic and Political weekly, April 1.
Kohli, Atul (2006b), ‘Politics of Economic growth in India, 1980-2005 – Part I: The 1980s and Beyond’, Economic and Political Weekly, April 8.
Krishna, Raj and S.S. Mehta (1968). ‘Productivity trends in large scale industries’, Economic and Political Weekly, 3(43): 1655-60.
Krishna, K.L. (1987), ‘Industrial growth and productivity in India’ in P.R. Brahmananda and V.R. Panchamukhi (Eds.), The development process of the Indian economy, Bombay: Himalaya.
Krishna, K.L. (2006), ‘Some aspects of total factor productivity in Indian agriculture’ in R. Radhakrishnaet al.(Eds.), India in a globalising world, Essays in honour of C.H. HanunmanthaRao, New Delhi: Academic Foundation.
Krishna, K.L. (2007), ‘What do we know about the sources of economic growth in India?’ in A.Vaidyanathan and K.L. Krishna (Eds.), Institutions and markets in India’s development: Essays for K.N.Raj, New Delhi: Oxford University Press.
Kumar, Praduman and Surabhi Mittal (2006), ‘Agricultural productivity trends in India: Sustainability issues’, Agricultural Economics Research Review, 19: 71-88.
Kumar, Praduman, Surabhi Mittal, and MahabubHussain (2008), ‘Agricultural growth accounting and total factor productivity in South Asia: A review and policy implications’, Agricultural Economics Research Review, 21: 145-172.
Kumar, Rajiv and AbhijitSengupta (2008), ‘Towards a competitive manufacturing sector’, ICRIER working paper 203, New Delhi.
Kumari, A., (2001), ‘Productivity growth in Indian engineering industries during pre reform and post reform period: An analysis at company level’, in S. Tendulkar,Mitra, Narayanan and Das(Eds.), India: Industrialisation in a reforming economy: Essays for K.L. Krishna, New Delhi: Academic Foundation.
Manna, G.C (2010), ‘Current status of industrial statistics in India: Strengths and weakness’, Economic and Political Weekly, 45(46): 67-76.
Mathur, Somesh (2007), ‘Indian IT and ICT industry: A Performance Analysis Using Data Envelopment Analysis and Malmquist Index’, Global Economy Journal, 7(2).
Mitra, Arup, AristomeneVaroudakis and Marie-AngeVeganzones-Varoudakis, ‘Productivity and technical efficiency in Indian States’ manufacturing: The role of infrastructure,’Economic Development and Cultural Change, 50(2): 395-426.
Mitra, Arup, Chandan Sharma and Marie-AngeVeganzones-Varoudakis (forthcoming), ‘Estimating impact of infrastructure on productivity and efficiency of Indian manufacturing’, Applied Economics Letters, 19(8): 779-83.
Mohan Rao, J. (1996), ‘Manufacturing productivity growth: Method and measurement,’Economic and Political Weekly, 31(44):2927-36.
Mohan, Rakesh (2008), ‘Growth record of the Indian economy, 1950-2008: A Story of sustained savings and investment’, Economic and Political Weekly, May 10.
Mukherjee, Anit N. and Yoshimi Kuroda (2003), ‘Productivity growth in Indian agriculture: Is there evidence of convergence across states?’Agricultural Economics, 29: 43–53.Policy Issues’,Indian Journal of Labour Economics, 47(4), 913-27, 2004
Nag, Tirthankar (2010), ‘Captive generation in India: The dilemma of dualism,’ India Infrastructure Report.
Nagaraj, R. (2008), ‘India’s recent economic growth: a closer look’, Economic and Political Weekly, April 12.
National Sample Survey Organisation, Employment and unemployment in India, various reports.
Nehru V. and A. Dhareshwa (1993), ‘New estimates of total factor productivity growth for developing and industrial countries’, Policy Research Working Paper Series, No 1313, World Bank.
O’Mahony, M. and M.P. Timmer (2009), ‘Output, input and productivity measures at the industry level: The EU India KLEMS database’, Economic Journal, 119(538): F374-F403.
OECD (2001),OECD productivity manual, Paris.
OECD (2009), ‘Measuring capital – OECD manual: Measurement of capital stocks, consumption of fixed capital and capital services’. Second Edition, OECD, Paris.
Panagariya, Arvind, (2008), India the emerging giant, New York: Oxford University.
Papola, T.S. and ParthaPratimSahu(2012), ‘Growth and structure of employment In India: Long-term and post-reform performance and the emerging challenge’, Institute for Studies in Industrial Development, New Delhi.
Pattnayak, SanjaSamirana and Shandre M. Thangavelu (2009), ‘Economic liberalization in India: Productivity and learning-by-export’, CCAS working paper no. 21, Center for Contemporary Asian Studies, Donisha University.
Pradhan, G. and K. Barik (1998), ‘Fluctuating total factor productivity in India: Evidence from selected polluting industries,’ Economic and Political Weekly, February 28, 33: M25-M30.
Prakash, B.S. (2004), ‘Structural change and productivity trends in unorganised manufacturing sector 1984-2001’, IAMR Report No. 2.
Pratt, A.N., B. Yu and S. Fan (2008), ‘The total factor productivity in China and India: New measures and approaches’, China Agricultural Economic Review, 1(1): 9-22.
Puja VasudevaDutta (2004), The structure of wages in India, 1983-1999, PRUS Working Paper Industry in India ArthaVijnana, 4.
Rangarajan, C. (2009),India monetary policy, financial stability and other essays, New Delhi: Academic Foundation.
Rao, D.S.P. and T.J. Coelli (2004), ‘Catch-up and convergence in global agricultural productivity’, Indian Economic Review, 39 (1): 123-48.
Ray, Subhash C. (2002), ‘Did India’s economic reforms improve efficiency and productivity? A nonparametric analysis of the initial evidence from manufacturing,’ Indian Economic Review, 37(1): 23-57.
Raychaudhuri, B. (1996), ‘Measurement of capital stock in Indian industries’, Economic and Political Weekly, May 25.
Reddy, M.G. K. and S.V. Rao (1962), ‘Functional distribution in the large scale manufacturing sector in India’, ArthaVijnana, 4(3):189-96.
Rodrik, Dani, and Arvind Subramanian (2005), ‘From ‘Hindu growth’ to productivity surge: The mystery of the Indian growth transition,’ IMF Staff Papers, vol. 52, No.2.
Sailaja, M. (1988), Productivity in the service sector: The case of Indian Railways, 1950-51 to 1985-86, unpublished Ph.D. thesis, Delhi School of Economics, Delhi.
Schreyer, P. (2002), ‘Computer price indices and international growth comparisons’, Review of Income and Wealth.
Sen, Kunal (2009), ‘Trade policy, inequality and performance in Indian manufacturing’, London: Routledge.
Shetty, S. L. (2006),‘ Savings and investment estimates: Time to take a fresh look’, Economic and Political Weekly, February 12, pp. 606-610.
Sinha, Ram Pratap (2007), ‘Premium Income of Indian life insurance industry: A total factor productivity approach’, IUP Journal of Financial Economics, 5(1): 61-69.
Sinha, Ram Pratap and BiswajitChatterjee (2008), ‘Fund-based activity of Indian commercial banks: A Malmquist approach,’Indian Economic Review, 43(1): 83-102.
Sivadasan, Jagadeesh (2008), ‘Barriers to competition and productivity: Evidence from India’ available online at
http://webuser.bus.umich.edu/jagadees/papers/pml_dec08_all.pdf, accessed September 30, 2010.
Sivasubramonian, S. (2004), The sources of economic growth in India: 1950-51 to 1999-2000, New Delhi: Oxford University Press.
Srinivasan, T.N. (2005), ‘India’s statistical system: Critiquing the report of the National Statistical Commission’, in Angus Deaton and Valerie Kozel (Eds.), The great Indian poverty debate, New Delhi: Macmillan.
Srinivasan, T. N. (2008): ‘Employment and unemployment since the early 1970’s’, India Development Report, Mumbai: Oxford University Press.
Srinivasan, T.N. and Suresh D. Tendulkar (2003), Reintegrating India with the world economy,New Delhi: Oxford University Press.
Srivastava, Vivek (1996), Liberalisation, productivity and competition: A panel study of Indian manufacturing, Delhi: Oxford University Press.
Srivastava, Vivek, Pooja Gupta and ArindamDatta (2001), The impact of India’s economic reforms on industrial productivity, efficiency and competitiveness: A panel study of Indian companies, 1980-97, Report, National Council of Applied Economic Research, New Delhi.
Subramanian, Arvind (2008), India’s turn: Understanding the economic transformation, New Delhi: Oxford University Press.
Sundaram, K. (2007): Employment and poverty in India, 2000-2005, Economic and Political Weekly, Vol. 42(30): 3121-31.
Sundaram, K. (2009), ’Measurement of employment and unemployment in India: Some issues’, Working Paper No. 174, Centre for Development Economics, Department of Economics, Delhi School of Economics, Delhi.
Timmer,Marcel P.and B. van Ark (2005), ‘Does information and communication technology drive EU-US productivity growth differentials?’ Oxford Economic Papers, 57(4): 693-716.
Timmer, Marcel P., Robert Inklaar, Mary O’Mahony and Bart van Ark (2010), Economic growth in Europe: A comparative industry perspective, Cambridge: Cambridge University Press.
Topalova, Petia (2004), ‘Trade liberalization and firm productivity: The case of India’, IMF Working Paper, International Monetary Fund.
Topalova, Petia and AmitKhandelwal (2010), ‘Trade liberalization and firm productivity: The case of India’, Review of Economics and Statistics, posted online August 2010.
Trivedi, Puspa, A. Prakash, and D. Sinate (2000), ‘Productivity in major manufacturing industries in India: 1973-74 to 1997-98,’ Development Research Group Study no. 20, Department of Economic Analysis and Policy, Reserve Bank of India, Mumbai.
Trivedi, Puspa, L. Lakshmanan, Rajeev Jain and Yogesh Kumar Gupta (2011), ‘Productivity, efficiency and competitiveness of the Indian manufacturing sector’, Development Research Group, Study no. 37, Department of Economic and Policy Research, Reserve Bank of India.
Unel, Bulent (2003), ‘Productivity trends in India’s manufacturing sectors in the last two decades’, IMF Working Paper No WP/03/22.
Unni, Jeemol, N. Lalitha, and UmaRani (2001), ‘Economic reforms and productivity trends in Indian manufacturing,’Economic and Political Weekly, 36(41): 3914-3922.
vanArk, B., M. O’Mahony and M.P. Timmer (2008), ‘The productivity gap between Europe and the U.S.: Trends and causes’, Journal of Economic Perspectives, 22(1), 25-44.
Varma, Rubina (2008), ‘The service sector revolution in India’, Research Paper no. 2008/72, UNU-WIDER.
Veeramani, C. and BishwanathGoldar (2005), ‘Manufacturing productivity in Indian states: Does Investment climate matter?’Economic and Political Weekly, 40(24): 2413-20.
Virmani A. (2004), ‘Sources of India’s economic growth’, ICRIER Working Paper No. 131, Indian Council for Research on International Economic Relations, New Delhi.
Virmani, Arvind and Danish A. Hashim (2011), ‘J-Curve of productivity and growth: Indian manufacturing post-liberalization’ IMF Working Paper, WP/11/163.
Visaria, P. (1996), ‘Structure of Indian workforce, 1961-1994’, Indian Journal of Labour Economics, pp.725-739.
Wadhwa, D. (2010), ‘Construction of gross value added series: A study of 31 KLEMS industries in India’, Paper presented at the workshop on Economic Growth in India, University of Groningen, Groningen April.
Williamson, John and Roberto Zagha (2002), ‘From Slow growth to slow reform’, Institute for International Economics, Washington.
Young, A.(1992), ‘A tale of two cities: Factor accumulation and technical change in Hong Kong and Singapore’, Macro Economics Annual,NBER13-54.
|