Issued for Discussion DRG Studies Series Development Research Group (DRG) has been constituted in Reserve Bank of India in its Department of Economic and Policy Research. Its objective is to undertake quick and effective policy-oriented research backed by strong analytical and empirical basis, on subjects of current interest. The DRG studies are the outcome of collaborative efforts between experts from outside Reserve Bank of India and the pool of research talent within the Bank. These studies are released for wider circulation with a view to generating constructive discussion among professional economists and policy makers. Responsibility for the views expressed and for the accuracy of statements contained in the contributions rests with the author(s). There is no objection to the material published herein being reproduced, provided an acknowledgement for the source is made. DRG Studies are published in RBI website only and no printed copies will be made available. Director
Development Research Group |
Threshold Level of Inflation – Concept and Measurement Ravindra H. Dholakia
Jai Chander
Ipsita Padhi
Bhanu Pratap Abstract Threshold inflation that maximizes long-term growth in an economy is dependent on fiscal deficit (FD) and current account deficit (CAD). Since the existing empirical literature on threshold inflation lacks a robust theoretical framework, the present study considers the theory developed by Dholakia (2020) to estimate threshold inflation that maximizes steady state growth (SSG). Based on an appropriate degree of polynomial for investment rate and capital productivity with a cross-country data set of 58 countries for the period 1995 to 2018, the study broadly confirms higher threshold inflation with higher growth in emerging market economies as compared to the advanced economies. By introducing country-specific intercept and selected slope dummies, the study finds that the threshold inflation for India is around 6 per cent. An important finding of the study is that the long run trade-off between inflation and SSG is asymmetric such that a reduction in inflation rate leads to a much smaller gain in the long-term growth when inflation is higher than threshold compared to when inflation is lower and rises towards the threshold level. Also, the threshold inflation and corresponding growth are not unique for a country but depend on the other two parameters – FD/GDP and CAD/GDP. Policymakers may choose to set the inflation target below the threshold level only after considering the costs of sacrificing growth and implied poverty alleviation rate with likely benefits in terms of the distributional and financial stability implications which are not examined in this study. JEL Codes – C30, E31, E58, E60, O11, O42. Keywords – Inflation Targeting, Macroeconomic Policy, Inflation Growth, Threshold Inflation, Cross-country Panel.
Acknowledgement The authors are grateful to RBI for supporting the study through DRG Studies. Views expressed here are those of the authors and not of the organizations they may belong. Authors are grateful to Shri Binod Bhoi, Dr. Harendra Behera (discussants) and other participants in the DEPR Study Circle seminar of the Reserve Bank of India for useful comments on the earlier draft of the paper. Authors are also grateful to an anonymous external referee for very detailed suggestions and generous comments on the study. All remaining errors and omissions are authors’ responsibility.
Executive Summary Macroeconomic management in a country requires fixing long-term targets for real growth, inflation rate, fiscal deficit (FD) and current account deficit on balance of payments (CAD) as proportion of GDP. Unless internally consistent targets for all these four macro parameters are set, the macroeconomic policies to achieve these targets individually would always result in shortfalls, sub-optimal outcomes and wastage of efforts and resources. They can be set consistently by considering the theory of growth and threshold inflation provided by Dholakia (2020), wherein the targets for FD/GDP and CAD/GDP are treated as exogenous policy parameters. The present study carefully examines the concept of threshold inflation and defines it to be the long run equilibrium rate of inflation that maximizes the steady state growth (SSG) within the relevant range of values. The present study considers Harrod’s (1948) warranted growth as obtained by the multiplication of the investment rate and the incremental output capital ratio (or capital productivity). Both these components of growth are then investigated through a literature review and plausible arguments to arrive at their respective determinants. Inflation rate, FD/GDP and CAD/GDP emerge as the major determinants of each of the two components of growth supported by the empirical verification. Since the relationship between the long run inflation rate and the SSG rate is not only non-linear but also non-monotonic as per the theory, it is pertinent to examine the precise functional form that can result in a stable threshold inflation and corresponding maximized SSG rate. Among the non-linear functional forms, polynomial functions are considered in the study to determine the most appropriate degree of polynomial for the relationship. By considering a cross-country data set for 58 countries for the period 1995 to 2018 that provides enough degrees of freedom to experiment with different degrees of freedom, the study finds that the appropriate functional form for the investment rate-inflation equation is a polynomial of degree two and for the capital productivity-inflation equation is a polynomial of degree one. Thus, the SSG-long run inflation equation is a polynomial of degree three, implying the existence of both growth maximizing and growth minimizing inflation rates in relevant ranges. Empirical findings of the study broadly confirm higher threshold inflation and higher growth in the emerging market economies than in the advanced economies. From the cross-country panel data, the study also derives estimates of the threshold inflation for India by introducing country specific intercept and selected slope dummies. It also provides estimates of the trade-off between long run inflation and SSG rate – 40bps of loss in growth per 100bps reduction in inflation from the threshold level; and 15bps of gain in the growth for 100bps reduction in inflation towards the threshold level. Thus, an important finding of the present study is that the trade-off between long run equilibrium inflation and SSG is not symmetric around the threshold inflation. When the inflation is higher than the threshold level, reduction in inflation rate leads to a much smaller gain in the long-term growth compared to when inflation is lower and rises towards the threshold level. Such long run trade-off along with the short to medium run sacrifice ratios for the country should be used for considering costs and benefits of setting inflation target in the country. Although the present study is based on the intercountry data estimates the threshold inflation for India at around 6 per cent, which is broadly similar to Dholakia (2020), it is suggested that the estimates based exclusively on the country data should be used for policy making in the country. However, the findings of the study clearly show that the threshold inflation and corresponding growth is not unique for a country but depends on the other two parameters – FD/GDP and CAD/GDP. If a country chooses the target values of FD/GDP and CAD/GDP to be achieved in the long run, its potential output growth gets determined through the corresponding value of threshold inflation. The policy makers may choose to set the inflation target below the threshold level, but only by consciously sacrificing long-term real growth of GDP and hence the adverse impact on the rate of poverty alleviation. On the other hand, lower inflation has favourable redistribution effects particularly on the poor and is beneficial for financial stability. These costs and benefits of fixing a long-term inflation target will thus have to be considered while making the choice. Financial stability concerns can be considered only by modifying and extending the theory of growth and threshold inflation proposed by Dholakia (2020), which has not been attempted in the present study.
Threshold Level of Inflation – Concept and Measurement 1. Introduction Macroeconomic management in any economy usually proceeds by setting targets of crucial aggregates to be achieved over specified time horizon of five to ten years. In most of the countries these aggregates are growth rate of real GDP, retail inflation rate, fiscal deficit (FD) to GDP ratio and current account deficit (CAD) on balance of payments to GDP ratio. In the latter half of the last century, these four targets were usually set by a single central authority in a country in consultation with different constituents. They were largely aspirational and therefore, the question about their internal consistency never arose. However, the principles and approach to macroeconomic management changed substantially after the crude oil shocks of the 1970s and the end of cold war in the late 1980s. Assigning different goals to different organs of the government to increase accountability and answerability became a more popular practice. Since fiscal and monetary policy are more precisely defined macroeconomic policies, the targets of FD/GDP and inflation rate were assigned respectively to the Ministry of Finance and the Central Bank of the country. Further, to monitor and make them accountable for their conduct, specific legislations were enacted by the Parliament. For instance, the Fiscal Responsibility and Budget Management (FRBM) Act was enacted for the Central Government and similar legislations were passed in every State Government in India during 2003 to 2010. Similarly, inflation targeting was formally adopted with the amendments to the Reserve Bank of India (RBI) Act, effective June 27, 2016. Under both these legislations, formal targets were set for FD/GDP ratio and inflation rate, respectively, to be achieved over a fairly long time period. Thus, out of the four targets for efficient macroeconomic management, only two targets – FD/GDP and inflation rate are clearly allotted and the remaining two are not so unambiguously allotted. To continue with the illustration of India, the Prime Minister had set the aspirational target of achieving a $5 trillion economy by 2024-25 implying a real growth of 8 per cent per annum over next 6 years (GoI, 2019). Although the CAD/GDP target is not formally set, it is considered prudent to restrict it to less than 3 per cent by most economists and analysts. Since all these targets are set by different organs of the government, they are set almost independently. Such a situation poses a serious challenge for efficient macroeconomic management and monitoring in a country. Moreover, it raises genuine concerns about internal consistency of the whole target setting exercise, because the formal enactment of these targets is invariably derived strictly by following partial methods. Unless these targets are set carefully and consistently by considering other targets in a holistic manner, the macroeconomic management and monitoring in a country cannot improve. In this context, the theory of growth and threshold inflation given by Dholakia (2020) provides a framework to effectively address this issue. At the time of setting the inflation target for the long run, the Central Bank of a country should consider the concept and appropriate measurement of threshold inflation rate that maximizes long-term real growth of the economy. In the present study, we examine the concept and measurement of threshold inflation in an international context by considering cross-country panel data for 1995-2018. In the next section, we examine the concept of threshold inflation with its roots in the inflation-unemployment (or growth) trade-off, optimal inflation and the time element involved. In the third section, we briefly survey the literature including empirical estimates of the threshold inflation. The fourth section then presents a structural multi-equation model and its operationalization to estimate the threshold inflation for an economy. The fifth section presents empirical results of our model using the cross-country panel data. The last section concludes the study with discussion on the implications of our findings for macroeconomic target setting. 2. Concept of Threshold Inflation The concept of threshold inflation is linked to the level of inflation beyond which it becomes detrimental to economic growth. However, since the theoretical framework for inflation is in terms of aggregate demand and supply, sometimes it gets unintentionally linked to the level of output rather than growth. This confusion arises because in the theory of income determination, introduction of aggregate supply side depends on the trade-off between inflation and unemployment, which is taken to be similar to a trade-off between the objectives of achieving low inflation and high growth. The Keynesian analysis of non-neutrality of money assumes that nominal wages are more rigid than prices. Increase in money resulting in higher price level, therefore, leads to a decrease in real wages that would bring about an improvement in real economic activity (Rangarajan, 1998). This was loosely interpreted to mean higher inflation resulting in higher growth. Similarly, the popular concept of overheating of an economy is obtained when the output exceeds the potential output thereby putting pressure on the labour and other factor markets ultimately pushing up the prices. Again, this is loosely interpreted to mean higher growth (than potential growth) leading to higher inflation. Even when the traditional aggregate demand and supply framework of output and prices is considered in its dynamic form, as suggested by Dholakia (2014a and 2014b), the dynamic aggregate demand and supply functions are in inflation and output gap and not in inflation and growth. The perspective on this trade-off has changed significantly over time with researchers estimating various levels of inflation rate which can be considered optimal for a given economy. The idea of ‘optimal inflation’ propounded by Bailey (1956) and Friedman (1969) was based on the intuition of private opportunity cost of holding money which is the nominal interest rate and the social marginal cost of printing money which can be considered as negligible. A wedge between the two costs would generate inefficiency to the extent that nominal interest rate is greater than zero. The optimal nominal interest rate should thus be equal to zero. In a steady state economy, this would require the inflation rate to be negative but numerically equal to real return on capital. Phelps (1973), however, argues that the distortions associated with taxation can be minimised by taxing everything at the same rate. Therefore, Friedman’s rule of zero nominal interest rate is not consistent with economic efficiency and there would be a need to tax liquidity by having a positive nominal interest rate and inflation to achieve efficiency in the economy. The subsequent literature, however, shows that Friedman’s rule of zero nominal interest rate for optimal inflation remains valid even without lump sum taxes under certain conditions (Chari, Christiano and Kehoe, 1996). Thus, the literature on optimal level of inflation or nominal interest rates seems divided. Also, the initial literature on the subject largely focussed on economic efficiency having implications for level of output, whereas the empirical literature on the threshold inflation attempted to identify the level of inflation which maximises growth of output over the long run. The arguments in favour of non-neutrality of money advanced the idea that output can be increased by increasing money supply and raising price level. This would reduce the real wages, assuming that wage setting takes into account higher prices with a lag and bring about an increase in output (Kannan and Joshi, 1998). Such an increase in output due to higher inflation and lower real wages, however, is more likely to be realised in the short- and medium-term and may not result in any meaningful improvement in output in the long run (Rangarajan, 1998). These arguments are based on the Phillips curve framework depicting the inflation-unemployment trade-off where inflation, reducing real wages, leads to increases in production. Lower inflation could be achieved only at the cost of lower output and higher unemployment. Such trade-offs, however, exist only during the short to medium term, because in the long run, as argued by Friedman (1968) and Phelps (1967), the Phillips curve is vertical and no trade-off between inflation and unemployment or output would exist. If we accept this argument, there would be nothing like threshold inflation. Alternatively, in this framework, threshold inflation could exist only if the long run Phillips curve is non-linear, yielding a backward-bending aggregate supply curve. On the other hand, the concept of threshold inflation is based on the long-term equilibrium inflation rate that maximizes the steady state rate of growth for the economy. Thus, the concept of “long run” involved in the threshold inflation is not the same as the one used in the trade cycle theory. The difference between the two lies in the analytical treatment of investment. The latter considers investment only as a component of aggregate demand in the system and abstracts out its capacity and production augmenting role, whereas the former explicitly treats investment as capacity and production augmenting factor of production. As a result, in the trade cycle theory, the potential output or “the full employment output” remains constant in the “long run” around which the short to medium term fluctuations are sought to be explained. On the contrary, in the steady state growth, the potential output is taken to grow at a constant rate. Therefore, the Phillips curve framework that pertains to the trade cycle theory is not appropriate for defining and measuring the threshold inflation. We must consider the growth theory framework for the purpose. The first formal growth model (Harrod, 1948) provided the steady state growth (SSG) solution as the natural growth rate, which is given by addition of the rates of growth of labour supply (n) and technical progress i.e. total factor productivity growth (TFPG), being equal to the warranted growth rate, which is given as multiplication of the desired investment rate (sd) and capital productivity (IOCR). Since Harrod (1948) treated all these four parameters as given constants for an economy, his steady state growth solution was unstable. The neo-classical growth theory provided a stable steady state growth solution in terms of exogenous factors such as technical progress (TFPG) and growth rate of labour supply (n). In an open economy, as argued by Dholakia (2020), however, both these factors are likely to be endogenous and not exogenous as argued by Harrod (1948) due to his assumption of a closed economy. In an open economy, the rate of inflation can become an important determinant of the steady state rate of growth. It can influence TFPG through its effect on investment and effectiveness of research and development expenditure (Briault, 1995). Similarly, by determining the cost of living and standard of life in a country, it can also impact the rate of in or out migration and hence the rate of growth of labour (n). Role of inflation in determining the growth path over long time horizon is particularly relevant for a developing economy. In this framework, the concept of threshold inflation could be effective only if the warranted growth rate is non-linearly related to inflation rate such that the second derivative is negative. As we see in the next section, there are good reasons and arguments in the literature to expect such a relationship between the warranted growth and inflation in any economy. The theory of growth and threshold inflation proposed by Dholakia (2020) shows that, in the absence of any intervention from the government and other exogenous factors, the warranted growth would always have a tendency to be at the maximum level corresponding to the threshold level of inflation and that the natural growth would adjust to the warranted growth in the steady state growth. Thus, the steady state growth would occur at the threshold inflation in an economy left to market forces. Since this is a base case, the government can avoid unnecessary adjustment costs in practice by targeting long-term inflation and growth respectively at the threshold inflation and steady state growth. At this stage, we treat FD/GDP and CAD/GDP targets as exogenously given. 3. Literature Review The discussion on literature is aimed at outlining the theoretical developments around inflation-growth association and also presenting the empirical estimates of threshold inflation in the international and in the Indian context. 3.1 Theoretical Literature The debate on the relationship between inflation and output/employment growth has been subject to rigorous theoretical and empirical work which was only bolstered with the empirical observation of a negative relationship between nominal wage growth and unemployment rate (Phillips, 1958). While the Phillips-curve was originally based on the UK macroeconomic data, Samuelson and Solow (1960) used the USA data and found an implied zero-inflation rate of unemployment to be around 3 per cent in the pre-World War-II years and about 5-6 per cent during the post-war years. This laid the ground for the analysis of exploitable trade-off that supposedly exists between inflation and unemployment. The natural rate hypothesis propounded in the works of Friedman (1968), Phelps (1968) and Lucas (1972) overturned the notion of trade-off between inflation and unemployment to monetary non-neutrality. Friedman and Phelps seek to explain inflation with the help of inflation expectations – assuming “adaptive” or “backward-looking” expectations. They posit that if in an economy, which is initially operating at its natural rate of unemployment and a consistent inflation rate, policymakers try to lower the unemployment rate by increasing inflation, agents adjust their inflation expectations upwards in the face of higher than anticipated inflation rate. This shifts the Phillips curve upwards till the actual unemployment rate returns to its natural rate. In this framework, inflation expectations are fully realised in the long run and the trade-off between inflation and unemployment exists only in the short run implying a vertical Phillips curve in the long run. This work also led to the conclusion that in the long run policymakers cannot choose any unemployment other than a ‘natural rate of unemployment’ that is dependent on the microeconomic structure of the labour and goods market. Thus, money could be non-neutral in the short run, but is neutral in the long run. Subsequently, some studies suggested the possibility of a negatively sloped Phillips curve even in the long run due to incomplete incorporation of inflation expectations in wage contracts (Tobin, 1972; Palley, 1994 and 1997). Akerlof et al. (2000) adopt a multi-agent approach to theoretically explain the possibility of a backward-bending Phillips curve. According to them, the Phillips curve in the long run, when actual and expected inflation rates are equal, is depicted as:  Their model allows agents to differ in terms of rationality such that some firms are “fully-rational” in anticipating inflation, while other firms tend to be “near-rational” and either ignore inflation or only partially account for it in their wage setting behaviour. More importantly, taking the suggestions from behavioural economics, they postulate that agents tend to ignore inflation when it is at a very low level while they account for it fully when it is at a higher level because the cost of ignoring it becomes too high. Accordingly, unemployment (u) is close to its natural rate (un) when inflation (π) is very low (or zero) or at a very high level. Unemployment declines below the natural rate when inflation increases above zero but remains low. As inflation increases further, the share of rational agents starts to increase reflecting higher pass-through of expected inflation into the nominal wage setting. At high rates of inflation, all agents tend to be fully rational and the natural rate of unemployment behaves as an asymptote in this case. This gives rise to a value of inflation that minimises unemployment and the Phillips curve is seen to be backward bending for a range around it, turning nearly vertical at very high values of inflation. Interestingly, for the US economy, they estimate the threshold level of inflation to be in the range of 1.5 to 4 per cent depending on the underlying price index used. Building on the earlier work on multi-sector incomplete incorporation of expectations model, Palley (2003, 2011) drew similar conclusion on the threshold level of inflation. When inflation is low, inflation expectations are also low and are not incorporated into wage setting. As inflation increases, inflation expectations also rise and are increasingly incorporated into wage-setting leading to a steepening of the Phillips curve. After a threshold level, “…the Phillips curve bends back because workers start to ratchet up their incorporation of inflation expectations faster than the increase in inflation”. At some high level of inflation, the Phillips curve would become vertical. Their model allows agents to differ in terms of rationality such that some firms are “fully-rational” in anticipating inflation, while other firms tend to be “near-rational” and either ignore inflation or only partially account for it in their wage setting behaviour. More importantly, taking the suggestions from behavioural economics, they postulate that agents tend to ignore inflation when it is at a very low level while they account for it fully when it is at a higher level because the cost of ignoring it becomes too high. Accordingly, unemployment (u) is close to its natural rate (un) when inflation (π) is very low (or zero) or at a very high level. Unemployment declines below the natural rate when inflation increases above zero but remains low. As inflation increases further, the share of rational agents starts to increase reflecting higher pass-through of expected inflation into the nominal wage setting. At high rates of inflation, all agents tend to be fully rational and the natural rate of unemployment behaves as an asymptote in this case. This gives rise to a value of inflation that minimises unemployment and the Phillips curve is seen to be backward bending for a range around it, turning nearly vertical at very high values of inflation. Interestingly, for the US economy, they estimate the threshold level of inflation to be in the range of 1.5 to 4 per cent depending on the underlying price index used. Building on the earlier work on multi-sector incomplete incorporation of expectations model, Palley (2003, 2011) drew similar conclusion on the threshold level of inflation. When inflation is low, inflation expectations are also low and are not incorporated into wage setting. As inflation increases, inflation expectations also rise and are increasingly incorporated into wage-setting leading to a steepening of the Phillips curve. After a threshold level, “…the Phillips curve bends back because workers start to ratchet up their incorporation of inflation expectations faster than the increase in inflation”. At some high level of inflation, the Phillips curve would become vertical. In the context of the backward-bending Phillips curve or the aggregate supply (AS) curve, we may note that it is likely to be only a theoretical curio that may never be observed in practice. This is because with a regular smooth downward sloping aggregate demand (AD) curve and a backward bending AS curve, there would be either two equilibrium points – one on the downward sloping part of AS and the other on the upward sloping part of AS curve – or only one equilibrium point – either on the downward sloping part of AS or on the upward sloping part of AS curve. In the first case of two equilibria, the one on downward sloping part would be unstable equilibrium and the other on the upward sloping part of AS curve would be the stable equilibrium. Hence, the first one on the downward sloping part of the AS curve would not be observed in practice. In the second case of only one equilibrium point, the one obtained on the downward sloping part of AS curve would lead to absurd policy implications of any cut or downward shift in AD. Since such absurd implications are not observed in practice, the case when the AD curve is flatter than the AS curve with both being downward sloping is practically ruled out. The studies that enthusiastically consider the backward bending Phillips curve arguments have invariably overlooked this serious limitation. Moreover, the literature on the Phillips curve mostly focusses on the inflation-output relationship in an economy in the short to medium term. In contrast, the concept of the threshold inflation, as discussed in the previous section, is the long-term (equilibrium) inflation rate that maximises the long-term steady-state growth rate of the economy. We, therefore, focus on the alternative strand of literature explaining the inflation-output growth relationship that developed in parallel to the Phillips curve literature. Table 1 provides the review with a theoretical perspective. | Table 1: Literature Review – Theoretical Perspective on Threshold Inflation | | Study | Variables Considered and Channel of Impact | Conclusion | | 1. Mundell (1963) | Inflation↑→ Real Wealth↓→ Saving↑→ Interest Rate↓→ Investment↑→ Growth↑ | Direct relationship between inflation and growth | | 2. Tobin (1965) | Inflation↑→ Portfolio reshuffle with Investment↑ and Cash↓→ Capital Stock↑→ Growth↑ during adjustment from one SSG to another | - Do - | | 3. Sidrauski (1967a & b) | Inflation↑→ Real Balances↓→ Saving used for maintaining current Consumption and hence Utility→ No effect on Capital Stock and SSG. In case Savings Rate is constant, Inflation↑→ Demand for Real Balances↓→ Capital Intensity↑ during adjustment from one SSG to another | Super-Neutrality of money or No impact of inflation on SSG. | | 4. Stockman (1981) | Inflation↑→ Real Balance↓→ Household Expenditures on consumption and capital↓→ Growth↓ | ‘Stockman Effect’ of inverse relationship between inflation and SSG. | | 5. Haslag (1995) | Inflation↑→ Real Deposit Rate↓→ Bank Deposit Growth↓→ Investment Growth↓→ Growth↓ | - Do - | | 6. Haslag (1997) | Introduction of Money in Neo-classical Growth Model: Nature of relationship between Money (M) and Capital Assets (K) determines the relationship between inflation and growth. | Inflation↑→ Growth↓ if M and K are complements; Inflation↑→ Growth↑ if M and K are substitutes; and SSG is Neutral to Inflation if M is only medium of exchange. | | 7. Greenwood & Huffman (1987); Cooley & Hansen (1989); Gomme (1993) | Inflation↑→ Relative Price of Leisure↓→ Demand for Leisure↑→ Supply of Labour↓→ Marginal Product of Capital↓→ Investment Rate↓→ Growth↓ | Inverse relationship between Inflation and Growth | | 8. Friedman (1977); Ball (1992); Pindyck (1991); Bernanke (1993); Bertola & Caballero (1994) | Inflation↑→ Uncertainty↑→ Effective Cost of Capital↑→ Investment Rate↓→ Growth↓ | Direct relationship between inflation and expected inflation uncertainty | | 9. Pourgerami & Maskus (1987); Ungar & Zilberfarb (1993) | Inflation↑→ Uncertainty of expected inflation↓ during high inflation phase | Inverse relationship between inflation and expected inflation uncertainty | | 10. Nasr et al. (2015); Barnett et al. (2018) | Survey of studies on the relationship between inflation and expected inflation uncertainty for different countries and datasets. | Strong support for a positive relationship during normal period, but negative relationship during crisis period. | | 11. Choi et al. (1996) | At high inflation level, Inflation↑→ Return on Saving↓→ Supply of Saving↓→Credit Rationing → Allocative Efficiency↓→ Growth↓. However, at low inflation level, credit rationing does not occur and Real Interest Rate↓→ Investment↑→ Growth↑ | Relationship between Inflation and Investment and Growth is non-monotonic | | 12. Li (2006); Cizkowicz & Rzonka (2013) | Empirical testing of relationship between inflation and investment | Non-linear relationship between inflation and investment | | 13. Akerlof et al. (1996); Danquah et al. (2011); Rondan & Chavez (2004) | Inflation↑→ Cost of Investment↑→ Reallocation of resources→ Efficiency gains or TFPG↑→ Growth↑ at low level of inflation. At high level of inflation, as Inflation↑→ Cost of Investment↑→ Allocative Efficiency loss or Investment Productivity↓→ Growth↓ | Non-monotonic relationship between inflation and growth | | 14. Dholakia (2020) | Inflation↑→ Inflation Uncertainty defined with structure of relative prices (IU)↑ eventually→ expected returns↓→ Growth of Capital Stock↓→ Growth↓. Simultaneously, Inflation↑→ TFPG or IOCR↑ because substantial structural changes occur in developing countries with low base inflation→ Growth↑. For developed countries, Inflation↑→ Cost of Investment↑→ TFPG↓→ Growth↓ | Non-monotonic or inverted-U shape relationship between inflation and investment rate; and between inflation and IOCR; and hence between inflation and growth. | | Source: Compiled by authors from various sources. | It is evident from Table 1 that the early literature emphasising unidirectional relationship between inflation and economic growth in the long run in either direction is not consistent as it would result in implausible and unrealistic outcomes. Later studies, however, argue convincingly for a non-monotonic – particularly an inverted-U shaped rather than U-shaped – relationship between inflation and growth. Thus, there would be a threshold level of inflation where growth would be maximized. The literature on empirical estimation corroborates the existence of a non-monotonic relationship between inflation and economic growth in the long run. Various cross-country studies provide a wide range of inflation thresholds across economies. The differences in estimates are mostly due to different datasets, concept and measurement of inflation, and the empirical strategy employed for estimation by those studies. 3.2 Empirical Literature in the International Context One of the earliest studies providing empirical analysis of inflation-growth trade-off is Sarel (1996), which uses data for about 90 countries for the period 1970-90 and examines the possibility of nonlinear effects of inflation on economic growth. The study finds significant structural break in the inflation and growth relationship when the inflation rate is 8 per cent. Below that rate, inflation does not have any effect on growth, or it may even have a slightly positive effect while the inflation rate of above 8 per cent adversely affects economic growth in a statistically significant manner. Ghosh and Phillips (1998) use panel regressions allowing for a nonlinear specification and find a statistically and economically significant negative relationship between inflation and growth, which holds true at all but the lowest inflation rates. According to them, when a linear model is fitted onto the data, raising inflation from 10 per cent to 20 per cent has a statistically significant impact of reducing growth but only by 0.01 percentage point. In contrast, when a nonlinear model is used, the impact is not only statistically significant but much higher at 0.3-0.4 percentage point reduction in growth. They find evidence of a 2.5 per cent inflation as threshold level – while acknowledging that 5 per cent or 10 per cent thresholds work almost as well statistically. The widely cited Khan and Senhadji (2001) study re-examined the issue of the existence of threshold level of inflation, using new econometric techniques that provide appropriate procedures for estimation and inference. The threshold level of inflation using CPI data was estimated at 1-3 per cent for industrial countries and 11-12 per cent for developing countries. Burdekin et al., (2004) and David et al., (2005) find much higher level of threshold inflation – the former find that inflation does not seem to significantly hurt growth until the range of 20-40 per cent for developing countries, while the latter find a threshold level of 19 per cent for developing and 12.6 per cent for industrial countries. They also conclude that the non-linearity in the inflation-growth relationship must always be accounted for and that a sample of industrial and developing countries should not be mixed. Vaona and Schiavo (2007) employ non-parametric and semi-parametric estimation techniques to find the existence of a non-linear relationship between inflation and growth using a sample of 85 countries (out of which 19 were developed countries) for the period 1960-1999. They estimate the threshold level of inflation at about 12 per cent for developed countries but find no clear relationship in the case of developing countries. There are also somewhat recent cross-country studies – Bick (2010), Espinoza et al., (2011), Jha and Dang (2012) and Kremer et al., (2013) – which have attempted estimation of threshold level of inflation. These studies mostly rely on threshold panel regressions estimated over a sample period from 1950 to 2010 and find threshold level of inflation in the range of 10-12 per cent for developed countries and 12-20 per cent for developing countries. In contrast, Omay and Kan (2010) find a statistically significant negative relationship between inflation and growth above an endogenously determined threshold level of inflation at 2.52 per cent for six industrialised countries. Das and Loxley (2015) investigate the inflation-growth relationship for 54 developing countries from Asia, Latin America and Sub-Saharan Africa and obtain threshold level in the range of 15-24 per cent. A wide range of threshold inflation estimates suggested by the literature points towards an important aspect that the estimate of threshold inflation is sensitive to the data frequency, sample size and time span of the study. In addition, regime and structural changes also make substantial difference to the estimates. Country-specific macroeconomic features, such as the level of financial development, capital accumulation, trade openness and fiscal expenditures also influence the non-linear inflation-growth relationship (Eggoh and Khan, 2014). On the other hand, the studies focusing on individual countries, especially those among developing economies, find much lower levels for threshold inflation. Chowdhury and Ham (2009) use a threshold VAR model and find 8.5-11.0 per cent range for threshold level of inflation for Indonesia. Based on the data from 1970 to 2005, Munir and Mansur (2009) find threshold inflation level of 4 per cent for Malaysian economy. In the case of Mexico, Risso et al. (2009) find that GDP growth and overall macro-economy was at risk of being jeopardized if inflation rate exceeds 9 per cent. Mubarik (2005) finds similar results for Pakistan’s economy. Vinayagathasan (2013) analyses several Asian economies over a period 1980-2009 and finds that inflation hurts growth when it exceeds 5.43 per cent but inflation lower than this level has no effect on growth. Thanh (2015) finds that inflation above the threshold level of 7.84 per cent starts to impede growth in ASEAN-51 countries. A threshold inflation of 7.97 per cent is observed for Turkish Republics2 by Aydin et al. (2016). Most of these studies use annual data on CPI as a measure of inflation. The use of annual data suggests the attempt to estimate a long-run relationship. Their results differ substantially because of the differences in sample of countries and time periods and the method of estimation. Generally, the threshold inflation level is found to be significantly higher for the developing economies than for the developed economies. Furthermore, when inflation rate is lower than the threshold level, its relationship with growth is found to be weak, while higher than threshold inflation could impact growth negatively though its magnitude may differ widely. Another striking feature of the existing empirical literature on the relationship between inflation and economic growth is the lack of a theoretical framework supporting the estimation strategy. As a result, it is natural that the estimates are likely to be subject to the specification error both in terms of omitted or unnecessarily included variables and functional form. Further, these studies between growth and inflation do not use the simultaneous equation framework and therefore their results suffer from the simultaneity bias (Chaturvedi et al., 2009). When the relationship in a simultaneous equation model is considered and the tests for causality direction between growth and inflation are conducted by Chaturvedi et al. (2009), they find the causality running only from inflation to growth and, that too, negatively for their sample of South-East and South Asian countries. Using only Indian data, however, Dholakia (2014) finds the bi-directional causality between growth and inflation. It is important to test the direction of causality and exogeneity to avoid errors and biases in the estimation of the threshold inflation. 3.3 Empirical Studies in the Indian Context In the Indian context, some of the early efforts at investigating the inflation-unemployment trade-off are Rangarajan (1983) and Dholakia (1990). Rangarajan analyses the relationship for the industrial sector and concludes that there was no trade-off between inflation and unemployment. Dholakia (1990) uses the extended Phillips curve framework for the whole economy and finds a horizontal aggregate supply curve thus denying that there exists a trade-off between inflation and growth in India. These studies were, however, based on the pre-liberalisation period when prices of many commodities were administered. More recent studies by Paul (2009) and Dholakia and Sapre (2012) find an upward sloping aggregate supply curve. Dholakia and Sapre (2012) incorporate the speed of adjustment in the extended Phillips curve framework and find a positive relationship between output and inflation. A number of studies also find evidence of a threshold level of inflation rate beyond which inflation has adverse impact on growth rate, implying a backward-bending dynamic aggregate supply curve. Some of the early studies suggesting threshold level of inflation in the Indian context are Chakravarty Committee (1985), which defined an annual inflation rate of 4 per cent as the tolerable level, and Rangarajan (1998) that viewed inflation rate at 6 per cent as “acceptable level”. The Chakravarty Committee referred to 4 per cent as the acceptable rise in prices reflecting changes in relative prices necessary to attract resources to growth sectors. Rangarajan (1998) advocates that monetary policy should be conducted in such a way that inflation rate remains below 6 per cent so that the value of money used as an input in the production process is not eroded, fiscal stability is maintained, and that there are no major social costs of inflation. Several subsequent studies use spline regression techniques and provide various estimates of threshold inflation (Table 2). | Table 2: Threshold Inflation Estimates for Indian Economy | | Study | Period | Inflation Threshold (%) | Methodology | Measure | Frequency | | Chakravarty Committee Report (1985) | | 4 | | WPI | | | Rangarajan (1998) | | 6 | | WPI | | | Kannan and Joshi (1998) | 1981-1996 | 6-7 | Spline regression | WPI | Annual | | Vasudevan, Bhoi and Dhal (1998) | 1961-1998 | 5-7 | Spline regression / Non-linear approach | WPI | Annual/ Monthly | | Report on Currency and Finance (2002) | 1971-2000 | 5 | Spline regression | WPI | | | Singh and Kalirajan (2003) | 1971-1998 | No Threshold (negative relation between growth and inflation) | Spline regression | WPI | Annual | | Bhanumurthy and Alex (2010) | 1976-2004/ 1997 Q1-2005 Q4/ Jan 2000-April 2007 | 4-4.5 | Non-linear least squares | WPI | Annual/ Quarterly/ Monthly | | Singh, Prakash (2010) | 1971-2009 | 6 | Spline regression / Non-linear least squares | WPI | Annual | | RBI Annual Report 2010-11 | | 4-6 | Spline regression / Non-linear least squares/ Logistic smooth transition regression | | | | Pattanaik and Nadhanael (2013) | 1972-2011 | 6 | Spline regression, Non-linear approach, VAR | WPI | Annual | | IMF (2012) | 1996-2012 | 5-6 | | | Quarterly | | Mohanty et al (2011) | 1996-2011 | 4-5.5 | Spline regression / Non-linear least squares/ Logistic smooth transition regression | WPI | Quarterly | | RBI (2014) | 1997-2013 | 6.2-6.7 (CPI-C)/ 4.6-5.8 (WPI) | Logistic smooth transition regression/ threshold VAR | WPI/CPI-C | Quarterly | | Mohaddes and Raissi (2014) | 1989-2013 | 5.5 | Cross-section augmented distributed lag approach, Panel ARDL | CPI-IW | Annual | | Behera and Mishra (2017) | 1990-2013 | 4 | Spline regression | WPI | Monthly | | Rangarajan (2020) | 1982-2009 | 6-7 | Non-linear approach/ Non-linear Least Squares/ Threshold autoregressive model | WPI | Annual | | Dholakia (2020) | 1996-2019 | 5.4-6 | Macro-theoretic model | CPI | Annual | | Source: Compiled by authors from various sources. | Table 2 shows that the studies in the Indian context have mostly used WPI as a measure of inflation. Moreover, some of the studies have surprisingly used quarterly and monthly data to analyse steady state growth and long run equilibrium inflation rates with a view to estimating the threshold inflation. Since the steady state growth and equilibrium inflation rates are essentially long run concepts, employing monthly or quarterly data for such analysis may not be appropriate as these data typically tend to give more weights to transitory developments. Ideally, threshold level of inflation as discussed in the previous section should be treated as a long-run concept which can be estimated more meaningfully by using annual data. Moreover, the empirical studies on estimation of threshold level of inflation in the Indian context are largely based on pure statistical exercises without any strong theoretical basis as was the case with most of the cross-country studies mentioned above. This limitation was effectively addressed by Dholakia (2020) by providing a theory of growth and threshold inflation. The Harrod growth model with open economy instead of a closed economy is used as a starting point which makes the natural or potential growth of the economy a variable unlike a constant in the original model. That in itself would ensure balance between the warranted growth and natural growth resulting in a stable steady state growth solution. Introduction of inflation rate as a determinant of the warranted growth through both its components – investment rate and incremental output capital ratio (IOCR) – ensures that the warranted growth rate remains at the maximum level that corresponds to the threshold inflation rate. Based on this theoretical framework, Dholakia (2020) argued that threshold inflation for any economy is not unique but depends on policy parameters like FD/GDP ratio and CAD/GDP ratio. Accordingly, they provided a whole range of estimates of threshold inflation rate in India consistent with alternative values of FD/GDP ratio and CAD/GDP ratio. In the present paper, we apply the framework of Dholakia (2020) by operationalizing their theory with a cross-country estimation of the model. 4. An Operational Model for Threshold Inflation Our starting point to develop an operational model for estimating the threshold inflation rate that would maximize the long-term growth rate of an economy is to consider the direction of causality between growth and inflation. Chaturvedi et al. (2009) find unidirectional causality going from inflation to growth in the case of countries from south-east and south Asia. While confirming this finding for India, Dholakia (2014b) finds weak support for the reverse causality also. However, Dholakia (2020) argue that in an inflation targeting framework of monetary policy, long run inflation becomes a policy parameter and may be treated only as an explanatory variable and the long-term growth as a dependent variable. The lead-lag correlation based on the cross-country panel data as reported in Table 3 also supports such a treatment of the two variables. The table reveals that growth leads to inflation with a lag of 2 years and effect remains over the next five-six years with weak correlations, but inflation leads to growth over a much longer period of eight-nine years and with much stronger correlations. This finding ensures that the practice of taking five-year moving averages of inflation and growth in the empirical literature would satisfactorily address the issue of direction of causality.3 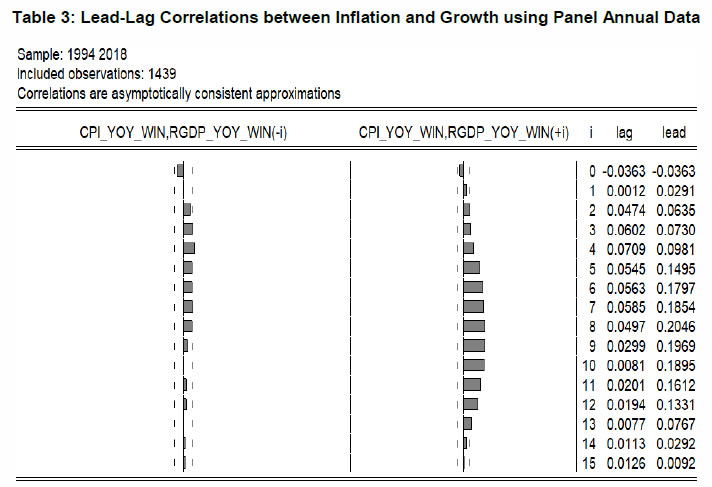 The next step is to consider the stable steady state growth solution in an open economy that Dholakia (2020) provide 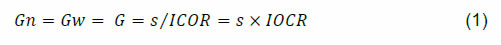 where Gn, Gw and G are respectively the natural, warranted and actual growth rates; s is the investment rate defined as a ratio of investment to GDP; IOCR is the incremental output capital ratio. This result assumes that the economy is at full employment long run equilibrium in the trade cycle context and hence saving equals investment. In order to get an operational model of threshold inflation, it is essential to relate both the components on the right-hand side of equation (1) to the rate of inflation in the economy. Our literature review clearly suggests that inflation is one of the determinants of both the investment rate (s) and the capital productivity (IOCR). However, a proper operationalization of the model requires considering other major determinants as well. The total investment in an economy could come from the government, foreign sources and domestic private investors or firms. This segregation would help us identify the other determinants of the total investment rate in an economy. Government or public investment forms a significant proportion of total investment in developing countries. The public investments are given by the capital outlay of the government, which is the difference between the fiscal deficit and the effective revenue deficit of the total government sector. The effective revenue deficit is the revenue deficit less the grants given to the sub-national units for creating capital assets. This relationship is very well supported empirically for India (Dholakia, 2020). Thus, the public investment rate depends on the fiscal policy of the government which is essentially captured by the fiscal deficit to GDP ratio net of effective revenue deficit. Similarly, private investment rate is a key component of overall investment rate and growth dynamics. In a model with government sector, an expansionary fiscal policy can have a ‘crowding in’ or ‘crowding out’ impact on private investment. An increase in public investment could increase private investment by improving infrastructural facilities or demand conditions that would improve profitability for the private sector. Mitra (2006) finds in the Indian context that government investment crowds out private investment in the short term, whereas it encourages private investment over the medium to long-term because it removes infrastructural bottlenecks and improves returns on private investments. Bahal and Raissi (2015) find evidence of crowding out of private investment in India for their full sample period 1950-2012 but find crowding in effect for the subsample period 1980-2012. They attribute this to the policy reforms which were initiated during the early 1980s and gained momentum after 1991. Private investment also depends upon real interest rate (r) through the financing cost channel and opportunity cost channel. Several studies find negative relationship between real interest rate and corporate investment (Tokuoka, 2012). IMF (2013) suggests that one fourth of the explained slowdown in investment in India during 1996 to 2012 could be attributed to high real interest rates. RBI (2013) shows that a 100 basis points increase in real lending rate lowers investment to GDP ratio by 9 bps in the short-run and 51 bps in the long-run. There is, however, a possibility that a decrease in real interest leads to lower investment through the supply of funds channel. According to McKinnon (1973), in a financially repressed economy, it is difficult for economic agents to find required resources from external sources to make investment due to non-price credit rationing. Also, physical capital is often indivisible. Hence, it becomes necessary for potential investors (savers) to accumulate savings for some time before they get enough resources for lump sum investments. As long as the rate of return on savings is less than the rate of return on physical capital, an increase in savings rate encourages accumulation of funds, which, in turn, increases the investment subsequently as suggested by McKinnon’s “complementarity hypothesis.” Therefore, an increase in real interest rate may lead to an increase in investment, albeit with a lag. There are also a number of studies that provide empirical evidence for a positive relationship between inflation and inflation uncertainty and its adverse influence on investment decisions of enterprises (Ferderer, 1993; Serven and Solimano, 1993, Pindyck and Solimano, 1993; Kalckreuth, 2000; Byrne and Davis, 2004; and Fisher, 2009). For India, Tokuoka (2012) finds that volatility of inflation has a negative and significant impact on corporate investment. The foreign investment rate may not be a major component of the total investment rate in a geographically large economy. The basic determinants of the foreign investment in any economy would be the real interest rate and Macroeconomic Vulnerability Index (MVI) suggested by GoI (2015), which is defined as the sum of the three policy parameters, namely inflation rate, fiscal deficit (FD) as a percentage of GDP and the current account deficit on balance of payments (CAD) as a percentage of GDP. As such, GoI (2015) argues that foreign investments are determined by what they define as the Rational Investors’ Rating Index (RIRI), which is the difference between real growth rate and one-third of MVI. If the growth rate of real GDP is taken as a proxy for the real interest rate, RIRI becomes a linear combination of all the four factors determining the foreign investment rate. Dholakia (2020) argue that there are logical arguments to expect the impact of all these variables on either direction of the foreign investment rate and that the rationale for their influence is also overlapping. The empirical evidence for India provided by them also supports their argument. Thus, considering all the three components of the investment rate and the ultimate factors determining each of them, we get the following equation Based on our discussion and the literature review, investment rate may be non-linearly related with inflation rate (π), while the other variables can have the linear relation. We may, therefore, consider higher order polynomials for π in the equation. The next component of our model is the equation for Capital Productivity or incremental output capital ratio (IOCR). It is important to note that IOCR used in the equation (1) above to define the real growth rate is the capital productivity over time when everything may change. Thus, it is a concept measured through the total differential of the aggregate production function rather than the partial derivative with respect to capital. As a result, total factor productivity growth (TFPG) can be shown to be an integral part of the IOCR4. A relatively high inflation naturally increases the cost of investment in the economy making firms respond to reallocate resources more efficiently (Danquah et al. 2011). Thus, higher inflation when the base is low corresponds to a higher TFPG (Rondan and Chavez, 2004). When inflation is relatively high, it entails high degree of uncertainty and makes the resource reallocation riskier and more inefficient leading to lower TFPG. Since capacity utilisation measures the extent to which an economy uses its installed production capacity, increase in capacity utilization would mean more efficient use of resources and hence higher TFPG. The output gap is used as a proxy to measure the capacity utilization (Michaelides and Milios, 2009). Higher fiscal deficit invariably leads to higher aggregate demand resulting in increased efficiency of resource use and increased TFPG when the output gap is negative. However, in the long run when full utilization of capacity is assumed, fiscal deficit by the government often results in creating public infrastructure or providing essential credit to the productive sectors thereby increasing the capital productivity in the system. Similarly, higher current account deficit (CAD) may imply higher foreign investment, which is associated with greater extent of the technology transfer (when FDI increases) and better management practices (when FII and debt flows in addition to FDI increase) leading to higher productivity growth. It is also possible that higher CAD may lead to the currency depreciation that may prove detrimental to capital productivity by increasing the cost of imported resources. Thus, considering the ultimate determinants of IOCR as discussed above, we get the following equation for IOCR – It may be noted that based on the literature review and our discussion above, the relationship between IOCR and π could be non-linear though with the other two variables it could be linear. Considering equations (1) to (3) together, we can express growth in general as –  Since growth (G) is a product of s and IOCR, its precise functional form depends on the functional forms of the two components, particularly with respect to inflation (π). If both the components are linear in π, the equation for growth would be a polynomial of degree two, which is the case considered by Dholakia (2020). However, if any one of the components has a polynomial of degree two or more in π, the equation for G would be a polynomial of the sum of the two degrees in π. Similarly, the interaction terms would also be accordingly more. This feature requires a dataset that would provide enough degrees of freedom to experiment with alternative functional forms. A study on any individual country will require a long time series of annual data if the results have to be statistically reliable. But a very long historical data series may not be relevant and reliable because significant regime shifts would generally occur on account of economic reforms being carried out over time. Therefore, the appropriate dataset for estimating such a relationship would be to consider cross-country panel data for relatively recent period. After estimating the above equation, the threshold level of inflation may be calculated using the first partial derivatives of this equation and first and second order conditions for maximisation. It is evident that there would not be a unique value of threshold inflation since it would depend on the values of other explanatory variables, particularly the policy targets for FD and CAD. This is one of the main contributions of this approach – it allows estimation of threshold level of inflation which is consistent with other macroeconomic policy parameters. The above discussion outlines the broad strategy for empirical estimation of the model and threshold inflation. One can further change the exact specifications and form of the equations to be estimated depending upon the availability of data and nature of information available. The model could also be fine-tuned in line with different settings across economies. With a view to having a more meaningful estimation, one may first like to find empirical support for individual equations of the model and then arrive at the final reduced form equation (Equation 4). We find a reasonably good empirical support for these equations using the panel data for 1995 to 2018 from a set of developed countries as well as developing countries. These results and estimation of threshold inflation are discussed in the next section. 5. Empirical Estimates Dholakia (2020) have used the above model to estimate threshold inflation for India using the data for the period 1995-96 to 2018-19. In this study, we deploy the proposed model to estimate threshold inflation in a cross-country panel data setting. We first estimate the model and then use the estimates to derive optimal combination of inflation and long-run growth in the international perspective. The benefit of using cross-country panel data is a considerably large number of observations that would allow to estimate higher-order polynomial of the reduced-form equation for long-run growth with adequate degrees of freedom. Similarly, this also makes it possible to study the non-linear relationship between inflation and long-run growth simultaneously for developed and developing countries. Our country-wise panel dataset is compiled from the World Economic Outlook database of the International Monetary Fund (IMF). The dataset consists of, inter alia, annual time-series data on gross domestic product (GDP), total investment (as per cent of GDP), current account balance (as per cent of GDP), fiscal balance (as per cent of GDP) and consumer price index-based inflation for 194 countries from 1980 to 2018. Data on crude oil prices (WTI Brent Crude) and terms of trade were extracted from Bloomberg and IMF’s commodity terms of trade database. We rank all the countries on the basis of their share in annual World GDP in 20175 and select the top 65 countries that together represent 95 per cent of the total World GDP. Out of these, we further select the countries having continuous data on all four variables for our entire sample period from 1995 to 2018. This leaves us with a panel dataset of 58 countries in total which includes 26 advanced economies (AEs) and 32 emerging market economies (EMEs). In order to smooth out plausible short- and medium-term business cycle fluctuations, we treat all variables by computing a five year-moving average for each of them. Additionally, since some of the countries in our sample (such as Brazil, Russia, Poland and Turkey) experienced bouts of very high inflation, especially during the early 1990s, the data is winsorized in order to limit the effect of outliers on our econometric exercise described next. The final data set used for estimation showed average growth rate of 3.5 per cent for full sample with a standard deviation of 3.6 per cent. The inflation rate, on the other hand, showed larger variation with standard deviation of 15.1 per cent and an average of 8.3 per cent. The variations in growth and inflation rates were larger in the case of emerging market economies compared with advanced economies. Advanced economies in the sample, on an average, showed surplus in the current account while the current account of emerging market economies was in deficit. It may be noted that the overall current account is negative and not in balance. This is because the average has been computed for each country on the basis of ratios of respective country’s GDP which need not to be zero. Another reason is because many smaller countries are not part of the sample. Gross fiscal deficit showed more or less similar pattern across advanced and emerging market economies, partly reflecting the impact of winsorization (Table 4). | Table 4: Summary Statistics for the Final Panel Data Sample used in the Study | | Country Sample/ Statistics | GDP Growth
(%) | Inflation Rate
(%) | CAD
(% of GDP) | Fiscal Deficit
(% of GDP) | | Full Sample | | Mean | 3.5 | 8.3 | -0.7 | 2.1 | | Median | 3.4 | 3.5 | 0.3 | 2.4 | | Min | -7.3 | -1.2 | -23.8 | -11.6 | | Max | 12.7 | 80.9 | 24.3 | 13.5 | | Std. Dev | 3.6 | 15.1 | 6.1 | 4.2 | | Advanced Economies | | Mean | 2.6 | 2.4 | -1.9 | 2.0 | | Median | 2.5 | 2.0 | -1.3 | 2.3 | | Min | -7.3 | -1.2 | -23.8 | -11.6 | | Max | 12.7 | 20.3 | 14.5 | 13.5 | | Std. Dev | 2.8 | 2.5 | 5.8 | 4.2 | | Emerging Market Economies | | Mean | 4.3 | 13.1 | 0.3 | 2.2 | | Median | 4.7 | 6.8 | 1.2 | 2.5 | | Min | -7.3 | -1.2 | -23.8 | -11.6 | | Max | 12.7 | 80.9 | 24.3 | 13.5 | | Std. Dev | 4.0 | 19.0 | 6.1 | 4.2 | Considering the full sample at hand, we begin by separately estimating the equation for investment rate as a function of its own lagged value, inflation, current account deficit and fiscal deficit (equation 2). Since inflation is our primary variable of interest, we consider both linear and quadratic forms of relationship between investment rate and inflation. Using measures for goodness of fit (adj-R2) and Bayesian information criterion (BIC) for model selection, we find that a quadratic form of relationship between investment and rate of inflation provides the best fit (Table A1). We repeat the same exercise for IOCR – the other main determinant of long-run growth in our model apart from rate of investment – and find that a linear form of relationship between IOCR and inflation provides the best fit (Table A2). Combining these results would give a cubic form of relationship in the reduced form equation of growth on inflation. Speaking mathematically, this implies that there is a possibility of finding a growth-maximizing rate of inflation (the local maxima) and a growth-minimizing inflation rate (the local minima) – a possibility that Dholakia (2020) ignored since they considered only a quadratic function. Although our interest lies in finding the growth-maximizing rate of inflation, it would be interesting to get an idea about the growth-minimizing rate of inflation and the corresponding growth rate. Fiscal deficit and current account deficit are other determinants of long-run growth. Therefore, the final model can be depicted as shown below:  The full and sub-sample regression estimates have been provided in Table 5. Panel (A) represents our baseline model estimated for the full sample where long-run growth is assumed to depend non-linearly on inflation, fiscal deficit and current account deficit. In panel (B) and (C) of Table 4, the same model has been estimated for Advanced Economies (AEs) and Developing or Emerging Market Economies (EMEs) separately. The estimations suggest a satisfactory goodness of fit considering that there is a large number of observations with all variables being proportions measured as percentages with the heterogeneities in the dataset. Redundant variable and Wald tests confirmed that the higher polynomials of order 2 and 3 of inflation rate were significant at 10 per cent level of significance (Table A4). | Table 5: Growth Regressions - Results | | Explanatory variable | Full Sample (A)
GDPg | AEs (B)
GDPg | EMEs (C)
GDPg | | Inf^3(-1) | 0.0000257
(0.0000208) | 0.000219
(0.00301) | 0.0000123
(0.0000240) | | Inf^2(-1) | -0.00336*
(0.00192) | -0.0401
(0.0402) | -0.00214
(0.00223) | | Inf(-1) | 0.116**
(0.0473) | 0.372
(0.228) | 0.117**
(0.0457) | | CAD^2(-1) | 0.00436**
(0.00181) | -0.000367
(0.00324) | 0.0129***
(0.00260) | | FD^2(-1) | -0.00234
(0.00525) | -0.0114*
(0.00619) | 0.00185
(0.0133) | | FD(-1)*Inf^2(-1) | -0.000158
(0.000169) | 0.00422
(0.00463) | -0.000239
(0.000152) | | FD(-1)*Inf(-1) | -0.00431
(0.00742) | -0.0140
(0.0418) | 0.00800
(0.00805) | | CAD(-1)*Inf^2(-1) | 0.0000809
(0.0000787) | -0.0183**
(0.00695) | 0.000149*
(0.0000748) | | CAD(-1)*Inf(-1) | -0.00400
(0.00600) | 0.0642*
(0.0365) | -0.0122**
(0.00514) | | FD(-1)*CAD(-1) | -0.0182***
(0.00483) | -0.00867
(0.00781) | -0.0347***
(0.00753) | | FD(-1) | -0.163**
(0.0765) | -0.0253
(0.0671) | -0.421***
(0.0699) | | CAD(-1) | -0.0297
(0.0441) | -0.177***
(0.0583) | 0.183***
(0.0364) | | Constant | 3.474***
(0.309) | 2.144***
(0.475) | 4.357***
(0.218) | | adj. R2 | 0.3205 | 0.5504 | 0.4419 | | N | 1218 | 586 | 632 | Note: Standard errors in parentheses; * p < 0.10, ** p < 0.05, *** p < 0.01; Country FE = Yes; Time FE = Yes.
Source: Authors’ estimates. | Based on these regressions estimates, the optimum values of steady state growth rate and threshold inflation rate, for alternative values of the fiscal deficit and current account deficit, are provided in Table 6. If we consider a fixed value for fiscal deficit (FD/GDP) at 6.0 per cent and for current account deficit (CAD/GDP) at 2.0 per cent of GDP, our model predicts a threshold inflation rate of 11.0 per cent for the full sample, 4.1 per cent for advanced economies but a much higher threshold rate of inflation at 24.8 per cent for emerging economies. It may be noted that in our empirical strategy, we have used lagged values to address the issue of endogeneity inherent in a regression involving growth, inflation, FD, and CAD. As a further robustness check, we employ a dynamic panel generalized method of moments (GMM) for estimation of the above equation. The GMM results are broadly in line with the OLS estimates. For the full sample, threshold inflation varies from 6.3 per cent to 13.8 per cent, and the optimal growth rate lies in a range of 4.8 per cent to 6.0 per cent for different values of FD and CAD. (Table A5 and A6). | Table 6: Threshold inflation and Optimal Growth Estimates | | (per cent) | FD
(as % of GDP) | CAD
(as % of GDP) | Full Sample | Advanced Economies | EMEs | | Threshold inflation | Growth rate | Threshold inflation | Growth rate | Threshold inflation | Growth rate | | 3.00 | 2.00 | 15.40 | 3.64 | 3.65 | 2.24 | 28.55 | 5.23 | | 3.00 | 2.50 | 15.25 | 3.59 | 3.40 | 2.14 | 27.90 | 5.19 | | 6.00 | 2.00 | 11.00 | 2.73 | 4.16 | 1.84 | 24.86 | 3.94 | | 6.00 | 2.50 | 10.83 | 2.66 | 3.78 | 1.70 | 24.33 | 3.86 | | 6.50 | 2.00 | 10.43 | 2.59 | 4.28 | 1.75 | 24.47 | 3.74 | | 6.50 | 2.50 | 10.26 | 2.51 | 3.86 | 1.61 | 23.96 | 3.64 | | 7.00 | 2.00 | 9.89 | 2.44 | 4.40 | 1.66 | 24.11 | 3.53 | | 7.00 | 2.50 | 9.72 | 2.36 | 3.95 | 1.52 | 23.62 | 3.43 | | Source: Authors’ estimates. | Our model can be flexibly extended to generate country-specific estimates through appropriate adjustments. To show this, we include a binary independent variable for India in our baseline regression model for growth. We also introduce a slope dummy variable by interacting a binary variable with inflation to obtain India-specific estimates. This model specification essentially adjusts the average mean growth rate and slope of equation with respect to inflation for the sample to derive India-specific estimates6 presented below in Table 7. For macroeconomic policy targets consistent with maintaining fiscal deficit at 6.0 per cent and current account deficit at 2.0 per cent of GDP, our estimates suggest a threshold inflation level of 6.1 per cent and optimal growth rate of 7.5 per cent for India. Chart 1 provides the estimated growth - inflation scenarios in India given the alternative combinations of the other policy targets – fiscal deficit and current account deficit as proportion of GDP.7 The chart shows that the local maximum and minimum values of growth rate with respect to inflation rate in India are very close. The growth is maximized around 6 per cent of long-term inflation rate and is minimized around 9.5 per cent of inflation. If we consider the inflation target at 4 per cent instead of the threshold level of 6 per cent, the long-term growth rate would decline by about 80 bps. On the other hand, if we consider the inflation target of 8 per cent instead of the threshold level of 6 per cent, the long-term growth rate would decline by only about 30 bps. Thus, the trade-off between long-term inflation and growth is not symmetric on both side of the threshold inflation. When the inflation target is less than the threshold level, the sacrifice is 0.4 per cent point growth per one per cent point reduction in long-term inflation. However, if the inflation target exceeds the threshold level, the sacrifice of growth is only 0.15 per cent point per one per cent point increase in the long-term inflation. | Table 7: India-specific Threshold inflation and Optimal Growth Estimates | FD
(as % of GDP) | CAD
(as % of GDP) | Threshold Inflation
(per cent) | Growth Rate
(per cent) | | 5.0 | 2.0 | 6.15 | 7.74 | | 5.0 | 2.5 | 6.15 | 7.68 | | 6.0 | 2.0 | 6.13 | 7.48 | | 6.0 | 2.5 | 6.12 | 7.41 | | 7.0 | 2.0 | 6.10 | 7.22 | | 7.0 | 2.5 | 6.10 | 7.14 | | 8.0 | 2.0 | 6.08 | 6.96 | | 8.0 | 2.5 | 6.08 | 6.87 | | Source: Authors’ estimates. |
Since the estimates generated from any model could be sensitive to model specification and sampling, we subject our model to sensitivity checks based on inclusion of other exogenous variables and sampling (Table A3). Table 8 shows the threshold inflation and growth estimates after adding terms of trade (ToT) as an additional independent variable in our growth regression model8. Similarly, Table 9 shows the estimates based on model estimated for panel of countries that are net importers of crude oil9. Note that derived estimates for threshold inflation and optimal growth are very similar to those presented earlier. | Table 8: Threshold inflation and Optimal Growth Estimates with Terms of Trade | | (per cent) | FD
(as % of GDP) | CAD
(as % of GDP) | Full Sample | EMEs | | Threshold inflation | Growth rate | Threshold inflation | Growth rate | | 3.0 | 2.0 | 18.35 | 3.55 | 31.60 | 5.10 | | 3.0 | 2.5 | 17.99 | 3.49 | 30.50 | 5.00 | | 6.0 | 2.0 | 11.66 | 2.44 | 26.64 | 3.50 | | 6.0 | 2.5 | 11.36 | 2.36 | 25.62 | 3.38 | | 6.5 | 2.0 | 10.65 | 2.26 | 25.94 | 3.24 | | 6.5 | 2.5 | 10.35 | 2.18 | 24.94 | 3.11 | | 7.0 | 2.0 | 9.65 | 2.09 | 25.28 | 2.97 | | 7.0 | 2.5 | 9.36 | 2.00 | 24.29 | 2.84 | | Source: Authors’ estimates. |
| Table 9: Threshold inflation and Optimal Growth Estimate for Oil Importing Nations | FD
(as % of GDP) | CAD
(as % of GDP) | Oil importing countries | | Threshold inflation (%) | Growth rate (%) | | 3.0 | 2.0 | 15.91 | 5.20 | | 3.0 | 2.5 | 16.63 | 5.24 | | 6.0 | 2.0 | 13.49 | 4.17 | | 6.0 | 2.5 | 14.25 | 4.18 | | 6.5 | 2.0 | 13.06 | 3.99 | | 6.5 | 2.5 | 13.83 | 3.99 | | 7.0 | 2.0 | 12.61 | 3.81 | | 7.0 | 2.5 | 13.39 | 3.81 | | Source: Authors’ estimates. | 6. Consistency of Target Quartet and Concluding Remarks The study draws upon literature on economic growth which suggests that growth depends on investment rate and productivity of capital. Inflation rate influences investment rate through the uncertainty channel. Apart from the inflation rate, fiscal and current account deficit are other major determinants of investment. Similarly, capital productivity is also influenced by inflation that allows flexibility in relative prices for the necessary structural changes in the economy. Thus, the proposed framework entails a non-linear relationship between long-term economic growth and long run equilibrium inflation. The major aim of this study was to consider a proper functional form for estimating a threshold level of inflation consistent with theoretical foundations. International panel data provide enough degrees of freedom to experiment with alternative functional forms. The empirical evidence suggests that the appropriate functional form for the long-term growth is a polynomial of third degree in π, and second degree in FD/GDP and CAD/GDP. The long-term growth-maximizing level of equilibrium inflation rate is the threshold inflation for an economy. A cubic function also provides the opposite of threshold inflation, i.e., the growth-minimizing inflation rate. Empirical exercise carried out in the present paper suggests that the growth-maximizing inflation rate is lower than the growth-minimizing inflation rate given the values of FD/GDP and CAD/GDP. It is not theoretically correct to say, therefore, that any higher rate of inflation than the threshold level is always inimical to growth10. On the other hand, it is correct to say that inflation rate lower than the threshold rate is always harmful to growth. Therefore, it is extremely important for the policy makers to identify the threshold level of inflation in the economy. It is also clear from the discussion of the concept and the empirical exercise carried out in the present paper that the threshold inflation is not unique in an economy, but always varies with the values of FD/GDP and CAD/GDP. Thus, setting internally consistent targets for FD/GDP, CAD/GDP, inflation rate and real growth rate is crucial for efficient macroeconomic management. If targets for this quartet are fixed independently of each other, they can result in substantial avoidable cost to the system, not only because the system would not be able to achieve all the targets, but also because the system would remain in disequilibrium requiring unnecessary policy interventions or adjustment costs. This, however, does not imply that the policy makers have to set the inflation target at the threshold level given the targets for the CAD/GDP and FD/GDP. If the threshold inflation rate is somehow considered to be too high, the policy makers can choose a lower inflation target only by consciously sacrificing long-term real growth of GDP. The present paper has provided clear theoretical and empirical evidence that inflation – growth trade-off exists even in the long run. Those who firmly believe in lack of any trade-off between inflation and growth (employment) in the long run and frame policies and targets accordingly are prone to ignore huge social costs of such policies. This point can be illustrated with the Indian case. Dholakia and Kadiyala (2017) estimate that the cumulative sacrifice of 3 to 4 per cent of GDP is involved to bring down equilibrium inflation rate by one percentage point. Exercise undertaken in the present study suggests that the long-term growth would fall by 40 basis points (or 0.4 percentage point) if the initial inflation rate was less than the threshold rate. However, if the initial inflation rate was higher than the threshold rate, it would result in an increase of long-term growth by 15 basis points. Even in the latter case, it would take more than two decades to recover the cost of sacrificing GDP to bring down the equilibrium rate of inflation. In the former case, the cost only compounds. Of course, there are arguments in favour of lower inflation rate in terms of its favourable redistribution impact particularly on the poor and the financial stability concerns. However, the findings of the present study caution the policy makers not to ignore the probable cost of lower inflation in terms of lower long-term growth of output and employment and hence lower rate of the poverty reduction. These costs and benefits of fixing a long-term inflation target will have to be considered while making the choice. Financial stability concerns can be considered only by modifying and extending the theory of growth and threshold inflation proposed by Dholakia (2020), which we have not addressed in the present paper. Finally, the present study, using international panel data from 1995-2019, complements and corroborates the findings of Dholakia (2020) in case of India. As it was pointed out earlier (in footnote 10), precise results may differ when a country-specific time-series data are used from the results obtained by using international panel data, and the former is recommended for the purpose of country-specific policy. However, the results of the present study, based on a different method and framework, that the threshold level of inflation (at given values of FD/GDP and CAD/GDP) is higher for emerging economies than for advance economies is in line with extant literature on the subject. Similarly, the findings here clearly show that the threshold inflation and corresponding growth are not unique for a country but depend on the other two parameters – FD/GDP and CAD/GDP. If a country chooses the target values of FD/GDP and CAD/GDP to be achieved in the long run, its potential output growth gets determined through the corresponding value of threshold inflation. If the country then chooses an inflation target that is lower than the threshold level, it cannot achieve its potential output growth and the system would remain in long-run disequilibrium requiring constant policy interventions to stabilize.
7. References Akerlof, G. A., Dickens, W. T., Perry, G. L., Bewley, T. F., & Blinder, A. S. (2000). Near-rational wage and price setting and the long-run Phillips curve. Brookings papers on economic activity, 2000(1), 1-60. Akerlof, G. A., Dickens, W. T., Perry, G. L., Gordon, R. J., & Mankiw, N. G. (1996). The macroeconomics of low inflation. Brookings papers on economic activity, 1996(1), 1-7 Aydın, C., Esen, Ö., & Bayrak, M. (2016). Inflation and economic growth: a dynamic panel threshold analysis for Turkish Republics in transition process. Procedia-Social and Behavioral Sciences, 229, 196-205. Bahal, R., & Raissi, M. T. (2015). Crowding-Out or Crowding-In? Public and Private Investment in India. Working Paper WP/15/264, International Monetary Fund, Washington D.C., USA. Bailey, M. J. (1956). The welfare cost of inflationary finance. Journal of political Economy, 64(2), 93-110. Ball, L. (1992). Why does high inflation raise inflation uncertainty? Journal of Monetary Economics, 29(3), 371-388. Barnett, W., Ftiti, Z., & Jawadi, F. (2018). The Causal Relationships between Inflation and Inflation Uncertainty (No. 86478). University Library of Munich, Germany. Behera, J., & Mishra, A. K. (2017). The recent inflation crisis and long-run economic growth in India: An empirical survey of threshold level of inflation. South Asian Journal of Macroeconomics and Public Finance, 6(1), 105-132. Bernanke, B. S. (1993). Credit in the Macroeconomy. Quarterly Review-Federal Reserve Bank of New York, 18, 50-50. Bertola, G., & Caballero, R. J. (1994). Irreversibility and aggregate investment. The Review of Economic Studies, 61(2), 223-246. Bhanumurthy, N. R., & Alex, D. (2008). Threshold Level of inflation for India (No. Institute of Economic Growth Discussion Paper Series No. 124/2008). New Delhi: University Enclave. Bick, A. (2010). Threshold effects of inflation on economic growth in developing countries. Economics Letters, 108(2), 126-129. Briault, C. (1995). The costs of inflation. Bank of England Quarterly Bulletin, 35(1), 33-45. Burdekin, R. C., Denzau, A. T., Keil, M. W., Sitthiyot, T., & Willett, T. D. (2004). When does inflation hurt economic growth? Different nonlinearities for different economies. Journal of Macroeconomics, 26(3), 519-532. Byrne J. P., Davis E. P., 2004. Permanent and Temporary Inflation Uncertainty and Investment in the United States. Economics Letters 85(2): 271-277. Chari, V. V., Christiano, L. J., & Kehoe, P. J. (1996). Optimality of the Friedman rule in economies with distorting taxes. Journal of Monetary Economics, 37(2), 203-223. Chaturvedi, V., Kumar, B., & Dholakia, R. H. (2009). Inter-Relationship between Economic Growth, Savings and Inflation in Asia. Journal of International Economic Studies, 23, 1-22. Choi, S., Smith, B. D., & Boyd, J. H. (1996). Inflation, Financial Markets, and Capital Formation. Federal Reserve Bank of St. Louis Review, 78, 9-35. Chowdhury, A., & Ham, R. (2009). Inflation targeting in Indonesia: Searching for a threshold. The Singapore Economic Review, 54(04), 645-655. Ciżkowicz, P., & Rzońca, A. (2013). Does inflation harm corporate investment? Empirical evidence from OECD countries. Economics: The Open-Access, Open-Assessment E-Journal, 7(2013-16), 1-38. Cooley, T. F., & Hansen, G. D. (1989). The inflation tax in a real business cycle model. The American Economic Review, 733-748. Danquah, M., Moral-Benito, E., & Ouattara, B. (2011). TFP growth and its determinants: nonparametrics and model averaging. Banco de Espana Working Paper No. 1104. Das, A., & Loxley, J. (2015). Non-linear relationship between inflation and growth in developing countries. Economic & Political Weekly, 50(37), 59-64. David, D., Pedro, G. P., & Paula, H. E. (2005). Threshold effects in the relationship between inflation and growth: a new panel-data approach (No. 38225). University Library of Munich, Germany. Dholakia, R H (1990). Extended Phillips Curve for the Indian Economy. Indian Economic Journal, 38 (1), pp 69-78. Dholakia, R. H. (2014 a). Sacrifice Ratio and Cost of Inflation for the Indian Economy. Indian Institute of Management Ahmedabad, Research and Publication Department.(No. WP2014-02-04). Dholakia, R. H. (2014 b). Cost and Benefit of Disinflation Policy in India. Economic and Political Weekly, 49(28), July 12; pp.165-169. Dholakia, R. H., & Sapre, A. A. (2012). Speed of Adjustment and Inflation–Unemployment Trade-off in Developing Countries–Case of India. Journal of Quantitative Economics, 10(1), pp. 1-16. Dholakia, R.H. and Kadiyala, V.S. (2017). How Costly is the Deliberate Disinflation in India? – Estimating the Sacrifice Ratio. Journal of Quantitative Economics, 15(1), pp. 27-44. Dholakia, R. H. (2020). “A Theory of Growth and Threshold Inflation with Estimates”, (Presidential Address by Ravindra H. Dholakia to the annual conference of The Indian Econometric Society, Madurai on Jan.8, 2020), Journal of Quantitative Economics, 18(3), Sept. 2020, pp.471-493. Driscoll, J. C., & Kraay, A. C. (1998). Consistent covariance matrix estimation with spatially dependent panel data. Review of economics and statistics, 80(4), 549-560. Eggoh, J. C., & Khan, M. (2014). On the nonlinear relationship between inflation and economic growth. Research in Economics, 68(2), 133-143. Espinoza, R., Leon, H., & Prasad, A. (2011). When should we worry about inflation?. The world bank economic review, 26(1), 100-127. Ferderer J. P., 1993. The Impact of Uncertainty on Aggregate Investment Spending: An Empirical Analysis. Journal of Money, Credit and Banking 25(1): 30-48. Fisher G., 2009. Investment Choice and Inflation Uncertainty, London School of Economics, mimeo. Friedman, M. (1968). The Role of Monetary Policy,'; American Economic Review, 58. repr. in M. Friedman (1969), 102-110. Friedman, M. (1969). The optimum quantity of money, and other essays (No. HG538 F866). Friedman, M. (1977). Nobel lecture: inflation and unemployment. Journal of political economy, 85(3), 451-472. Ghosh, A., & Phillips, S. (1998). Warning: Inflation may be harmful to your growth. Staff Papers, 45(4), 672-710. GoI (2015). Economic Survey 2014-15, Ministry of Finance, New Delhi, July. GoI (2019): Economic Survey 2018-19, Ministry of Finance, New Delhi, July. Gomme, P. (1993). Money and growth revisited: Measuring the costs of inflation in an endogenous growth model. Journal of Monetary economics, 32(1), 51-77. Greenwood, J., & Huffman, G. W. (1987). A dynamic equilibrium model of inflation and unemployment. Journal of Monetary Economics, 19(2), 203-228. Harrod, R. F. (1948). Towards a Dynamic Economics: Some recent developments of economic theory and their application to policy. MacMillan and Company, London. Haslag, J. (1995). Inflation and intermediation in a model with endogenous growth (No. 9502). Federal Reserve Bank of Dallas. Haslag, J. H. (1997). Output, growth, welfare, and inflation: a survey. Economic Review-Federal Reserve Bank of Dallas, 11-21. Hoechle, D. (2007). Robust standard errors for panel regressions with cross-sectional dependence. The stata journal, 7(3), 281-312. IMF. (2013). IMF Country Report No. 13/37: India Article IV Consultation. International Monetary Fund, Washington D.C., USA. Jha, R., & Dang, T. N. (2012). Inflation variability and the relationship between inflation and growth. Macroeconomics and Finance in Emerging Market Economies, 5(1), 3-17. Kalckreuth von U., 2000. Exploring the Role of Uncertainty for Corporate Investment Decisions in Germany, Deutsche Bundesbank Research Centre Discussion Paper Series. Economic Studies 05. Kannan, R., & Joshi, H. (1998). Growth-inflation trade-off: Empirical estimation of threshold rate of inflation for India. Economic and Political Weekly, 2724-2728. Khan, M. S., & Senhadji, A. S. (2001). Threshold effects in the relationship between inflation and growth. IMF Staff papers, 48(1), 1-21. Kremer, S., Bick, A., & Nautz, D. (2013). Inflation and growth: new evidence from a dynamic panel threshold analysis. Empirical Economics, 44(2), 861-878. Li, M. (2006). Inflation and economic growth: Threshold effects and transmission mechanisms. Department of Economics, University of Alberta, 2(5), 8-14. Lucas Jr., R. E. (1972). Expectations and the Neutrality of Money. Journal of economic theory, 4(2), 103-124. Michaelides, P., & Milios, J. (2009). TFP change, output gap and inflation in the Russian Federation (1994–2006). Journal of economics and business, 61(4), 339-352. Mitra, P. (2006). Has government investment crowded out private investment in India?. American Economic Review, 96(2), 337-341. Mohaddes, M. K., & Raissi, M. M. (2014). Does Inflation Slow Long-Run Growth in India? (No. 14-222). International Monetary Fund. Mohanty, D., Chakraborty, A. B., Das, A., & John, J. (2011). Inflation Threshold in India: An Empirical Investigation. Reserve Bank of India Working Paper Series, (18/2011). Mubarik, Yasir A., (2005). Inflation and Growth: An Estimate of the Threshold Level of Inflation in Pakistan. SBP-Research Bulletin, 1(1), 35- 44. Mundell, R. (1963). Inflation and real interest. Journal of Political Economy, 71(3), 280-283. Munir, Q., & Mansur, K. (2009). Non-linearity between inflation rate and GDP growth in Malaysia. Economics bulletin, 29(3), 1555-1569. Nasr, A. B., Balcilar, M., Ajmi, A. N., Aye, G. C., Gupta, R., & Van Eyden, R. (2015). Causality between inflation and inflation uncertainty in South Africa: Evidence from a Markov-switching vector autoregressive model. Emerging Markets Review, 24, 46-68. Omay, T., & Kan, E. Ö. (2010). Re-examining the threshold effects in the inflation–growth nexus with cross-sectionally dependent non-linear panel: Evidence from six industrialized economies. Economic Modelling, 27(5), 996-1005. Palley, T. I. (1994). Escalators and elevators: a Phillips curve for Keynesians. The Scandinavian Journal of Economics, 96(1), 111-116. Palley, T. I. (1997). Expected aggregate demand, the production period and the Keynesian theory of aggregate supply. The Manchester School, 65(3), 295-309. Palley, T. I. (2003). The backward–bending Phillips Curve and the minimum unemployment rate of inflation: Wage adjustment with opportunistic firms. The Manchester School, 71(1), 35-50. Palley, T. I. (2011). Monetary Union Stability: The Economics of the Phillips Curve: Formation of Inflation Expectations versus Incorporation of Inflation Expectations (No. 4-2011). IMK at the Hans Boeckler Foundation, Macroeconomic Policy Institute. Pattanaik, S., & Nadhanael, G. V. (2013). Why persistent high inflation impedes growth? An empirical assessment of threshold level of inflation for India. Macroeconomics and Finance in Emerging Market Economies, 6(2), 204-220. Paul, B P (2009). In Search of the Phillips Curve for India. Journal of Asian Economics, 20, pp 479-88. Phelps, E. S. (1967). Phillips curves, expectations of inflation and optimal unemployment over time. Economica, 254-281. Phelps, E. S. (1968). Money-wage dynamics and labor-market equilibrium. Journal of political economy, 76(4, Part 2), 678-711. Phelps, E. S. (1973). Inflation in the theory of public finance. The Swedish Journal of Economics, 67-82. Phillips, A. W. (1958). The relation between unemployment and the Rate of change of money wage rates in the United Kingdom, 1861–1957 1. Economica, 25(100), 283-299. Pindyck R. S., Solimano A., 1993. Economic Instability and Aggregate Investment. NBER Working Papers 4380. Pindyck, Robert S. (1991). Irreversibility, Uncertainty, and Investment. Journal of Economic Literature, 29 (3), 1110-1148. Pourgerami, A., & Maskus, K. E. (1987). The effects of inflation on the predictability of price changes in Latin America: some estimates and policy implications. World Development, 15(2), 287-290. Rangarajan, C (1983): “Conflict between Employment and Inflation” in A Robinson et al (ed.), Employment Policy in a Developing Country: A Case Study of India (London: Macmillan). Rangarajan, C. (1998), ';Development, Inflation and Monetary Policy';, in I. Ahluwalia, & I. Little, India's Economic Reforms and Development: Essays for Manmohan Singh. New Delhi: OUP. Rangarajan, C. (2020). The New Monetary Policy Framework-What it Means. Journal of Quantitative Economics, Vol. 18, No.2, May 2020, pp. 457-470. RBI (2002): Report on Currency and Finance, 2001-02, Reserve Bank of India, Mumbai. RBI (2002): Report on Currency and Finance, 2001-02, Reserve Bank of India, Mumbai. RBI (2011): Annual Report, 2010-11, Reserve Bank of India, Mumbai. RBI. (1985). Report of the Committee to Review the Working of the Monetary System (Chairman: Sukhamoy Chakravarty), Reserve Bank of India. RBI. (2013). Real Interest Rate impact on Investment and Growth–What the Empirical Evidence for India Suggests? RBI Project Research Study, Reserve Bank of India, Mumbai, India. RBI. (2014). Report of the Expert Committee to Revise and Strengthen the Monetary Policy Framework (Chairman: Urjit R. Patel), Reserve Bank of India. Risso, W. A., & Carrera, E. J. S. (2009). Inflation and Mexican economic growth: long-run relation and threshold effects. Journal of Financial Economic Policy, 1(3), 246.Ronald I. McKinnon. (1973). Money and capital in economic development. Brookings Institution Press. Rondan, N. R. R., & Chavez, J. C. A. (2004). High inflation, volatility and total factor productivity. Banco Central De Reserva Del Peru, (5), 1-18. Samuelson, P. A., & Solow, R. M. (1960). Analytical aspects of anti-inflation policy. The American Economic Review, 50(2), 177-194. Sarel, M. (1996). Nonlinear effects of inflation on economic growth. Staff Papers, 43(1), 199-215. Serven, L., & Solimano, A. (1993). Economic adjustment and investment performance in developing countries: The experience of the 1980s. Striving for Growth after Adjustment: The Role of Capital Formation, 147-180. Sidrauski, M. (1967a). Rational Choice and Patterns of Growth in a Monetary Economy. American Economic Review, 57 (5), 534-544. Sidrauski, M. (1967b). Inflation and economic growth. Journal of political economy, 75(6), 796-810. Singh, K., & Kalirajan, K. (2003). The inflation-growth nexus in India: an empirical analysis. Journal of Policy Modeling, 25(4), 377-396. Singh, P. (2010). Searching threshold inflation for India. Economics Bulletin, 30(4), 3209-3220. Stockman, A. C. (1981). Anticipated inflation and the capital stock in a cash in-advance economy. Journal of Monetary Economics, 8(3), 387-393. Thanh, S. D. (2015). Threshold effects of inflation on growth in the ASEAN-5 countries: A Panel Smooth Transition Regression approach. Journal of Economics, Finance and Administrative Science, 20(38), 41-48. Tobin, J. (1965). Money and economic growth. Econometrica: Journal of the Econometric Society, 671-684. Tobin, J. (1972). Friedman's theoretical framework. Journal of Political Economy, 80(5), 852-863. Tokuoka, K. (2012). Does the Business Environment Affect Corporate Investment in India? (No. 12-70). International Monetary Fund. Ungar, M., & Zilberfarb, B. Z. (1993). Inflation and its Unpredictability--Theory and Empirical Evidence. Journal of Money, Credit and Banking, 25(4), 709-720. Vaona, A., & Schiavo, S. (2007). Nonparametric and semiparametric evidence on the long-run effects of inflation on growth. Economics Letters, 94(3), 452-458. Vasudevan, A., Bhoi, B. K., & Dhal, S. C. (1998). Inflation rate and optimal growth: Is there a gateway to nirvana. Fifty Years of Developmental Economics: Essays in Honour of Prof. Brahmananda, 50-67. Vinayagathasan, T. (2013). Inflation and economic growth: A dynamic panel threshold analysis for Asian economies. Journal of Asian Economics, 26, 31-41.
8. Appendix | Table A1: Investment Rate Models | Dep. Var. →
Exp. Var.↓ | inv_rate | inv_rate | inv_rate | inv_rate | | inv_rate(-1) | 0.938***
(0.0129) | 0.933***
(0.0143) | 0.939***
(0.0128) | 0.933***
(0.0142) | | Inflation^2 | -0.000514**
(0.000189) | -0.000452**
(0.000218) | -0.000510**
(0.000188) | -0.000447*
(0.000216) | | Inflation | 0.00761
(0.0148) | 0.00536
(0.0159) | 0.00713
(0.0146) | 0.00486
(0.0158) | | CAD | 0.0319**
(0.0130) | 0.0381***
(0.0102) | 0.0318**
(0.0129) | 0.0383***
(0.0102) | | FD | -0.134***
(0.0273) | -0.136***
(0.0263) | -0.133***
(0.0270) | -0.136***
(0.0261) | | ToT |
| 1.070
(1.081) |
| 1.104
(1.073) | | Δlnoilprice |
|
| 0.0937
(0.118) | 0.0884
(0.117) | | Constant | 1.786***
(0.374) | 0.874
(0.977) | 1.771***
(0.365) | 0.831
(0.964) | | Within-R2 | 0.9317 | 0.9319 | 0.9317 | 0.9320 | | Country FE | Y | Y | Y | Y | | Year FE | N | N | N | N | | N | 1244 | 1212 | 1244 | 1212 | | Note: Standard errors in parentheses; * p < 0.10, ** p < 0.05, *** p < 0.01. |
| Table A2: IOCR - Final Model | Dep. Var. →
Exp. Var.↓ | IOCR | | IOCR(-1) | 0.828***
(0.0312) | | Inflation | 0.000700**
(0.000270) | | CAD | -0.00341***
(0.000640) | | FD | 0.00102
(0.000933) | | Constant | 0.0150***
(0.00471) | | Within-R2 | 0.7438 | | Country FE | Y | | Time FE | Y | | N | 1241 | | Note: Standard errors in parentheses; * p < 0.10, ** p < 0.05, *** p < 0.01. |
| Table A3: Alternative Specifications as Robustness Checks | | | Full Sample (with ToT) | EME (with ToT) | Oil importing countries | Dep. Var. →
Exp. Var. ↓ | GDPg | GDPg | GDPg | | Inf^3(-1) | 0.00000934
(0.0000161) | 0.00000360
(0.0000210) | 0.0000724***
(0.0000143) | | Inf^2(-1) | 0.00428
(0.00485) | 0.00764
(0.00457) | -0.00988***
(0.00162) | | Inf(-1) | -0.236
(0.302) | -0.569**
(0.255) | 0.252***
(0.0611) | | CAD^2(-1) | 0.00460*
(0.00255) | 0.0121***
(0.00272) | -0.00358
(0.00345) | | FD^2(-1) | -0.00455
(0.00414) | -0.00480
(0.0126) | -0.00787
(0.00517) | | FD(-1)*Inf^2(-1) | -0.0000274
(0.000126) | -0.0000941
(0.000119) | 0.000216
(0.000150) | | FD(-1)*Inf(-1) | -0.00908
(0.00792) | -0.00109
(0.00864) | -0.0161*
(0.00837) | | CAD(-1)*Inf^2(-1) | -0.0000118
(0.0000664) | 0.0000764
(0.0000536) | -0.000166
(0.000147) | | CAD(-1)*Inf(-1) | -0.00261
(0.00516) | -0.0127***
(0.00394) | 0.0228**
(0.00847) | | FD(-1)*CAD(-1) | -0.0193***
(0.00585) | -0.0295***
(0.00683) | -0.00793
(0.00492) | | FD(-1) | -0.773*
(0.442) | -1.756***
(0.294) | -0.0662
(0.0757) | | CAD(-1) | 0.0248
(0.248) | 0.612***
(0.134) | -0.218***
(0.0430) | | ToT(-1) | -2.962
(2.314) | -10.22***
(2.376) |
| | ToT(-1)*Inf^2(-1) | -0.00683*
(0.00395) | -0.00978***
(0.00318) |
| | ToT(-1)*Inf(-1) | 0.357
(0.305) | 0.732***
(0.252) |
| | ToT(-1)*CAD(-1) | -0.0624
(0.242) | -0.461***
(0.144) |
| | ToT(-1)*FD(-1) | 0.628
(0.500) | 1.454***
(0.336) |
| | Constant | 6.394***
(2.182) | 14.09***
(2.302) | 4.122***
(0.395) | | adj. R2 | 0.37 | 0.49 | 0.37 | | N | 1185 | 632 | 895 | | Note: Standard errors in parentheses; * p < 0.10, ** p < 0.05, *** p < 0.01; Country FE = Yes; Time FE = Yes. |
| Table A4: Redundant Variables and Wald Test | | Redundant Variables Test | | | Value | df | Probability | | F-statistic | 2.321000 | (2, 822) | 0.0988 | | Likelihood ratio | 5.107604 | 2 | 0.0778 |
| Wald Test: | | | Equation: FIXEDEFF
Null Hypothesis: C(2)=C(3)=0 | | Test Statistic | Value | df | Probability | | F-statistic | 2.321000 | (2, 822) | 0.0988 | | Chi-square | 4.642000 | 2 | 0.0982 |
| Table A5: Full Sample Panel GMM Estimates for Robustness Check | Dependent variable →
Explanatory variable ↓ | GDPg | | GDPg(-1) | 0.2810082***
(0.0776342) | | Inf^3(-1) | 0.0001463**
(0.0000782) | | Inf^2(-1) | -0.0047006
(0.0062644) | | Inf(-1) | -0.013463
(0.1229162) | | CAD^2(-1) | 0.0214922
(0.0134462) | | FD^2(-1) | -0.118229***
(0.0297729) | | FD(-1)*Inf^2(-1) | -0.0038194***
(0.0008908) | | FD(-1)*Inf(-1) | 0.1325647***
(0.0389756) | | CAD(-1)*Inf^2(-1) | 0.0009749***
(0.0002443) | | CAD(-1)*Inf(-1) | -0.0789433***
(0.0170682) | | FD(-1)*CAD(-1) | 0.1081072***
(0.0417617) | | FD(-1) | 0.1706503
(0.2399486) | | CAD(-1) | 0.2650698*
(0.142881) | | Constant | 2.01***
(0.35) | | Wald Chi-2 | 707.52*** | | N | 1241 | | AR(1) test (p > z) | 4.03 (0.00) | | AR(2) test (p > z) | 1.03 (0.30) | | Sargan test (p > chi2) | 51.03 (0.013) | | Note: Standard errors in parentheses; * p < 0.10, ** p < 0.05, *** p < 0.01; |
Table A6: Threshold Inflation and Growth Rates based on GMM Estimates
(Full Sample) | FD
(as % of GDP) | CAD
(as % of GDP) | Threshold inflation (%) | Growth rate (%) | | 3.00 | 2.00 | 9.36 | 4.76 | | 3.00 | 2.50 | 7.84 | 4.80 | | 3.00 | 3.00 | 6.27 | 4.90 | | 4.00 | 2.00 | 11.65 | 5.30 | | 4.00 | 2.50 | 10.54 | 5.32 | | 4.00 | 3.00 | 9.39 | 5.38 | | 5.00 | 2.00 | 12.99 | 5.69 | | 5.00 | 2.50 | 12.14 | 5.72 | | 5.00 | 3.00 | 11.27 | 5.79 | | 6.00 | 2.00 | 13.84 | 5.87 | | 6.00 | 2.50 | 13.17 | 5.93 | | 6.00 | 3.00 | 12.47 | 6.02 | | Source: Authors’ estimates. |
|