Press Release RBI Working Paper Series No. 04 Does Offshore NDF Market Influence Onshore Forex Market? Evidence from India Harendra Behera, Rajiv Ranjan and Sajjid Chinoy@ Abstract *The paper uses a VECM-MGARCH approach to examine the interrelationship between onshore and offshore NDF markets for the Indian Rupee in view of price discovery, mean and volatility spillovers. The empirical results suggest a stable long-run relationship between onshore and NDF markets with price discovery taking place in spot and forward markets. The sub-period analysis finds short-term mean spillover effects from NDF markets to onshore spot, forward and futures markets during the stress period. Regarding “volatility spillover”, the analysis from the full sample indicates a unidirectional volatility spillover from spot and forward segments to NDF markets in normal circumstances, which turns bi-directional during times of depreciation pressure on the rupee. On the other hand, the existence of two-way volatility spillovers between futures and NDF segments becomes unidirectional from offshore to onshore during episodes of intensified global risks. Moreover, the magnitude of volatility spillovers from offshore to onshore markets also increases during periods of stress. Thus, a real-time monitoring of the market is essential to contain any substantial spillover from the offshore NDF markets. JEL Classification: E44; F31; G14, C32 Keywords: NDF, offshore market, foreign exchange market, MGARCH, spillover Introduction Emerging market economies (EMEs) have, in general, experienced a sharp and sustained rise in trade and capital flows over the last three decades, reflecting a confluence of factors: improved domestic economic prospects, liberalisation of their external sectors, and a gush of global liquidity that advanced economy central banks have injected by aggressively expanding their balance sheets after the global financial crisis. This has commensurately raised non-resident interest in emerging market currencies, both for risk management and speculative ends. The electronification of trading has provided a further boost to demand for EME currencies (Wooldridge, 2019). Rising interest in these currencies, however, is often offset by capital controls and underdeveloped onshore financial markets. All these developments have given birth to a parallel market for EME currencies in offshore centres known as non-deliverable forward (NDF) markets. In NDF markets, trading is settled in a convertible currency, usually in US dollar, as non-convertible currencies are restricted to be delivered offshore. As documented by a report of the RBI (2019), the rising prominence of NDF markets could be mainly on account of restrictions on foreign exchange transactions, cumbersome documentation and Know-Your-Customer (KYC) requirements, restrictions on market participants (especially, non-residents) in hedging activities, cancellation and re-booking of contracts, permission to participate in various existing derivatives product offered by the market regulators, and inconvenient market hours for those in other time zones. Over the years, trading in EME currencies in offshore centres has increased significantly. As per the latest Triennial Survey of the BIS (2019), for example, turnover in offshore markets for the Indian rupee outpaced that of the onshore market. Strong surge in NDF trades were also seen in the case of Brazilian Real (BRL), Taiwanese New Dollar, Indonesian Rupiah (IDR) and Philippine Peso (PHP). When the offshore market volume is significant or larger than that of the onshore market, price discovery can get fragmented wherein domestic market price discovery becomes vulnerable to influences from price discovery in the offshore market. The presence of a large offshore market, therefore, sometimes dilutes the effectiveness of exchange rate management by a central bank and/or hinders the pursuit of domestic financial stability objectives. Against the aforementioned backdrop, this paper tries to examine the relationship1 between onshore and offshore markets for the Indian rupee, and whether there is a long-run relationship between the two markets? Second, if so, what is the degree and directionality of influence? Third, whether the volatility in the onshore market is driven by that of the offshore market? Fourth, if so, how does this change over different time periods – in “normal times” versus “stressed times”? The remaining part of the paper is organised as follows. Section II reviews the literature, while Section III presents some stylised facts of the INR NDF market. A theoretical background behind our empirical analysis is outlined in Section IV, while methodological details are provided in Section V. Data and our empirical results are discussed in Section VI. II. Review of Literature The origin of the NDF market actually dates back to 1970s in response to the capital controls in Australia (Debelle et al., 2006). These markets then started growing in Latin American countries during the 1990s and subsequently expanded rapidly in Asia and Eastern Europe. Analysts and policymakers began recognizing the presence of NDF markets and their inter-relationship with onshore market across several countries and regions, including Asian currencies (Ma et al., 2004; Colavecchio and Funke, 2008; Gu and McNelis, 2013; Ma and McCauley, 2013), the Korean Won (Park, 2001), the Indonesian Rupiah (Cadarajat and Lubis, 2012), the Chinese Yuan (Fung et al., 2004; Colavecchio and Funke, 2008; McCauley and Shu, 2019) and the Indian Rupee (Misra and Behera, 2006; Guru, 2009; Behera, 2011; Goyal et al., 2013; Kumar and Jain, 2018). Various empirical studies found an impact of NDF markets on the onshore forward market (Park, 2001; Wang et al., 2007; Cadarajat and Lubis, 2012), onshore spot market (Behera, 2011, Goyal et al., 2013) and onshore futures market (Behera, 2011). Conversely, a few studies found evidence of the domestic market influencing the NDF market (Wang et al., 2007; Misra and Behera, 2006). More recently, a comprehensive analysis by Schmittmann and Teng (2020) finds a one-way influence from NDFs to onshore markets. While there is a meaningful and growing literature trying to empirically ascertain price linkages between the onshore and offshore markets around the world, the literature that focuses on India remains sparse, dated and inconclusive. For example, Misra and Behera (2006) find that it’s the onshore markets that largely influenced the NDF market, between 2004 to 2007, largely because of restricted participation of domestic players in the offshore market. In a subsequent study, Behera (2011) found that there are volatility spillovers from the NDF market to spot and forward markets in India and the magnitude of volatility spillover has become higher after the introduction of currency futures in 2008. Guru (2009) and Saravanan and Shanmugam (2014) find qualitatively similar results with the role of currency futures in India. Darbha (2012) finds that offshore markets play an important role in price discovery. Kumar and Jain (2018) investigate the interrelationship between spot, forward and NDF markets and conclude that the relationship between the three markets is dynamic owing to the policy measures taken by RBI to curb volatility. Finally, Goyal et al. (2013) find a long-term relationship between NDF and onshore markets, and provide the evidence that the relationship is bidirectional, as both markets adjust to any deviations from the equilibrium state. Their study also finds that shocks originating in the NDF market carry more information during periods of depreciation, leading to mean and volatility spillovers in corresponding on-shore segments. As against the above background, the evidence on India is patchy, inconclusive and largely dated. This paper, therefore, attempts to build on the findings from Chapter 3 of the Report of the Task Force on Offshore Rupee Markets (Chairperson: Usha Thorat) and add to the evidence on this topic by analysing a larger data-set, using more advanced econometric techniques (VECM-MGARCH vs. VAR-MGARCH), as well as leveraging the latest information from the BIS Triennial Survey. III. Stylised Facts India’s onshore foreign exchange (forex) market is primarily a wholesale market, dominated by banks, forex brokers and corporate clients. Individuals, the government and the central bank generally transact through banks. Forex trading typically takes place over-the-counter (OTC) for spot, forward and swaps, while options and futures are traded on exchanges, i.e., National Stock Exchange (NSE), Bombay Stock Exchange (BSE) and Metropolitan Stock Exchange of India Ltd. (MSE). While clearing and settlements are predominantly decentralised, the Clearing Corporation of India Ltd. (CCIL) has started providing a centralised electronic forex trading platform – FX-Retail – for individual and small and medium enterprise customers effective from August 5, 2019. In case of currency futures and option contracts, the clearing houses of respective exchanges act as counterparty to all contracts and set margin requirements. 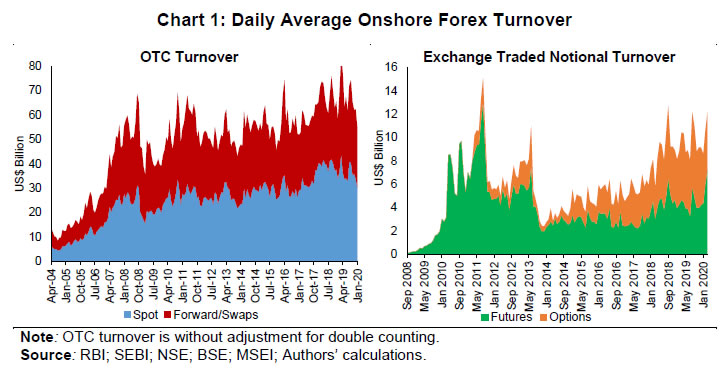 Market participants have also been offered with greater flexibility to undertake foreign exchange operations and to manage their risks. This has been facilitated through simplification of procedures, development of market infrastructure, availability of several new products and extension of forex transaction timings beyond onshore market hours. As a result of various measures over last two decades, liquidity in the foreign exchange market increased significantly. The average daily OTC turnover has increased from about USD 5 billion in 2004 to USD 34 billion in 2019 (Chart 1). Similarly, exchange traded forex derivatives have also shown exponential growth though the daily average turnover still remains much lower at about USD 9.5 billion during 2019 and about USD 12.2 billion in March 2020. 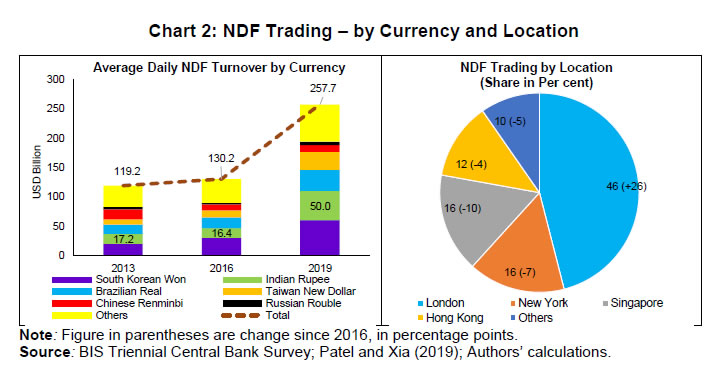 As compared to the onshore market, the turnover in offshore rupee markets has more than tripled between 2016 and 2019 (Chart 2). In fact, the INR NDF turnover at USD 50 billon, exceeded the combined OTC and exchange traded forex turnover of USD 48.8 billion in April 2019. The share of the Indian rupee in the global NDF turnover has also increased significantly from 12.6 per cent in 2016 to 19.4 per cent in 2019 whereas the growth in turnover during this period was more than 200 per cent (Table 1). As reported by the BIS Triennial Central Bank Survey (2019), the turnover in NDFs has almost doubled between 2016 and 2019, mainly driven by the Korean won, Indian rupee, Brazilian real and New Taiwan dollar. The surge in offshore market turnover is likely attributable to the transformation of NDFs from a decentralised and bilateral microstructure to centralised trading with greater disclosure and better clearing system (McCauley and Shu, 2016). The rise in demand for emerging market assets and the electronification of trading providing access to a wider range of market participants has also contributed to the recent surge in NDF turnover (Patel and Xia, 2019). Given the time zone differences and advanced infrastructure availability, the maximum trading in NDF currencies takes place in few international financial centres like London, Singapore and New York. | Table 1: Average Daily NDF Market Turnover | | (USD Million) | | | 2013 | 2016 | 2019 | | Brazilian Real | 15,894 | 18,653 | 35,746 | | Chinese Renminbi | 17,083 | 10,359 | 11,768 | | Indian Rupee | 17,204 | 16,427 | 50,018 | | South Korean Won | 19,565 | 30,075 | 60,103 | | Russian Rouble | 4,118 | 2,926 | 5,497 | | Taiwan New Dollar | 8,856 | 11,504 | 30,865 | | Others | 36,458 | 40,279 | 63,726 | | Total (against USD) | 119,178 | 130,224 | 257,723 | | Total (all currencies) | 127,309 | 134,012 | 258,790 | | Memo | | | | | Share of Indian Rupee (%) | 14.4 | 12.6 | 19.4 | | Source: BIS Triennial Central Bank Survey; Authors’ calculations. | The rise in offshore trading can disrupt the price discovery process of exchange rates in onshore market. Patel and Xia (2019) find a bidirectional relationship between the onshore and offshore markets during normal times but with the offshore market driving movements in the onshore markets during times of global stress. This raises challenges for central banks to manage exchange rates given large offshore volumes. It can be seen from Chart 3 that there is always some gap between the exchange rates of the Indian rupee (INR) in onshore and offshore markets, due to capital account restrictions, transaction costs and basis risk. Moreover, the contracts with shorter maturity have maximum liquidity, accounting for about 70 per cent of overall turnover, reflecting the speculative positions (Kumar and Rituraj, 2020). Large spread between onshore and offshore market encourages market players to take arbitrage advantage while speculative activity in the market result in wide divergences. The large spread between INR NDF rate and INR futures/forward rate can influence the spot rates significantly. As found by Misra and Behera (2006), there are volatility spillovers from NDF market to spot and forward market. In the presence of large spreads in futures and forwards segments as alluded earlier, it is important to understand their relationship. With the Indian Rupee’s “Forward” price being determined across segmented markets – both the onshore deliverable forward market and the offshore non-deliverable market – the key is to ascertain the relative importance of each of these markets in driving “price discovery”. However, simply using (offshore versus onshore) volumes as a means to proxy relative price discovery is imperfect at best. The ability of NDF volumes to drive price discovery, for any given quantum of volumes, is ultimately a function of how inter-connected onshore and offshore markets are, and the ability of economic agents – hedgers, arbitrageurs, speculators – to link these markets. For example, if NDF markets have grown sharply, but it is found that price linkages between the two markets are still tenuous or have not increased commensurately with volumes, – say, because arbitrage opportunities between the two markets have not grown in tandem – then the growth of NDF markets, and the consequent “loss of control” will be of less concern to Indian policymakers. Conversely, if price linkages have grown over time – proportionately to volume increases – then policymakers would rightly worry about the growing role of NDF markets in driving price discovery. In view of the above, the fundamental motivation of this paper is, therefore, to empirically examine price linkages between the NDF and onshore markets, as this is the ultimate manifestation of the influence that NDF markets exert. Given the objective of the paper, the following section deliberates the theory behind the interlinkages between offshore and onshore exchange rates. IV. Theoretical Background The relationship between onshore and offshore markets can be drawn from covered interest parity (CIP) condition which holds when countries do not have capital controls. Therefore, no arbitrage opportunity is possible in the absence of capital control and the forward rate essentially represents the interest rate differential between two currencies. Symbolically: where F is the forward rate, S is the spot rate, r is the interest rate on the home currency and r$ is interest rate on foreign currency (e.g., US dollar). However, the deviation of CIP has been observed for the countries with some forms of capital controls. Under such condition, F only can be approximated by the above equation as: The existence of currency convertibility restrictions, making the markets inefficient, provides opportunity to the arbitragers and speculators to earn profits by taking positions on the currency. Hence, the NDF rate should be anchored by the onshore forward rate to the extent that arbitragers can link these markets:  In case of CIP violation in the presence of capital account restrictions, a trader can earn arbitrage profits by borrowing in low yielding currency, converting the proceeds into the high yielding currency in the spot market and lending the same, and converting back it to the original currency using a forward contract if forward rate deviates from CIP. This is possible through carry trade or taking position in an offshore center and settling the difference through a convertible currency. The extent of CIP violation could be much larger during global uncertainty situation due to significant rise in counter-party credit risk and liquidity constraints (Coffey et al., 2009), even in case of convertible currency. As a result, the volatility spillover increases between markets during the times of heightened uncertainty. Furthermore, the sign of the onshore-offshore yield spread can indicate the underlying market pressure on the currency. If the domestic interest rate is higher than the NDF implied yield, it implies appreciation pressures on the currency. However, capital controls may restrict inflows to close the gap. Similarly, a lower domestic interest rate than implied by the NDF yield would suggest depreciation pressures, while a zero spread would likely reflect an absence of market pressure on both the domestic and offshore market. Generally, it is expected that there is a long-run relationship between both onshore and offshore markets and there is the likelihood of “mean” spillovers on a regular basis. Furthermore, hedging, arbitrage and speculative activities may also result in volatility spillovers from one market to another on various occasions. IV.1. Testing for “Mean” and “Volatility” Spillovers We start, therefore, by empirically testing for linkages between onshore (spot, forward and futures prices) and offshore (NDF forward prices) markets. The goal is to assess: -
Whether there is a stable long-term relationship between onshore and offshore markets? -
Do onshore prices drive offshore prices? Or vice versa? Or both? -
To see whether the direction of influence is a function of context? Are the results different for “normal” times versus “stressed periods” (i.e., taper tantrum, emerging market stress)? -
Whether there are volatility spillovers between onshore and offshore markets? What are the degree and direction of the spillover? V. Methodology V.I. VECM-MGARCH Framework A two-step procedure is followed to examine the relationship between onshore and offshore exchange rates of the Indian rupee. First, a vector error correction model (VECM) is used to study the long-run and short-run dynamics of the two markets. In the second step, a bivariate BEKK-GARCH (1,1) model, as proposed by Engle and Kroner (1995), is estimated. Our choice for using BEKK-GARCH model was prompted by its advantage over other multivariate conditional volatility models in ensuring positive definitiveness. In the model, the system of conditional mean equations follow from the VECM specification as given in eq. (3) and conditional variance equation as in eq.(4). 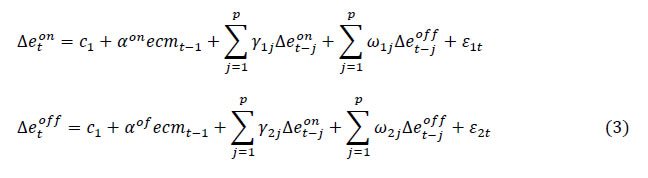
 From eq. (3), we get residuals, ε1t and ε2t, which are then used in the second stage to estimate the variance and co-variance equations. Taking into account the asymmetric responses, i.e., volatility tends to increase more in response to negative shocks (bad news or large depreciations of the rupee) than positive shocks (good news or appreciations), in the variances and covariances, as proposed by Kroner and Ng (1998), a BEKK representation of conditional variance equation can be written as: 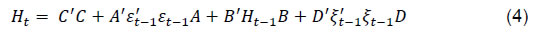
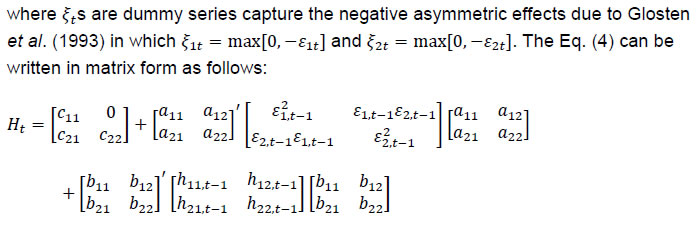
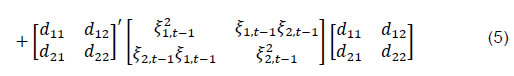 In the above model, the dynamic process of Ht is a linear function of its own lagged values, lagged squared innovations and the cross-product of the innovations, and asymmetric terms. Volatility transmission between onshore and offshore markets is represented by the off-diagonal parameters in matrices A and B while the diagonal parameters in those matrices capture the effects of their own past shocks and volatility. The diagonal parameters in matrix D measure the response of own past negative shocks while the off-diagonal parameters dij show the response of one market to the negative shocks in another market, called the cross-market asymmetric responses. V.II. Granger Causality Tests The causality in conditional means is tested in exactly the same way as mentioned in the previous sub-section. The only difference here is that the test is performed after simultaneous estimation of eq. (3) and eq. (4) whereas, in the earlier case, the test was conducted after estimating eq. (3) only. Specifically, we test the joint significance of parameters αon and ω1j being different from zero to study mean spillovers from offshore to onshore markets up to the pth lag and vice-versa if αof and ω2j are non-zero. The no-causality in variance test, based on cross-correlation function (CCF) of squared residuals of univariate GARCH model of Cheung and Ng (1996), extended to multivariate framework following Caporale et al. (2002). Tests for causality-in-variance is performed by constraining the matrices A, B and D to be upper triangular and lower triangular, thereby permitting for causality in either direction. The causality-in-variance is checked employing likelihood ratio test for the null hypotheses of no causality-in-variance from offshore to onshore (H0: a12 = b12 = d12 = 0) and no causality-in-variance from onshore to offshore (H0: a21 = b21 = d21 = 0) considering the asymmetric effects. However, d12 and d21 can be dropped from the tests to know the causality without asymmetry response2. VI. Data and Empirical Results Closing prices of USD/INR exchange rates (as per the Indian timestamp in Thomson Reuters Eikon) for the period January 1, 2005 through December 31, 2019 have been used in this paper. The daily exchange rates are spot, forward, futures and NDF of 1-month maturity, and are expressed in natural log forms after converting them to USDs per Indian rupee. Here, the offshore market is represented by the NDF rate whereas the other three exchange rates are onshore rates. Summary statistics of annualised exchange rate returns are displayed in Table 2. Here, data is presented from 2009 through the empirical exercises are conducted using data from 2005-2019. The results show exchange rate depreciation in each year except 2009, 2010 and 2017. The average return in the offshore market is not statistically different from that of the onshore market. However, the volatility in the NDF market is significantly higher than that in onshore segments. The result also reveals a rise in volatility during 2010-2013, which has come down over the years except in 2018. The correlation coefficient of the annualised exchange rate returns is statistically significant and large in size, while the degree of correlation declines during the years of excess volatility. All these results provide preliminary evidence of volatility spillovers from offshore to onshore markets. However, volatility transmission to onshore market might have increased as can be inferred from high volatility during 2013 despite low correlation coefficient on account of lead and lag in relationship and time zone differences. These preliminary results create the need for a deeper analysis of the relationship between onshore and offshore markets. | Table 2: Summary Statistics | | Period | Mean | Satterthwaite-Welch Test | Volatility | Levene Test | Correlation | | Spot | Forward | Futures | NDF | Spot | Forward | Futures | Spot | Forward | Futures | NDF | Spot | Forward | Futures | Spot | Forward | Futures | | 2009 | 5.4 | 5.5 | 5.0 | 5.4 | 0.998 | 0.995 | 0.976 | 157.9 | 157.4 | 146.4 | 166.0 | 0.70 | 0.65 | 0.09 | 0.84 | 0.84 | 0.78 | | 2010 | 4.0 | 3.7 | 4.0 | 4.1 | 0.993 | 0.971 | 0.989 | 124.2 | 125.5 | 124.8 | 133.4 | 0.53 | 0.70 | 0.31 | 0.79 | 0.79 | 0.73 | | 2011 | -16.7 | -16.9 | -17.2 | -17.7 | 0.934 | 0.942 | 0.965 | 126.9 | 126.8 | 120.9 | 143.6 | 0.16 | 0.15 | 0.04 | 0.79 | 0.79 | 0.72 | | 2012 | -3.2 | -3.2 | -2.7 | -1.5 | 0.909 | 0.911 | 0.939 | 157.8 | 157.7 | 158.9 | 174.1 | 0.27 | 0.28 | 0.26 | 0.86 | 0.86 | 0.79 | | 2013 | -10.9 | -11.1 | -11.2 | -11.7 | 0.965 | 0.970 | 0.977 | 195.9 | 196.0 | 188.4 | 201.4 | 0.49 | 0.47 | 0.19 | 0.71 | 0.71 | 0.68 | | 2014 | -1.8 | -1.7 | -1.8 | -2.0 | 0.986 | 0.978 | 0.988 | 94.9 | 94.5 | 100.9 | 111.6 | 0.01 | 0.01 | 0.06 | 0.64 | 0.64 | 0.47 | | 2015 | -4.7 | -4.6 | -4.4 | -4.2 | 0.950 | 0.964 | 0.983 | 93.0 | 93.2 | 92.4 | 103.6 | 0.20 | 0.25 | 0.02 | 0.92 | 0.92 | 0.67 | | 2016 | -2.5 | -2.3 | -2.4 | -2.4 | 0.986 | 0.993 | 0.995 | 79.9 | 79.8 | 78.4 | 86.5 | 0.24 | 0.26 | 0.05 | 0.94 | 0.94 | 0.57 | | 2017 | 6.3 | 6.3 | 6.2 | 6.4 | 0.988 | 0.983 | 0.968 | 65.8 | 65.5 | 67.6 | 72.2 | 0.07 | 0.06 | 0.16 | 0.79 | 0.79 | 0.62 | | 2018 | -8.4 | -8.4 | -8.5 | -8.3 | 0.997 | 0.997 | 0.986 | 106.2 | 106.7 | 105.1 | 119.5 | 0.03 | 0.04 | 0.05 | 0.78 | 0.78 | 0.69 | | 2019 | -2.4 | -2.3 | -2.2 | -2.2 | 0.983 | 0.986 | 0.998 | 94.0 | 93.9 | 94.0 | 101.7 | 0.32 | 0.30 | 0.08 | 0.85 | 0.85 | 0.65 | Full Sample
(2009 to 2019) | -3.2 | -3.2 | -3.2 | -3.1 | 0.982 | 0.982 | 0.975 | 123.6 | 123.7 | 121.2 | 133.9 | 0.00 | 0.00 | 0.00 | 0.80 | 0.80 | 0.70 | Note: The null hypothesis is equality of mean and variance of annualised exchange rate changes between onshore and offshore segments of the forex market, respectively, in Satterthwaite-Welch test and Levene test, respectively. Correlation coefficients are calculated between annualised returns of NDF onshore exchange rates for each year.
Source: Authors’ calculations. |
| Table 3: Unit Root Test Results | | | Level | First Difference | | Variables | ADF | PP | KPSS | ADF | PP | KPSS | | With only intercept | | | | | | | | Spot | -0.46 | -0.51 | 7.20* | -26.02* | -61.89* | 0.08 | | Forward | -0.47 | -0.51 | 7.21* | -25.91* | -61.76* | 0.07 | | Futures | -1.23 | -1.26 | 6.38* | -64.39* | -52.78* | 0.06 | | NDF | -0.63 | -0.61 | 7.20* | -40.16* | -64.39* | 0.06 | | With trend and Intercept | | | | | | | | | -2.49 | -2.44 | 0.57* | -26.02* | -61.89* | 0.06 | | Forward | -2.49 | -2.43 | 0.56* | -25.91* | -61.76* | 0.06 | | Futures | -2.16 | -2.33 | 0.64* | -40.15* | -52.77* | 0.04 | | NDF | -2.57 | -2.49 | 0.55* | -64.39* | -64.39* | 0.05 | Note: Null hypothesis is 'Series has a unit root' in Augmented Dickey Fuller (ADF) and Phillips-Perron (PP) tests while it is 'Series does not have a unit root' in Kwiatkowski-Phillips-Schmidt-Shin(KPSS) test. *: Significant at less than 5 per cent level.
Source: Authors’ calculations. |
| Table 4: Johansen Cointegration Test Results | | Null hypothesis | Spot and NDF | Forward and NDF | Futures and NDF | | λtrace (r) | λmax (r) | λtrace (r) | λmax (r) | λtrace (r) | λmax (r) | | r=0 | 112.04*** | 111.85*** | 146.57*** | 146.37*** | 236.35*** | 235.06*** | | r=1 | 0.19 | 0.19 | 0.20 | 0.20 | 1.29 | 1.29 | Note: λtrace (r) tests the null hypothesis of at most ‘r’ cointegrating relationships against the alternative that the number of cointegration vectors is greater than ‘r’. λmax(r) tests the null hypothesis of ‘r’ cointegrating relationships against the alternative of‘ ‘r+1’ cointegration vectors.
***: Significant at 1 per cent level.
Source: Authors’ calculations. |
| Table 5: ECM and Long-run Coefficients | | Variables | Full Sample
(Jan 1, 2005 to
Dec 31, 2019) | Sub-sample 1 | Sub-sample 2 | Sub-sample 3 | Sub-sample 4 | Sub-sample 5 | Jan 1, 2005
to
Sep 8, 2008 | Sep 9, 2008
to
Apr 23, 2012 | Apr 24, 2012
to
Nov 11, 2014 | Nov 12, 2014
to
Sep 30, 2017 | Oct 1, 2017
to
Dec 31, 2019 | | | β | αon | αoff | β | αon | αoff | β | αon | αoff | β | αon | αoff | β | αon | αoff | β | αon | αoff | | Spot & NDF | 1.001 | -0.029 | 0.143 | 1.014 | 0.016 | 0.249 | 0.966 | -0.078 | 0.173 | 0.986 | -0.407 | 0.021 | 0.991 | -0.212 | 0.311 | 0.996 | -0.362 | 0.187 | | (700.0)** | -(1.18) | (5.02)** | (129.3)** | (0.46) | (5.61)** | (98.0)** | -(1.69)* | (3.25)** | (216.2)** | -(5.07)** | (0.22) | (315.0)** | -(2.09)** | (2.70)** | (325.4)** | -(3.16)** | (1.39) | | Forward & NDF | 1.006 | -0.044 | 0.18 | 1.014 | -0.059 | 0.301 | 0.974 | -0.096 | 0.167 | 0.996 | -0.449 | 0.03 | 0.989 | -0.279 | 0.262 | 0.995 | -0.494 | 0.17 | | (933.7)** | -(1.56) | (5.45)** | (200.3)** | -(1.35) | (5.42)** | (106.4)** | -(2.01)** | (3.01)** | (245.2)** | -(5.41)** | (0.30) | (341.1)** | -(2.63)** | (2.17)** | (409.3)** | -(3.91)** | (1.14) | | Futures & NDF | 0.999 | -0.214 | 0.20 | | | | 0.980 | -0.19 | 0.196 | 0.991 | -0.577 | -0.13 | 0.989 | -0.394 | 0.06 | 0.996 | -0.437 | 0.182 | (1127.8)
** | -(5.81)** | (4.35) ** | | | | (156.9)** | -(3.87)** | (3.17)** | (254.7)** | -(7.14)** | -(1.29) | (159.5)** | -(8.85)** | (1.06) | (271.7)** | -(5.39)** | (1.83)* | Note: Figures in parentheses are t-statistics.
**, *: Significant at 5 per cent and 10 per cent levels, respectively.
Source: Authors’ calculations. | VI.1. Long-run Causality As expected, the exchange rate series are non-stationary in levels but stationary in first differences as per various unit root test results (Table 3)3. This calls for the examination of any stable long-term relationship between onshore exchange rate series and NDF rate using cointegration test. Johansen maximum likelihood estimation result suggests a unique cointegrating relationship between any of the onshore exchange rate series (spot, forward and futures) and NDF rate as suggested by both λtrace and λmax test statistics (Table 4). Although unit root and cointegration test results discussed above are for the full sample period, we also conduct the analysis on five sub-sample periods.4 The estimated long-run and short-run coefficients are reported in Table 5. The result shows that β is positive, statistically significant and with a magnitude very close to or at 1, implying an almost one-for-one movement across markets in the long run. For example, a 1 per cent increase in NDF rates leads to an almost 1 per cent increase in onshore exchange rates in the long run. More generally, a long-run coefficient close to 1, means that there is no permanent friction between onshore and offshore markets that creates any meaningful gap in the long run. Additionally, β declined during the period that includes the global financial crisis (sub-sample 2) and the taper tantrum (sub-sample 2). While establishing a long-term relationship is important, it will not come as a particular surprise. Instead, the real question is whether onshore prices drive offshore prices, or vice versa? In this context, the coefficients of interest are αon and αoff – the ECM terms. For the full sample period, both the ECM terms have correct signs though αon is statistically insignificant in spot and forward markets. This suggests an equilibrium in the system and that there is a bi-directional relationship between both markets in the long-run. Since αon is statistically insignificant, it may not be incorrect to say that price discovery takes place in spot and forward market rather than in NDF market in the long-run. On the other hand, the price discovery process in futures and NDF markets are influenced by each other. Relatively small β coefficient and larger speed of adjustment indicate about the presence of arbitrage and speculative activity between futures and NDF market as getting information about onshore market is faster through exchange traded products, which further makes speculation easy. This is also reflected in occasional large spread between futures and NDF market (Chart 3). The low magnitude of the speed of adjustment parameters in the full sample and most of the sub-sample periods in other segments suggests a moderate speed of convergence to the long-run equilibrium when a shock causes the system to go into disequilibrium. Given the value of β close to 1, it is not a surprise to find a smaller value for α. For the entire time period, the overall result suggests that both NDF and the onshore exchange rates influence each other, and gradually converge towards their long-term relationship after a shock. The stable long-term relationship between the markets also implies that the central bank intervention does not have any impact on the directional movement of the Indian rupee unlike it is found in the context of China (see Su et al., 2019; Ding et al., 2014). Rather, the intervention impacts the exchange rate fluctuations in onshore market which subsequently influence the offshore rupee movements as reflected in results in mean spillover from onshore to offshore. VI.2. Sub-period Analysis on Long-run Causality Results for the entire time period may not capture how the relationship has changed over time. To explore this further, therefore, we conduct a sub-period analysis to distinguish between periods of stress and normal periods. While sub-sample 2 includes the global financial crisis and the peak of the European debt crisis; taper tantrum episodes are part of sub-sample 3 and the emerging market stress of 2018 is captured in sub-sample 5. These three sub-periods comprise the “stress periods” whereas sub-samples 1 and sub-sample 4 reflect normal times. The sub-sample analysis reveals that αon is statistically significant and correctly signed whereas αoff is statistically insignificant during periods of stress, particularly in sub-samples 3 and 5. Interestingly, the speed of adjustment is much faster for onshore markets during these phases vis-a-vis the full sample as well as other sub-periods. On the other hand, the results also suggest a unidirectional long-run causality from onshore spot and forward to NDF market in sub-sample 1 and bidirectional causality during the normal times (i.e., sub-samples 2 and 4). Interestingly, in the case of futures markets, they were unidirectionally driven by the NDF market in sub-sample 4. What all these evidences suggest is that onshore spot, forward and futures rates were playing very little role in influencing NDF rates during times of stress. More intuitively, this likely reflected the growing volumes – potentially speculative – in the NDF market in times of stress, relative to volumes in the onshore market. This also reduced the efficacy of foreign exchange intervention by the central bank as the effects of intervention on the onshore exchange rate stay up to the end of India’s business hour while the NDF market remains open for 24 hours. Thus, the NDF rates evolve overnight and influence the opening exchange rate in the onshore markets when they open. This reduces effectiveness of previous day’s intervention because there was often little correlation between the closing exchange rate of the previous day and the opening rate of the next day, and therefore necessitated additional intervention the next day. VI.3. Mean and Volatility Spillovers So far, the focus has been on price spillovers where the estimated parameters are based on the assumption of constant error variance. In order to examine the mean and volatility spillovers between the onshore and offshore markets, we estimate an VECM-MGARCH model, as specified in equations (3) and (4), where the error variances are time-varying. This model allows simultaneous interactions of conditional returns and volatilities across the markets. In this modelling framework, we also examine the Granger-causality in mean and variance as previously discussed. The empirical analysis is conducted using daily data from April 1, 2005 through December 31, 2019 of the currency pairs (i) NDF-Spot; (ii) NDF-Forwards; and (iii) NDF-Futures. The analysis is provided for full period as well as for five sub-periods. | Table 6: MGARCH-BEKK Parameter Estimates | | Variable | Spot and NDF | Forward and NDF | Futures and NDF | | Coeff | P-value | Coeff | P-value | Coeff | P-value | | Mean Equation | | ∆On(-1) | -0.372 | 0.00 | -0.378 | 0.00 | -0.291 | 0.00 | | ∆On(-2) | -0.285 | 0.00 | -0.298 | 0.00 | -0.203 | 0.00 | | ∆On(-3) | -0.189 | 0.00 | -0.203 | 0.00 | -0.085 | 0.01 | | ∆On(-4) | -0.107 | 0.00 | -0.125 | 0.00 | -0.075 | 0.01 | | ∆On(-5) | -0.086 | 0.00 | -0.093 | 0.00 | -0.031 | 0.22 | | ∆On(-6) | -0.053 | 0.02 | -0.063 | 0.01 | -0.032 | 0.12 | | ∆Off(-1) | 0.382 | 0.00 | 0.381 | 0.00 | 0.309 | 0.00 | | ∆Off(-2) | 0.251 | 0.00 | 0.262 | 0.00 | 0.140 | 0.00 | | ∆Off(-3) | 0.166 | 0.00 | 0.178 | 0.00 | 0.076 | 0.01 | | ∆Off(-4) | 0.155 | 0.00 | 0.164 | 0.00 | 0.113 | 0.00 | | ∆Off(-5) | 0.114 | 0.00 | 0.126 | 0.00 | 0.059 | 0.02 | | ∆Off(-6) | 0.051 | 0.02 | 0.056 | 0.01 | 0.014 | 0.50 | | Constant | -0.003 | 0.48 | -0.026 | 0.14 | 0.012 | 0.00 | | ecm_on(-1) | -0.022 | 0.32 | -0.039 | 0.12 | -0.322 | 0.00 | | ∆On(-1) | 0.249 | 0.00 | 0.210 | 0.00 | -0.074 | 0.09 | | ∆On(-2) | 0.185 | 0.00 | 0.157 | 0.00 | -0.154 | 0.00 | | ∆On(-3) | 0.124 | 0.00 | 0.107 | 0.01 | -0.131 | 0.00 | | ∆On(-4) | 0.130 | 0.00 | 0.116 | 0.00 | -0.090 | 0.02 | | ∆On(-5) | 0.076 | 0.02 | 0.071 | 0.04 | -0.043 | 0.20 | | ∆On(-6) | 0.042 | 0.11 | 0.027 | 0.34 | -0.010 | 0.69 | | ∆Off(-1) | -0.186 | 0.00 | -0.147 | 0.00 | 0.104 | 0.01 | | ∆Off(-2) | -0.194 | 0.00 | -0.163 | 0.00 | 0.096 | 0.02 | | ∆Off(-3) | -0.136 | 0.00 | -0.113 | 0.00 | 0.137 | 0.00 | | ∆Off(-4) | -0.071 | 0.03 | -0.055 | 0.13 | 0.158 | 0.00 | | ∆Off(-5) | -0.041 | 0.18 | -0.031 | 0.34 | 0.086 | 0.01 | | ∆Off(-6) | -0.052 | 0.04 | -0.040 | 0.12 | 0.013 | 0.63 | | Constant | 0.028 | 0.00 | 0.131 | 0.00 | -0.005 | 0.04 | | ecm_off(-1) | 0.133 | 0.00 | 0.187 | 0.00 | 0.163 | 0.00 | | Variance Equation | | C(1,1) | 0.012 | 0.00 | 0.012 | 0.00 | 0.010 | 0.00 | | C(2,1) | 0.012 | 0.00 | 0.013 | 0.00 | -0.003 | 0.15 | | C(2,2) | 0.004 | 0.00 | 0.004 | 0.00 | 0.012 | 0.00 | | A(1,1) | 0.240 | 0.00 | 0.236 | 0.00 | 0.181 | 0.00 | | A(1,2) | -0.050 | 0.10 | -0.056 | 0.06 | -0.054 | 0.14 | | A(2,1) | 0.018 | 0.40 | 0.024 | 0.24 | -0.031 | 0.28 | | A(2,2) | 0.291 | 0.00 | 0.301 | 0.00 | 0.271 | 0.00 | | B(1,1) | 0.960 | 0.00 | 0.960 | 0.00 | 0.953 | 0.00 | | B(1,2) | 0.005 | 0.61 | 0.005 | 0.62 | 0.052 | 0.00 | | B(2,1) | 0.000 | 0.95 | -0.001 | 0.90 | 0.025 | 0.04 | | B(2,2) | 0.959 | 0.00 | 0.958 | 0.00 | 0.933 | 0.00 | | D(1,1) | -0.115 | 0.02 | 0.101 | 0.03 | 0.156 | 0.00 | | D(1,2) | -0.143 | 0.02 | 0.076 | 0.27 | -0.111 | 0.04 | | D(2,1) | 0.155 | 0.00 | -0.154 | 0.00 | 0.006 | 0.87 | | D(2,2) | 0.111 | 0.02 | -0.071 | 0.175 | 0.074 | 0.093 | | No. of Obs. | 3905 | | 3905 | | 2951 | | | Log-likelihood | 8916.34 | | 9007.84 | | 5871.38 | | | MV-Q (8) | 39.91 | 0.16 | 35.57 | 0.30 | 11.88 | 1.00 | Note: MV-Q refers to multivariate Q test of the standardised residuals for ARCH effects up to lag 8. On: Onshore exchange rates; Off: Offshore NDF rates.
Source: Authors’ calculations. |
| Table 7: Granger-causality in Mean and Variance Test - χ2 Statistics | | Direction of Causality | Full Sample | Sub-Sample | | 1 | 2 | 3 | 4 | 5 | | Causality-in-Mean | | NDF → Spot | 1139.0 (0.00) | 12.3 (0.02) | 64.7 (0.00) | 217.2 (0.00) | 48.6 (0.00) | 55.7 (0.00) | | Spot → NDF | 277.0 (0.00) | 455.5 (0.00) | 18.0 (0.00) | 14.6 (0.01) | 3.4 (0.18) | 4.9 (0.18) | | NDF → Forward | 379.9 (0.00) | 26.4 (0.00) | 58.3 (0.00) | 124.6 (0.00) | 59.7 (0.00) | 95.7 (0.00) | | Forward → NDF | 220.0 (0.00) | 121.2 (0.00) | 50.0 (0.00) | 13.7 (0.01) | 2.1 (0.36) | 2.8 (0.42) | | NDF → Futures | 1120.9 (0.00) | | 200.3 (0.00) | 207.9 (0.00) | 265.3 (0.00) | 155.2 (0.00) | | Futures → NDF | 32.2 (0.00) | | 10.1 (0.04) | 16.1 (0.00) | 0.2 (0.90) | 3.0 (0.39) | | Causality-in-Variance (without asymmetric effect) | | Spot → NDF | 5.3 (0.07) | 16.9 (0.00) | 83.8 (0.00) | 0.3 (0.86) | 2.2 (0.34) | 2.3 (0.32) | | NDF → Spot | 1.5 (0.47) | 13.2 (0.00) | 187.7 (0.00) | 6.1 (0.05) | 2.4 (0.30) | 5.7 (0.06) | | Forward → NDF | 8.3 (0.02) | 16.7 (0.00) | 63.5 (0.00) | 1.3 (0.52) | 1.8 (0.40) | 55.5 (0.00) | | NDF → Forward | 2.7 (0.27) | 10.2 (0.01) | 25.2 (0.00) | 9.4 (0.01) | 3.6 (0.17) | 5.2 (0.07) | | Futures → NDF | 13.9 (0.00) | | 2.5 (0.29) | 54.1 (0.00) | 3.0 (0.22) | 32.1 (0.00) | | NDF → Futures | 4.8 (0.09) | | 8.5 (0.01) | 75.8 (0.00) | 20.7 (0.00) | 15.0 (0.00) | | Causality-in-Variance (with asymmetric effect) | | Spot → NDF | 12.5 (0.01) | 27.7 (0.00) | 88.7 (0.00) | 2.9 (0.40) | 2.3 (0.51) | 4.5 (0.22) | | NDF → Spot | 20.8 (0.00) | 22.2 (0.00) | 201.8 (0.00) | 6.1 (0.10) | 2.6 (0.46) | 10.7 (0.01) | | Forward → NDF | 11.0 (0.01) | 25.8 (0.00) | 76.9 (0.00) | 3.7 (0.29) | 1.8 (0.60) | 61.8 (0.00) | | NDF → Forward | 25.3 (0.00) | 30.7 (0.00) | 45.6 (0.00) | 9.5 (0.02) | 3.6 (0.31) | 16.1 (0.00) | | Futures → NDF | 14.3 (0.00) | | 2.8 (0.42) | 57.2 (0.00) | 7.5 (0.06) | 33.5 (0.00) | | NDF → Futures | 6.0 (0.11) | | 9.4 (0.02) | 78.3 (0.00) | 29.8 (0.00) | 18.6 (0.00) | Note: Figures in parentheses are p-values. Null hypothesis is rejected if the p-value in the Wald test is less than 5 per cent.
Causality-in mean: H0: αon = 0, ω11 = 0, ...ω1j = 0 for offshore to onshore;
H0: αof = 0, γ21 = 0, ...γ2j = 0 for onshore to offshore.
Causality-in variance: H0: a12 = g12 = 0 for onshore to offshore (without asymmetry);
H0: a21 = g21 = 0 for offshore to onshore (without asymmetry).
Causality-in variance: H0: a12 = g12 = d12 = 0 for onshore to offshore (with asymmetry);
H0: a21 = g21 = d21 = 0 for offshore to onshore (with asymmetry).
Source: Authors’ calculations. | The estimated parameters of VECM-asymmetric BEKK model are presented in Table 6 for full sample period and in Appendix (Tables A.2 to A.4) for sub-sample periods. The post-diagnostic statistics are satisfactory as can be observed from the multivariate Q-statistics of ARCH effect and log-likelihoods. The sign, statistical significance and magnitude of the error correction parameter are almost similar as found earlier even after controlling for time-varying variances, for both full sample and sub-sample periods. This result corroborates our earlier findings on long-run causality between the onshore and offshore markets. Mean and volatility spillovers between markets are examined by looking at individual coefficients and Granger causality tests. For the full sample, individual coefficients (γ1j, ω1j, γ2j and ω2j) of exchange rate changes in the mean equation are statistically significant in most of the cases implying a bi-directional mean spillover between the onshore and offshore markets. A similar observation can be made from the results of sub-sample 1, 2 and 3. The lagged coefficients of NDF returns are statistically significant at conventional levels while the coefficients are statistically insignificant for onshore exchange rate returns in sub-periods 4 and 5. This indicates that there was one-way mean spillover from NDF markets to onshore spot, forward and futures markets in the post-taper tantrum period. This finding is important from a policy perspective as onshore market participants were drawing information from the offshore market to form their price behavior which could cause large fluctuations in domestic exchange rates. VI.4. Granger Causality-in-mean Tests The Granger causality-in-mean test results corroborate our earlier findings (Table 7). The null hypothesis ‘the cross terms and the related ECM term are equal to zero (αon = 0, ω11 = 0, ...ω1j = 0)’5 is rejected at less than 5 per cent level of significance, implying mean spillover from offshore to onshore forex markets. The null hypothesis is also rejected for the causality of opposite direction. However, one-way Granger causality-in-mean is found from NDF market to onshore forex market for sub-samples 4 and 5. Based on these results, we conclude that there was a bidirectional mean spillover between onshore and offshore forex markets, which turn unidirectional from offshore to onshore market since 2014. The unidirectional mean spillover from offshore to onshore markets could be due to significant increase in NDF market turnover in last few years. These findings are consistent with the evidences provided earlier in this study and may upshot the exchange rate management policy of the Reserve Bank of India less effective. VI.5. Volatility Spillover In order to understand volatility spillover between these markets, let us discuss the estimated conditional variance results (provided in bottom part of the tables). Across the samples, the estimated diagonal parameters, a11, a22, b11 and b22, are statistically significant at 5 per cent level, signifying a strong GARCH(1,1) process, where volatility is driven by their own past shocks and volatility. The large size of b11 and b22 indicates about strong volatility persistency. The coefficients b12 and b21 measure the direct effect of volatility spillover while a12 and a21 measure indirect effects. For the entire time period, among the off-diagonal parameters, a12 is statistically significant in spot and forward markets but insignificant in futures market; a21 is statistically insignificant in all the segments. The parameters, b12 and b21, are statistically insignificant in spot and forward markets but significant in futures market. Statistical significance of d12 in spot and futures segments suggest that volatility in onshore forex market responds asymmetrically to depreciation pressures in NDF market. Moreover, a statistically significant coefficient d12 indicates that the NDF market also reacts more to the depreciation shocks than the appreciating pressure in spot and futures segments. The overall results provide the evidence of volatility spillovers between NDF and futures markets and the spillover could be greater from NDF to futures segment during the time of depreciation pressure of the rupee in offshore market. VI.6. Granger Causality-in-variance Tests The Granger-causality-in-variance test results are reported with and without asymmetric effects, mainly to identify whether volatility spillover is different during stress periods (Rupee depreciation pressures) versus normal period or periods of appreciation. The results show a unidirectional volatility spillover from spot and forward segments to NDF markets in normal circumstances, but it turns bidirectional in the presence of asymmetric effect. On the other hand, there exists a two-way volatility spillover between futures and NDF segments. The sub-sample analysis suggests a bidirectional causality-in-variance, both with and without presence of asymmetric effects, between onshore market (spot and forward) and offshore market in sub-period 1 and 2. The direction of spillover became unidirectional from offshore to onshore spot market during the taper tantrum period (sub-sample 3) and emerging market turmoil (sub-sample 5) period. The spillover effect was bidirectional between futures and NDF markets during the same period and was unidirectional from NDF to forward segment in taper period. The volatility spillover effect continues to be bidirectional between futures and NDF markets in recent period. The causality-in-variance again turned bidirectional between forward and NDF market during the time of heightened volatility (i.e., sub-sample 5). What is more worrisome is the level of significance increases with the incorporation of asymmetric effects to reject the null of no causality-in-variance from offshore to onshore market. This indirectly implies that the volatility spillover increases from NDF to onshore markets during the periods of heightened uncertainty wherein the rupee faces depreciation pressure due to large capital outflows. Specifically, speculator build up long rupee carry positions in offshore market to make profits from large interest rate differential. With the onset of the global risk-off sentiment, they rush to covering up those positions. The hedgers also book large volume of contracts to protect their future cash flows. As a result, the exchange volatility in the offshore market surges during global uncertainty like taper tantrum and similar events. At the same time, the domestic players frequently look for information on exchange rate movements from overseas NDF market, which gives rise to higher volatility in domestic forex market. VI.7. Time-varying Volatility Across Segments – What Do They Indicate? In order to better understand volatility spillover across markets, it’s important to analyze how volatility in these markets has changed over time. The conditional volatility estimated from the model discussed above for the full sample period is plotted in Chart 4. The volatilities in the spot, forward, futures and NDF display a similar pattern over time. It is pertinent to note that volatility across markets was high during 2006-2014, which has reduced significantly in recent years. The chart also shows a sudden and significant rise in volatility during episodes of US monetary tightening in 2006, global financial crisis, European sovereign debt crisis, taper tantrum and the latter part 2018, coinciding with a rise in offshore-onshore spreads. During these episodes, volatility was much higher in the NDF market as compared to onshore spot, forward and futures markets. Generally, the volatility in NDF markets is also sizeable compared to onshore markets and the divergence between the two gets accentuated in times of heightened uncertainty. This observation mainly reflects the fact that players in the offshore market do not have access to enough information that the domestic market players have and therefore, they react expressively in response to any global shocks that may not have much implications for the domestic economy. Moreover, the volatility in the onshore segments is contained by central bank intervention. However, a rise in volatility in offshore market is ultimately transmitted to onshore forex markets once the domestic market players start reacting to the movements in NDF segment. A closer examination of the data on the volatilities in the two markets shows that volatility increases in offshore market before it rise in onshore markets with a lag of 1 to 2 days. Consequently, volatility spillover increases from offshore to onshore markets, as discussed earlier, during the stress period. 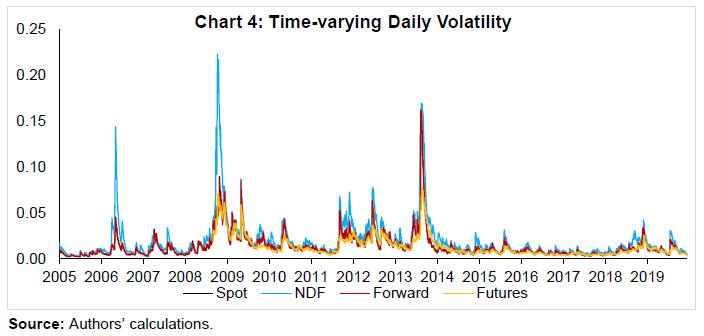 VII. Conclusion Since the work on establishing onshore-offshore price linkages in India was relatively sparse and inconclusive, the goal of this paper was to create an updated, empirical fact base, given the rapidity with which capital markets have developed and integrated, and the pace at which the NDF market has grown. The results for full sample present a stable long-run relationship between onshore and offshore markets with price discovery taking place in spot and forward markets. However, the direction of long-run causality reverses during the periods of stress (i.e., during April 2012 - November 2014 and October 2017 - December 2019) as found from sub-sample analysis. The long-run price spillover is observed to be mostly bidirectional between NDF and onshore futures markets though the causality is found from offshore to onshore during April 2012 to September 2017. For the full sample, the mean spillover (short-term spillover) is found to be bidirectional across onshore and offshore markets. That said, post the taper-tantrum (particularly, during November 2014 to December 2019), the short-term causality appears to have changed, from two-way to one-way, i.e., from offshore to onshore markets. Granger causality-in-mean tests further corroborate these findings. In view of the growing size of NDF market, these findings are cause of concern for policy-making, as any disruption in offshore market is beyond the domestic policy purview and can make domestic markets volatile. Results of volatility spillover analysis provide evidence of a unidirectional volatility spillover from spot and forward segments to NDF markets in normal circumstances which turns bidirectional in the presence of asymmetric effects. On the other hand, volatility transmission between futures market and NDF market is found to be bidirectional, with or without asymmetric responses. However, this feature of volatility spillovers has changed over time. The sub-sample analysis shows that volatility spillovers become unidirectional, from offshore to onshore, and increases significantly during the periods of heightened uncertainty (i.e., during April 2012 - November 2014 and October 2017 - December 2019). All told, as NDF volumes have increased in the recent period, they have begun to play an important role in both price discovery and driving volatility, particularly during heightened uncertainty period. Thus, a real-time basis monitoring of the market is essential to contain any significant spillovers from the offshore NDF market. Few policy measures undertaken by the Reserve Bank of India recently are likely to help in reducing rupee turnover in offshore centres and improve efficiency of price discovery. Some of these measures include the extension of trading hours, introduction of rupee derivatives at International Financial Services Centres (IFSC) and permitting Indian banks to participate in NDF market are likely to improve the access for overseas participants and curb turnover in offshore centres. Domestic banks participation in NDF segment would also support central bank at a time if it wants to intervene in offshore segment. The rise of NDF turnover in IFSC is expected to reduce the spread and thereby enhance the overall efficiency of the market.
References Bank for International Settlements (2019). Triennial Central Bank Survey of Foreign Exchange and Over-the-counter (OTC) Derivatives Markets in 2019. December, Basel. Behera, H. K. (2011). Onshore and offshore market for Indian rupee: recent evidence on volatility and shock spillover. Macroeconomics and Finance in Emerging Market Economies, 4(1), 43-55. Cadarajat, Y., & Lubis, A. (2012). Offshore and onshore IDR market: an evidence on information spillover. Bulletin of Monetary Economics and Banking, 14(4), 323-348. Caporale, G.M., Pittis, N. & Spagnolo, N. (2002). Testing for Causality-in-Variance: An Application to the East Asian Markets. International Journal of Finance and Economics, 7, 235-45. Cheung, Y.W. & Ng, L.K. (1996). A Causality in Variance Test and Its Application to Financial Market Prices. Journal of Econometrics, 72(1-2), 33-48. Coffey, N., Hrung, W.B. & Sarkar, A. (2009). Capital Constraints, Counterparty Risk, and Deviations from Covered Interest Rate Parity. Federal Reserve Bank of New York Staff Report, no. 393. Colavecchio, R., & Funke, M. (2008). Volatility transmissions between renminbi and Asia-Pacific on-shore and off-shore US dollar futures. China Economic Review, 19(4), 635-648. Darbha, G. (2012). A Tale of One Asset and Two Markets–Analysis of Dynamic Interactions between On-and Off Shore Markets. url: macrofinance.nipfp.org.in/PDF/13-11sl_Darbha_NDFNimrana.pdf. Debelle, G., Gyntelberg, J., & Plumb, M. (2006). Forward currency markets in Asia: lessons from the Australian experience. BIS Quarterly Review, 53-64, September. Ding, D.K., Tse, Y. & Williams, M.R. (2014). The price discovery puzzle in offshore yuan trading: different contributions for different contracts. The Journal of Futures Markets, 34(2), 103-123. Engle, R.F. & Kroner, K.F. (1995). Multivariate Simultaneous Generalized ARCH. Econometric Theory, 11, 122-50. Fung, H.-G., Leung, W.K., Zhu, J. (2004). Nondeliverable forward market for Chinese RMB: a first look. China Economic Review, 15, 348–352. Goyal, R., Jain, R., & Tewari, S. (2013). Non deliverable forward and onshore Indian rupee market: a study on inter-linkages. Reserve Bank of India Working Paper Series, No. 11, December. Gu, L., & McNelis, P. D. (2013). Yen/Dollar volatility and Chinese fear of floating: Pressures from the NDF market. Pacific-Basin Finance Journal, 22, 37-49. Guru, A. (2009). Non-Deliverable Forwards Market for Indian Rupee: An Empirical Study. Indian Journal of Economics and Business, 8(2), 245-260. Kroner, K. & Ng, V. (1998). Modelling Asymmetric Comovements of Asset Returns. The Review of Financial Studies, 11(4), 817-44. Kumar, A., & Rituraj (2020). Onshoring the Offshore. RBI Bulletin, August, 31-40. Kumar, U., & Jain, G. (2018). An Empirical Investigation on the Relationship between Onshore and Offshore Indian Rupee Market. Journal of Quantitative Methods, 2(1), 1-36. Ma, G., Ho, C., & McCauley, R. N. (2004). The markets for non-deliverable forwards in Asian currencies. BIS Quarterly Review, 81-94, June. Ma, G., & McCauley, R. N. (2013). Is China or India more financially open?. Journal of International Money and Finance, 39, 6-27. McCauley, R. N., & Shu, C. (2016). Non-deliverable forwards: impact of currency internationalisation and derivatives reform. BIS Quarterly Review, December, 81-93. ---- (2019). Recent renminbi policy and currency co-movements. Journal of International Money and Finance, 95, 444-456. Misra, S. & Behera, H. (2006), Non Deliverable Foreign Exchange Forward Market: An Overview. Reserve Bank of India Occasional Papers, 27, Winter, 25-55. Park, J. (2001). Information flows between non-deliverable forwards (NDF)/and spot markets: Evidence from Korean currency. Pacific Basin Finance Journal, 9, 363-377. Patel, N., & Xia, F. D. (2019). Offshore markets drive trading of emerging market currencies. BIS Quarterly Review, December, 53-67 Reserve Bank of India (2013). Annual Report 2012-13, August, 53-54. ---------(2019). Report of the Task Force on Offshore Rupee Markets, July, Mumbai. Saravanan, A., & Shanmugam, P.S. (2014). An empirical analysis of the interrelation between spot market & non-deliverable forward market of USD/INR in the pre- and post-currency futures era. Elk Asia Pacific Journal of Finance and Risk Management, 5, 1-22. Schmittmann, J.M. and C.H. Teng (2020). Offshore Currency Markets: Non-Deliverable Forwards (NDFs) in Asia, IMF Working Paper No. 20/179. Su, C., Wang, K., Zhang, H. & Nian, R. (2019). Can onshore spot market progress influence offshore N.D.F. market development for the C.N.Y? Economic Research-Ekonomska Istraživanja, 32(1), 1621-1644. Wang, K., Fawson, C. & Chen, M. (2007). Information Flows among Exchange Rate Markets: What Do We Learn From Non-Deliverable Forward Markets in Asia?. Chaoyang University of Technology, October, url: http://www.cyut.edu.tw/~finance/docs/1030-2.pdf. Wooldridge, P. (2019). FX and OTC Derivatives markets through the lens of the Triennial Survey. BIS Quarterly Review, December, 15-19.
Appendix | Table A.1: Bai-Perron Structural Break Test Result | | | Coefficient | t-stat | P-value | | No. of Observations = 963 Intercept | -3.76*** | -72.20 | 0.00 | | No. of Observations = 943 Intercept | -3.86*** | -105.73 | 0.00 | | No. of Observations = 668 Intercept | -4.06*** | -114.72 | 0.00 | | No. of Observations = 752 Intercept | -4.18*** | -314.87 | 0.00 | | No. of Observations = 586 Intercept | -4.23*** | -139.52 | 0.00 | Note: Break Dates: September 8, 2008; April 23, 2012; November 11, 2014; September 30, 2017;
***: Significant at 1 per cent level.
Source: Authors’ estimation. |
| Table A.2: MGARCH-BEKK Parameter Estimates - Spot and NDF | | Variable | Sub-Sample 1 | Sub-Sample 2 | Sub-Sample 3 | Sub-Sample 4 | Sub-Sample 5 | | Coeff | P-value | Coeff | P-value | Coeff | P-value | Coeff | P-value | Coeff | P-value | | Mean Equation | | ∆On(-1) | -0.16 | 0.00 | -0.30 | 0.00 | -0.41 | 0.00 | -0.38 | 0.00 | -0.29 | 0.00 | | ∆On(-2) | -0.02 | 0.66 | -0.19 | 0.00 | -0.37 | 0.00 | | | -0.18 | 0.02 | | ∆On(-3) | -0.06 | 0.17 | -0.03 | 0.59 | -0.06 | 0.27 | | | | | | ∆Off(-1) | 0.13 | 0.00 | 0.30 | 0.00 | 0.39 | 0.00 | 0.39 | 0.00 | 0.28 | 0.01 | | ∆Off(-2) | 0.06 | 0.09 | 0.21 | 0.00 | 0.25 | 0.00 | | | 0.13 | 0.09 | | ∆Off(-3) | 0.04 | 0.23 | 0.01 | 0.85 | 0.06 | 0.28 | | | | | | Constant | -0.02 | 0.58 | 0.46 | 0.01 | 0.26 | 0.00 | -0.10 | 0.12 | 0.08 | 0.01 | | ecm_on(-1) | -0.01 | 0.59 | -0.15 | 0.01 | -0.20 | 0.00 | -0.13 | 0.11 | -0.28 | 0.01 | | ∆On(-1) | 0.30 | 0.00 | 0.16 | 0.05 | 0.04 | 0.58 | -0.08 | 0.37 | 0.10 | 0.41 | | ∆On(-2) | 0.23 | 0.00 | 0.10 | 0.18 | -0.10 | 0.21 | | | -0.02 | 0.85 | | ∆On(-3) | 0.00 | 0.99 | 0.16 | 0.01 | -0.02 | 0.75 | | | | | | ∆Off(-1) | -0.22 | 0.00 | -0.12 | 0.13 | -0.03 | 0.65 | 0.13 | 0.15 | -0.10 | 0.37 | | ∆Off(-2) | -0.17 | 0.00 | -0.07 | 0.33 | 0.01 | 0.86 | | | -0.05 | 0.60 | | ∆Off(-3) | -0.07 | 0.07 | -0.16 | 0.01 | -0.01 | 0.86 | | | | | | Constant | 0.23 | 0.00 | -0.26 | 0.21 | -0.20 | 0.01 | 0.14 | 0.06 | -0.03 | 0.44 | | ecm_off(-1) | 0.15 | 0.00 | 0.08 | 0.21 | 0.16 | 0.01 | 0.17 | 0.06 | 0.11 | 0.42 | | Variance Equation | | C(1,1) | 0.02 | 0.00 | 0.03 | 0.00 | 0.03 | 0.00 | 0.04 | 0.00 | 0.02 | 0.02 | | C(2,1) | 0.02 | 0.00 | 0.03 | 0.00 | 0.02 | 0.01 | 0.05 | 0.00 | 0.02 | 0.00 | | C(2,2) | 0.00 | 0.59 | 0.00 | 1.00 | 0.00 | 0.57 | 0.00 | 1.00 | 0.01 | 0.01 | | A(1,1) | 0.26 | 0.00 | 0.37 | 0.00 | 0.19 | 0.04 | 0.30 | 0.01 | 0.47 | 0.01 | | A(1,2) | -0.16 | 0.00 | 0.19 | 0.01 | -0.05 | 0.59 | 0.19 | 0.16 | 0.19 | 0.36 | | A(2,1) | 0.13 | 0.00 | -0.31 | 0.00 | 0.13 | 0.05 | 0.05 | 0.59 | -0.32 | 0.02 | | A(2,2) | 0.57 | 0.00 | -0.06 | 0.47 | 0.26 | 0.00 | 0.26 | 0.03 | 0.02 | 0.91 | | B(1,1) | 0.92 | 0.00 | 0.70 | 0.00 | 0.90 | 0.00 | 0.89 | 0.00 | 0.77 | 0.00 | | B(1,2) | -0.01 | 0.84 | -0.32 | 0.00 | 0.01 | 0.82 | -0.09 | 0.34 | -0.17 | 0.15 | | B(2,1) | -0.02 | 0.32 | 0.25 | 0.00 | 0.01 | 0.67 | -0.13 | 0.12 | 0.16 | 0.03 | | B(2,2) | 0.85 | 0.00 | 1.20 | 0.00 | 0.96 | 0.00 | 0.81 | 0.00 | 1.07 | 0.00 | | D(1,1) | -0.15 | 0.06 | 0.03 | 0.76 | 0.11 | 0.44 | 0.01 | 0.96 | 0.09 | 0.80 | | D(1,2) | -0.30 | 0.00 | -0.08 | 0.38 | -0.17 | 0.24 | -0.04 | 0.88 | 0.09 | 0.87 | | D(2,1) | 0.19 | 0.00 | 0.13 | 0.20 | -0.07 | 0.44 | -0.09 | 0.59 | 0.12 | 0.67 | | D(2,2) | 0.08 | 0.46 | 0.21 | 0.03 | 0.14 | 0.19 | -0.02 | 0.93 | 0.12 | 0.81 | | No. of Obs. | 959 | | 939 | | 664 | | 750 | | 583 | | | Log-likelihood | 2410 | | 1602 | | 1212 | | 2485 | | 1702 | | | MV-Q (8) | 36.7 | 0.26 | 24.6 | 0.82 | 31.0 | 0.52 | 69.1 | 0.57 | 37.1 | 0.24 | Note: MV-Q refers to multivariate Q test of the standardised residuals for ARCH effects up to lag 8.
Source: Authors’ calculations |
| Table A.3: MGARCH-BEKK Parameter Estimates - Forward and NDF | | Variable | Sub-Sample 1 | Sub-Sample 2 | Sub-Sample 3 | Sub-Sample 4 | Sub-Sample 5 | | Coeff | P-value | Coeff | P-value | Coeff | P-value | Coeff | P-value | Coeff | P-value | | Mean Equation | | ∆On(-1) | -0.19 | 0.00 | -0.30 | 0.00 | -0.38 | 0.00 | -0.30 | 0.00 | -0.32 | 0.00 | | ∆On(-2) | -0.05 | 0.32 | -0.22 | 0.00 | -0.36 | 0.00 | | | -0.23 | 0.00 | | ∆On(-3) | -0.06 | 0.17 | -0.05 | 0.10 | -0.09 | 0.16 | | | | | | ∆Off(-1) | 0.13 | 0.00 | 0.29 | 0.00 | 0.36 | 0.00 | 0.28 | 0.00 | 0.30 | 0.00 | | ∆Off(-2) | 0.09 | 0.03 | 0.22 | 0.00 | 0.23 | 0.00 | | | 0.18 | 0.02 | | ∆Off(-3) | 0.04 | 0.25 | 0.06 | 0.05 | 0.05 | 0.38 | | | | | | Constant | -0.06 | 0.28 | 0.45 | 0.02 | 0.09 | 0.00 | 0.35 | 0.00 | 0.25 | 0.00 | | ecm_on(-1) | -0.04 | 0.29 | -0.18 | 0.02 | -0.23 | 0.00 | -0.34 | 0.00 | -0.46 | 0.00 | | ∆On(-1) | 0.31 | 0.00 | 0.03 | 0.59 | 0.03 | 0.76 | -0.07 | 0.48 | -0.05 | 0.68 | | ∆On(-2) | 0.24 | 0.00 | 0.02 | 0.79 | -0.13 | 0.19 | | | -0.14 | 0.13 | | ∆On(-3) | 0.02 | 0.70 | 0.09 | 0.00 | -0.05 | 0.52 | | | | | | ∆Off(-1) | -0.21 | 0.00 | -0.01 | 0.86 | -0.02 | 0.82 | 0.10 | 0.31 | 0.02 | 0.85 | | ∆Off(-2) | -0.15 | 0.00 | 0.00 | 0.95 | 0.03 | 0.72 | | | 0.07 | 0.46 | | ∆Off(-3) | -0.06 | 0.11 | -0.07 | 0.01 | 0.00 | 0.96 | | | | | | Constant | 0.26 | 0.00 | -0.71 | 0.00 | -0.08 | 0.05 | -0.16 | 0.15 | -0.05 | 0.55 | | ecm_off(-1) | 0.18 | 0.00 | 0.28 | 0.00 | 0.19 | 0.04 | 0.16 | 0.15 | 0.09 | 0.52 | | Variance Equation | | C(1,1) | 0.02 | 0.00 | 0.11 | 0.00 | 0.03 | 0.00 | 0.05 | 0.00 | 0.02 | 0.00 | | C(2,1) | 0.02 | 0.00 | 0.10 | 0.00 | 0.02 | 0.00 | 0.05 | 0.00 | 0.02 | 0.01 | | C(2,2) | 0.01 | 0.06 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.01 | 0.00 | | A(1,1) | 0.30 | 0.00 | 0.69 | 0.00 | 0.13 | 0.13 | 0.27 | 0.03 | -0.52 | 0.00 | | A(1,2) | -0.14 | 0.01 | 0.35 | 0.00 | -0.09 | 0.26 | 0.19 | 0.21 | -0.87 | 0.00 | | A(2,1) | 0.11 | 0.02 | -0.29 | 0.00 | 0.18 | 0.01 | 0.13 | 0.23 | 0.25 | 0.04 | | A(2,2) | 0.57 | 0.00 | 0.02 | 0.76 | 0.29 | 0.00 | 0.33 | 0.01 | 0.62 | 0.00 | | B(1,1) | 0.90 | 0.00 | -0.85 | 0.02 | 0.91 | 0.00 | 0.89 | 0.00 | 1.00 | 0.00 | | B(1,2) | -0.03 | 0.39 | -1.52 | 0.00 | 0.01 | 0.66 | -0.10 | 0.47 | 0.12 | 0.11 | | B(2,1) | 0.00 | 0.94 | 0.43 | 0.01 | 0.00 | 0.92 | -0.22 | 0.08 | -0.07 | 0.21 | | B(2,2) | 0.86 | 0.00 | 1.31 | 0.00 | 0.95 | 0.00 | 0.71 | 0.00 | 0.83 | 0.00 | | D(1,1) | -0.20 | 0.01 | 0.67 | 0.00 | 0.11 | 0.43 | 0.00 | 1.00 | 0.35 | 0.08 | | D(1,2) | -0.28 | 0.00 | 0.67 | 0.00 | -0.14 | 0.33 | 0.00 | 1.00 | 0.33 | 0.15 | | D(2,1) | 0.26 | 0.00 | -0.67 | 0.00 | -0.07 | 0.45 | 0.00 | 1.00 | -0.38 | 0.00 | | D(2,2) | 0.10 | 0.29 | -0.63 | 0.00 | 0.12 | 0.25 | 0.00 | 1.00 | -0.36 | 0.03 | | No. of Obs. | 959 | | 939 | | 664 | | 750 | | 583 | | | Log-lik. | 2437 | | 1601 | | 1215 | | 2533 | | 1736 | | | MV-Q (8) | 37.4 | 0.23 | 32.7 | 0.43 | 32.6 | 0.44 | 55.6 | 0.92 | 33.3 | 0.41 | Note: MV-Q refers to multivariate Q test of the standardised residuals for ARCH effects up to lag 8.
Source: Authors’ calculations. |
| Table A.4: MGARCH-BEKK Parameter Estimates - Futures and NDF | | Variable | Sub-Sample 2 | Sub-Sample 3 | Sub-Sample 4 | Sub-Sample 5 | | Coeff | P-value | Coeff | P-value | Coeff | P-value | Coeff | P-value | | Mean Equation | | ∆On(-1) | -0.32 | 0.00 | -0.21 | 0.00 | -0.19 | 0.00 | -0.20 | 0.00 | | ∆On(-2) | -0.17 | 0.00 | -0.15 | 0.02 | | | -0.16 | 0.00 | | ∆On(-3) | 0.01 | 0.87 | -0.03 | 0.51 | | | | | | ∆Off(-1) | 0.33 | 0.00 | 0.28 | 0.00 | 0.17 | 0.00 | 0.17 | 0.01 | | ∆Off(-2) | 0.18 | 0.00 | 0.07 | 0.29 | | | 0.15 | 0.01 | | ∆Off(-3) | 0.01 | 0.84 | 0.01 | 0.89 | | | | | | Constant | 0.48 | 0.00 | 0.33 | 0.00 | 0.22 | 0.00 | 0.15 | 0.00 | | ecm_on(-1) | -0.26 | 0.00 | -0.40 | 0.00 | -0.44 | 0.00 | -0.43 | 0.00 | | ∆On(-1) | -0.08 | 0.26 | 0.18 | 0.04 | -0.02 | 0.69 | 0.00 | 0.97 | | ∆On(-2) | -0.09 | 0.20 | 0.04 | 0.60 | | | -0.09 | 0.21 | | ∆On(-3) | 0.04 | 0.47 | -0.06 | 0.30 | | | | | | ∆Off(-1) | 0.10 | 0.09 | -0.12 | 0.15 | 0.00 | 0.94 | -0.04 | 0.64 | | ∆Off(-2) | 0.12 | 0.05 | -0.10 | 0.23 | | | -0.01 | 0.93 | | ∆Off(-3) | 0.00 | 0.93 | -0.01 | 0.93 | | | | | | Constant | -0.32 | 0.01 | -0.03 | 0.64 | -0.01 | 0.80 | -0.02 | 0.45 | | ecm_off(-1) | 0.17 | 0.01 | 0.04 | 0.62 | 0.02 | 0.73 | 0.07 | 0.42 | | Variance Equation | | C(1,1) | 0.02 | 0.00 | 0.01 | 0.07 | 0.03 | 0.00 | 0.02 | 0.05 | | C(2,1) | 0.01 | 0.20 | -0.01 | 0.13 | 0.05 | 0.00 | -0.01 | 0.64 | | C(2,2) | 0.01 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | -0.01 | 0.43 | | A(1,1) | 0.24 | 0.00 | -0.06 | 0.27 | -0.03 | 0.67 | -0.04 | 0.66 | | A(1,2) | 0.04 | 0.47 | -0.15 | 0.05 | -0.05 | 0.67 | -0.44 | 0.00 | | A(2,1) | -0.11 | 0.01 | 0.29 | 0.00 | 0.27 | 0.00 | -0.09 | 0.23 | | A(2,2) | 0.18 | 0.00 | 0.25 | 0.00 | 0.51 | 0.00 | 0.43 | 0.00 | | B(1,1) | 0.92 | 0.00 | 1.11 | 0.00 | 0.80 | 0.00 | 0.64 | 0.00 | | B(1,2) | 0.01 | 0.57 | 0.36 | 0.00 | -0.27 | 0.11 | -0.11 | 0.20 | | B(2,1) | 0.05 | 0.01 | -0.18 | 0.00 | -0.02 | 0.84 | 0.29 | 0.00 | | B(2,2) | 0.96 | 0.00 | 0.72 | 0.00 | 0.72 | 0.00 | 1.02 | 0.00 | | D(1,1) | 0.19 | 0.01 | -0.09 | 0.36 | 0.55 | 0.00 | 0.20 | 0.48 | | D(1,2) | 0.01 | 0.91 | -0.44 | 0.00 | 0.43 | 0.02 | -0.02 | 0.92 | | D(2,1) | 0.02 | 0.73 | 0.07 | 0.42 | -0.23 | 0.01 | -0.29 | 0.08 | | D(2,2) | 0.03 | 0.63 | 0.23 | 0.02 | 0.02 | 0.90 | -0.14 | 0.31 | | No. of Obs. | 939 | | 664 | | 750 | | 583 | | | Log-lik. | 1568 | | 1152 | | 2061 | | 1525 | | | MV-Q (8) | 18.9 | 0.97 | 21.8 | 0.91 | 91.5 | 0.06 | 27.1 | 0.71 | Note: MV-Q refers to multivariate Q test of the standardised residuals for ARCH effects up to lag 8.
Source: Authors’ calculations. | |