Sunil Kumar*
This paper attempts to identify determinants of real exchange rate in India. Apart from providing theoretical background on possible determinants of real exchange rate, the paper tests their statistical significance using autoregressive distributed lag (ARDL) modelling approach. It finds that among the identified variables chosen a priori based on theoretical arguments as determinants of RER, productivity differential, external openness, terms of trade and net foreign assets turn out to be statistically significant. The signs of the short-run dynamic impact have been found consistent with long-run coefficients and error correction term is negative and statistically significant implying convergence to long-run equilibrium path. Since the fitted RER is found to be quite closer to the actual behavior exhibited by RER, the variables identified with certain lags could, therefore, serve as lead indicators of real exchange rate behaviour. On the basis of results, it may be noted that appreciation in RER should not always be seen as decline in international competitiveness of the traded sector as some of the factors contributing to the RER appreciation are attributed to higher growth reflecting improvement in competitiveness.
JEL Classification : E31, F31, C15.
Keywords : Real Exchange Rate, Economic Growth, Balassa-Samuelson hypothesis, Autoregressive Distributed Lag
Introduction
Real exchange rate (RER) is considered as barometer of the competitiveness of an economy for international trade. The higher real exchange rate ceteris paribus entails country’s exports more expensive and imports relatively cheaper. Thus, affecting the prices of exports and imports, RER movements result in to variation in the allocation of internal production and consumption between traded and non-traded goods. RER assumes utmost importance in developing countries where non-tradable goods constitute a large segment of the goods market and only their prices are flexible as prices of traded goods are largely determined in world market. Therefore, the volatility in the prices of non-traded goods leads to misalignment of RER from its equilibrium level and supposedly, affects adversely the competitiveness and economic growth. In fact, recurrent and large misalignments are linked to lower growth rates and current account deficits in the long run and very frequently with currency and financial crisis. However, it has been debated for some times whether devaluations in RER are contractionary or expansionary. On the one hand, in the conventional textbook model, assuming the Marshall- Lerner condition holds, devaluations are supposed to increase competitiveness, increase production and exports of tradable goods, reduce imports, and thereby improve trade balance, GDP and employment. On the other hand, evidence from many countries reveals that currency appreciation results from accelerated economic development, whereas reverse is true in case of deceleration in economic development. Balassa-Samuelson hypothesis (1963), one of the most important hypotheses with respect to the equilibrium real exchange rate level, postulates that rapid economic growth is accompanied by real exchange rate appreciation because of differential productivity growth between tradable and non-tradable sectors. However, the analysis of the relationship between the level of economic development and real exchange rate, as was suggested by the seminal paper of Balassa-Samuelson, do not find much of the place in the history of research. Nevertheless, open economy macroeconomics has provided with a framework on equilibrium exchange rate level compatible with overall economic equilibrium, as well as policy instruments necessary to correct the possible misalignment.
The findings of various studies on the impact of real exchange rate on economic activities also differ distinctly. Aguirre and Calderon (2005) has found that large overvaluations and undervaluation in RER hurt growth, whereas small undervaluation can boost growth. On the other hand, Diaz-Alejandro (1963), Krugman and Taylor (1978), and Lizondo and Montiel (1989) have found that expansionary effect of real devaluations in tradable sector could be offset by contractionary impact in the non-tradable sector. Edwards (1989) investigated the relationship between real exchange rate misalignment and economic performances and concludes that real exchange rate difference with regards to its equilibrium level has a negative effect. Cottietal (1990) confirms that for some Latin American countries real exchange rate instability has handicapped exportation growth, whereas Asian exportation growth has been for the most part accounted for by real exchange rate stability. According to Sekkat and Varoudakis (1998), the chronic misalignments of real exchange rate are a major factor of the weak economic performances of developing countries. Ghura and Grennes (1993) show on a panel of African countries that real exchange rate misalignment negatively affected economic growth, exports, investment and saving.
Even though, it is not very clear whether net impact of RER devaluations is positive or negative in an economy, several emerging market and developing economies have resisted devaluation in the last many years partly because of concerns that such policy would be contractionary. This view arises from the experience of countries such as Mexico, where real depreciations (increase) of the Peso have consistently been associated with declines in output, while real appreciations (decrease) have been linked to expansion (Villavicencio and Bara, 2006). Furthermore, real exchange rate stability and alignments have assumed critical importance in policy formulations particularly in EMEs to improve economic performance during recent years. Real exchange rate misalignment affects economic activity in developing countries mainly due to their dependence on imported capital goods and specialization in commodity exports. Evidence from developing countries is often quoted to support the view that the link between RER misalignment and economic performance is strong.
Given the fact that RER movements and economic growth have got some association positive or negative, the determinants of RER becomes more relevant from policy perspective. In fact, a number of researchers have also pointed out the importance of understanding the main determinants of real exchange rate (Edwards, 1989; Elbadawi
and Soto, 1997; Ebadawi, 1994; and Ghura and Grennes, 1993).
Furthermore, this is well established that in most of the cases, especially in emerging market and developing economies, RER does not strictly converge to purchasing power parity (PPP) and even if it does in some cases in the long-run, the rate of convergence remains very slow resulting from underlying macroeconomic fundamentals. This implies that impulse response of RER to movements in macroeconomic fundamentals is very pronounced.
Therefore, the objective of this paper is to identify theoretically the determinants of RER and empirically investigate the link between RER and select determinants in case of India. The structure of the remainder of the paper is as follows. The theoretical framework and macroeconomic variables as determinants of RER has been given in section II, while Section III dwells upon the RER evolution in India. Section IV provides details on sources of data and research methodology. Empirical results have been discussed in section V. The concluding observations have been furnished in section VI.
Section II
Theoretical Framework and Determinants
Theoretical framework
In order to specify the nature of the relation to be tested through econometrics techniques, the Balassa-Samuelson hypothesis has been taken as minimal theoretical framework for real exchange rate determination. For this purpose, a small open economy is considered, which is composed of a set of homogeneous firms. The representative firm produces two goods: a tradable commodity for the world market and a non-tradable one for domestic demand. The tradable goods production is presumed to require both capital and labour, while nontradable goods production uses only labour. The competition is supposed to be perfect and it ensures that production factors are paid at their marginal productivity and at the same time, labour factor mobility ensures equal pay. Whereas labour supply is supposed to be
constant and all variables are expressed in terms of tradable goods.
In this study, an extension of the benchmark model is used where the equilibrium real exchange rate is a path upon which an economy maintains both internal and external balances. The equilibrium real exchange rate depends not only on productivities but also on some other real variables. This model used in the present study is basically developed by Montiel (cited by Mkenda 2001). Real exchange rate is
defined as the relative price of traded and non-traded goods. That is :
 Where, PT is the world price for traded goods and PN is the price of non-traded ones. This definition is called internal real exchange rate and is appropriate for developing countries where exports are predominately primary products and law of one price holds. The law of one price entails that price of traded goods is equivalent across the countries in common currency. Edwards (1989) mentions that this definition provides a consistent index of the country’s tradable sector competitiveness and also influences resources allocation as an increase in q would cause a shift of resources away from the traded to the non traded sector. As per definition (1), the dynamics of the internal relative price of non tradable goods drives the movements in RER as law of one prices holds in case of traded goods and their prices amount equivalent to world prices, especially in emerging market and developing economies.
The definition of real exchange rate could be generalized and written in log form as follows.
Where, p and p* are respectively the national and foreign price indices, and assuming that log p and log p* can be split into traded and non traded prices as below.
So, substituting (3) and (4), definition (2) could be rewritten as:
Under the hypothesis that the law of one price is valid for traded goods and foreign prices of traded and non traded goods, (log p*N – log p*T), are given, the first term in equation (5) vanishes and real exchange rate varies only with the domestic relative price of non traded goods. After establishing the validity of prices of non traded goods as the driver of real exchange rate, next step would be to find out the macroeconomic variables, which causes variations in prices of non traded goods. These macroeconomic variables could be identified as determinants of real exchange rate.
Considering the RER framework detailed in equations (1 to 5), wherein it has been derived that RER is primarily the function of prices of non traded goods and the equilibrium RER is determined by a set of macroeconomic variables (fundaments), the same can be estimated using suitable econometric techniques. For estimation, the relationship between equilibrium RER and fundaments could be defined in the following single equation :
Where Xt are the macroeconomic fundamentals, β the vector of long run coefficients and εt an error term. Clark and MacDonalds (1999) suggests that sustainable or permanent component of fundamentals can be used to construct the equilibrium RER path. Thus, the equilibrium RER path can be obtained estimating equation (6) as under :
  RER stability and its correct alignment are known to be necessary conditions - though not sufficient - for economic development (Williamson, 1997). Considering this argument, numerous studies have been undertaken for estimations of equilibrium real exchange rates in developing countries during the eighties and early nineties. These studies on real exchange rate try to find the determinants of RER and then estimate its long run level. Indeed, once this has been done, one can determine the necessary adjustments to reach equilibrium. Moreover, equilibrium real exchange rate determinants identification enables to forecast its evolution and then to choose the appropriate measures to remedy possible differences and to determine the necessary adjustments with regards to economic policy purposes.
Determinants
The equilibrium real exchange rate is defined as the relative price of non-traded to traded goods compatible with simultaneous attainment of the internal and external equilibrium (Edwards, 1989). Internal equilibrium entails clearing of non traded goods and labour markets; while in case of external equilibrium the intertemporal budget constraint is applicable i.e. the economy is intertemporal solvent. Edwards and Savastano (1999) mention that the equilibrium real exchange rate is driven by a set of foreign and domestic real variables called fundamentals in the long run. In theoretical models, the equilibrium real exchange rate is generally linked to government spending, productivity differential (the Balassa-Samuelson effect), terms of trade, external openness of the economy, foreign capital inflows, and net foreign assets, among other variables. According to Edwards (1989), both real and nominal variables affect equilibrium real exchange rate, where as it respond only to fundamentals in the long run. In view of above, the real exchange rate movements may be endogenously generated by variations in fundamentals and hence, not necessarily means disequilibrium situations.
The studies by Ghura and Grennes (1993), Aron et al (1997), Cottietal (1990) and Elbadawi and Soto (1997) find that real exchange rate determinants are mainly the terms of trade, the openness degree of the economy, imports and capital flows.
We have considered the determinants of RER in India on the basis of extant theoretical literature and numerous empirical studies undertaken in respect of other countries having somewhat similar economic structure. The Edwards model (1988), a theoretical framework for equilibrium RER used in various empirical studies on developing and EMEs, has been used in the present study. The macroeconomic fundaments, considered as possible determinants of RER in case of India, are productivity differential, government spending, terms of trade (TOT), external openness, capital flows and net foreign assets. The justification for choosing these macroeconomic fundamentals as possible determinants of RER has been discussed below:
a. Productivity Differentials : The productivity differential impact refers to the Balassa-Samuelson model (Balassa, 1964; Samuelson, 1964). Balassa-Samuelson hypothesis presents that in an open economy, which is divided into two sectors i.e. traded and non-traded, the relative price of non-traded goods to traded goods influence the real exchange rate to large extent and productivity differentials in these sectors are reflected in their relative price movements. When traded sector experience large productivity gains, the wage rates in this sector moves upward commensurately, but at the same time, wage rates in non-traded sector also increase equally, albeit productivity rise remains significantly lower. Since wage increase in traded goods sector is matched by productivity improvement, the prices of traded goods do not rise. Moreover, if it is small open economy, the price of traded goods are exogenously given. On the contrary, in the nontraded goods sector, acceleration in wage rates is more than productivity escalation and this difference leads to increase in the price. In this example, productivity differential eventually result to increase in price of non-traded goods in a small open economy, which in turn leads to an increase in the relative price of nontraded goods. So, productivity differential in traded and nontraded sectors causes rise in the price level of an open economy and appreciation of the home country’s real exchange rate.
Assuming a Cobb Douglas production function with constant returns to scale in both sectors, the formal the Balassa-Samuelson effect could be expressed as under :
Where, a hat above a variable denotes growth rate. Thus, as per equation 11, the real exchange rate depends entirely on productivity differentials. Moreover, the Balassa-Samuelson effect can also be interpreted as the effect of the economic development on real exchange rate, i.e. the real exchange rate tends to appreciate in the fast growing countries as these economies witness large productivity gains and that get reflected in rise in general price level through upward movement in the prices of non-traded goods.
b. Capital Flows and Net Foreign Assets : BS hypothesis revolves around the core principle of international trade. And, until recently, the appreciation of the real exchange rate in emerging and developing countries was attributed to the BS effect through increase in the relative prices of non-traded goods. The collapse of Bretton Woods system in early 1970s and heightened volatilities in foreign exchange markets across the world paved the way for capital flows. A large number of emerging and developing countries also introduced economic reforms comprising of macroeconomic stabililisation i.e. containing inflation, fiscal deficit and external debt and structural changes i.e. developing and strengthening money and financial markets, globalization (enhancing external openness through trade and financial flows), liberalization/ privatization etc. As a result, economic landscape underwent a transformation with increasing financial flows across the countries following increasingly integration of international financial markets during 1990s and 21st century.
Alongside increasing international financial markets integration, it was debated that besides productivity differential, there is something else also which explains the recurrent deviations in exchange rate from its PPP level and jury was out with capital flows as one of the crucial factors behind the movements in exchange rate. Therefore, it is broadly accepted that trade and capital flows influence the exchange rate. A surge in capital flows leads to an increase in consumption demand for both traded and non-traded goods. In case of non-traded goods, excess demand generated by capital flows is not proportionately matched with rise in supply and hence, result into rise in the price of non-traded goods to reach to equilibrium. On the other hand, elevated demand for traded goods is met with imported goods without any affect on the price reflecting law of one price (LOP) and this leads to widening trade deficit. Accordingly, increase in the relative price of non-traded goods would entails an appreciation of the real exchange rate.
Generally, a country’s current account balance is matched with net capital flows. If, current account is in deficit (surplus), then there would be net capital inflows (outflows). However, there could also be a situation when net capital inflows are more (less) than current account deficit and lead to accretion (erosion) of net foreign assets of the country. Thus, net foreign assets tend to influence a country’s exchange rate and that is why, foreign exchange balance is commonly used as one of the determinants of real exchange rate. Lane and Milessi-Ferreti (1999) investigate the theoretical relationship between the real exchange rate and net foreign assets and finds that the net foreign assets as an important determinant of the real exchange rate for developing and developed countries.
Net foreign assets influence the real exchange rate through various channels. The portfolio-balances considerations suggest that a deficit in the current account creates an increase in the net foreign debt of a country, which has to be financed by international investors and they demand for a higher yield to adjust their portfolio (Antonia and Bara, 2006). At given interest rate, this can only be achieved through a depreciation of the currency of the debtor country. Furthermore, the servicing of external debt accumulated through funding current account deficit entails a country to generate addition foreign exchange through promoting exports of goods and services. Therefore, the country needs to depreciate its currency to increase competitiveness of its exports (balance of payments channel also requires that (Maeso- Fernandez, et al (2001)).
In sum, rising current account deficit would be financed with an increase in capital flows and excess capital flows would lead to appreciation in real exchange rate. In the process, either excess capital flows would result in appreciation of nominal exchange rate or rise in prices with increasing money supply in the system. It may be noted that if a country relies on foreign capital for high levels of domestic absorptions (investment), RER is bound to appreciate regardless of the exchange rate regime in vogue. Thus, the real exchange rate is expected to appreciate (depreciate) with rise (fall) in foreign assets of a country. Like other emerging and developing countries, capital flows are susceptible to influence the movement in real exchange rate in India1.
c. Government Spending: The Balassa-Samuelson model presumes that real exchange rate is supply side phenomenon, means demand factors do not have any impact on the real exchange rate. BS model also assumes certain conditions in vogue viz., prefect competition in goods market, free factors mobility between two sectors of production, international capital mobility, law of one price and constant returns to scale in both trade and non-traded sectors (Froot and Rogoff (1995) and De Gregorio et al. (1994)). However, in practice, all these conditions are difficult to be in existence especially in emerging and developing countries. Jorge and Restout (2008) mention that demand factors can have an effect on the relative price of nontraded goods if one of the above conditions is relaxed. In this regard, Aguirre and Calderon (2005) introduce monopolistic competition in the non-traded sector in Lane and Milesi-Ferretti’s (2004) model and consider demand factors to determine the real exchange rate. Institutively, it is believed that the government expenditure is disproportionately incurred on non-traded goods, which leads to upward pressure on relative price of non-traded goods and appreciation in exchange rate. Otherwise also, generally higher government expenditure tends to be inflationary as it pushes the aggregate demand upward and supply response is not contemporaneous.
d. Terms of Trade: Terms of trade (ToT) affect the real exchange rate through income effect and substitution affect and net affect depends on the relative strength of these affects as both effects work in reverse direction to each other. Therefore, theoretical models although provide the importance of ToT disturbances as potential source of real exchange rate fluctuations, their impact on the real exchange rate remains undefined. On the one hand, deterioration in ToT generates negative income effect through decline in the domestic purchasing power and adversely affects the private demand for non-traded goods and leads to decline in prices eventually resulting into real depreciation of the exchange rate. On the other hand, weakening ToT induces substitution effect and makes the consumption of imported goods more expensive. The substitution effect result into shift of demand in favour of non-traded goods increasing their prices and real appreciation in exchange rate. As mentioned above, the total effect of a ToT worsening on real exchange rate would depend on the strength of the income and substitution effects. However, recent empirical studies have found that the income effect is predominant; hence, ToT improvements are associated with real appreciation in the long-run.
e. External openness: The extent of external openness of an economy influences the movement in real exchange rate in many ways. Firstly, increase in external openness through reduction in tariffs makes imports cheaper and shift the demand away from non-traded goods towards imported goods. The prices of nontraded goods decline and real exchange rate depreciates in this process to ensure equilibrium in non-traded goods segment. The second influence channel of external openness on real exchange rate has been provided in the model by Obstfeld and Rogoff (2002). As per their model, there exist a negative relationship between external openness and real exchange rate volatility. Basic tenet of their model is that monopoly/ monopolistic competition like market conditions prevail in non-traded goods segment and hence, promote the aggregate price rigidity. While traded goods allow the convergence of the domestic price indices. Because of aggregate price rigidity, a larger real exchange rate changes would be needed for a relatively closed economy to ensure equilibrium in domestic market. Hau (2002) mentions that more open countries behave more like flexible prices economies with smaller real exchange rate fluctuations since more imported goods provide a channel for quick adjustment of the national price indices. Using a panel of forty eight countries, Hau provids evidence of the negative relationship between real exchange rate volatility and trade openness. So, it is amply clear that increasing external sector openness leads to lower volatility as well as depreciation in real exchange rate.
Section III
Evolution of Real Exchange Rate in India
The evolution of India’s real exchange rate may be viewed in line with the shifts in India’s exchange rate policies over the last few decades from a par value system to a basket-peg and further to a managed float exchange rate system. During the period from 1947 to 1971, India followed the par value system of exchange rate. Initially, the rupee’s external par value was fixed at 4.15 grains of fine gold. The Reserve Bank maintained the par value of the rupee within the permitted margin of ±1 per cent using pound sterling as the intervention currency. Since the sterling-dollar exchange rate was kept stable by the US monetary authority, the exchange rates of rupee in terms of gold as well as the dollar and other currencies were indirectly kept stable. The devaluation of rupee in September 1949 and June 1966 in terms of gold resulted in the reduction of the par value of rupee in terms of gold to 2.88 and 1.83 grains of fine gold, respectively. The exchange rate of the rupee remained unchanged between 1966 and 1971. Therefore, evolution of real exchange rate during this period was guided mainly by the changes in prices in India as well as its trading partners.
With the breakdown of the Bretton Woods System in 1971 and the floatation of major currencies, the rupee was also linked with pound sterling in December 1971. Since sterling was fixed in terms of US dollar under the Smithsonian Agreement of 1971, the rupee also remained stable against dollar. In order to overcome the weaknesses associated with a single currency peg and to ensure stability of the exchange rate, the rupee, with effect from September 1975, was pegged to a basket of currencies. The currency selection and weights assigned were left to the discretion of the Reserve Bank. The currencies included in the basket as well as their relative weights were kept confidential in order to discourage speculation. Indian rupee exchange rate continued to be pegged to the basket of currencies until early 1990s when market determined exchange rate was introduced.
During 1970s, changes in real exchange rate were largely conditioned by the prices in India and its trading partners as real effective exchange rate (REER) depreciated by an average of about 2 per cent while nominal effective exchange rate (NEER) appreciated by an average of 0.4 per cent indicating not much of movements. The nominal exchange rate, however, became more active during 1980s and a larger part of the movements in REER were driven by change in NEER. During this period, REER depreciated averagely by 2.0 per cent lower than an average depreciation of 3.0 per cent witnessed by NEER (Table 1).
By the late 1980s and the early 1990s, it was recognised that both macroeconomic policy and structural factors had contributed to balance of payments difficulties. Devaluations by India’s competitors had aggravated the situation. Although exports had recorded a higher growth during the second half of the 1980s (from about 4.3 per cent of GDP in 1987-88 to about 5.8 per cent of GDP in 1990-91), trade imbalances persisted at around 3 per cent of GDP. This combined with a precipitous fall in invisible receipts in the form of private remittances, travel and tourism earnings in the year 1990-91 led to further widening of current account deficit. The weaknesses in the external sector were accentuated by the Gulf crisis of 1990-91. As a result, the current account deficit widened to 3.2 per cent of GDP in 1990-91 and the capital flows also dried up necessitating the adoption of exceptional corrective steps.
Table 1: Real Effective Exchange Rate (REER) and Nominal Effective Exchange Rate (NEER) (36 Countries) |
Period |
Index |
Appreciation (+)/ Depreciation (-) |
REER |
NEER |
REER |
NEER |
1970s* |
161.3 |
220.7 |
-2.1 |
0.4 |
1980s |
153.9 |
208.5 |
-2.0 |
-3.0 |
1990s |
100.9 |
101.7 |
-2.5 |
-5.2 |
2000s |
99.9 |
89.2 |
-0.1 |
-0.5 |
2000-01 |
100.1 |
92.1 |
4.3 |
1.2 |
2001-02 |
100.9 |
91.6 |
0.8 |
-0.6 |
2002-03 |
98.2 |
89.1 |
-2.7 |
-2.7 |
2003-04 |
99.6 |
87.1 |
1.4 |
-2.2 |
2004-05 |
100.1 |
87.3 |
0.5 |
0.2 |
2005-06 |
102.4 |
89.9 |
2.3 |
2.9 |
2006-07 |
98.5 |
85.9 |
-3.8 |
-4.4 |
2007-08 |
104.8 |
93.9 |
6.4 |
9.3 |
2008-09 |
94.4 |
86.2 |
-9.9 |
-8.3 |
* Second half of 1970s. |
Against this backdrop, India embarked on stabilisation and structural reforms in the early 1990s of which trade policies, exchange rate policies and industrial policies formed an integrated policy framework to improve the overall productivity, competitiveness and efficiency of the economic system, in general, and the external sector, in particular. As a stabilsation measure, a two step downward exchange rate adjustment by 9 per cent and 11 per cent between July 1 and 3, 1991 was resorted to counter the massive drawdown in the foreign exchange reserves, to instill confidence among investors and to improve domestic competitiveness. A two-step adjustment of exchange rate in July 1991 effectively brought to close the regime of a pegged exchange rate. Following the recommendations of the High Level Committee on Balance of Payments (Chairman: Dr. C. Rangarajan) to move towards the market-determined exchange rate, the Liberalised Exchange Rate Management System (LERMS) was put in place in March 1992 initially involving a dual exchange rate system. Under the LERMS, all foreign exchange receipts on current account transactions (exports, remittances, etc.) were required to be surrendered to the Authorised Dealers (ADs) in full. The LERMS was essentially a transitional mechanism and a downward adjustment in the official exchange rate took place in early December 1992 and ultimate convergence of the dual rates was made effective from March 1, 1993, leading to the introduction of a market-determined exchange rate regime. The dual exchange rate system was replaced by a unified exchange rate system in March 1993, whereby all foreign exchange receipts could be converted at market determined exchange rates. On unification of the exchange rates, the nominal exchange rate of the rupee against both the US dollar as also against a basket of currencies got adjusted lower, which almost nullified the impact of the previous inflation differential.
From March 1993 began a new chapter in the evolution of the real exchange rate of India wherein market determined nominal exchange rate of the rupee started conditioning the real exchange rate besides relative prices. REER depreciated by an average of 2.5 per cent during 1990s significantly lower that the average depreciation of 5.2 per cent in NEER indicating that transmission of NEER depreciation to REER was controlled to a large extent by relative higher rate of change in domestic prices. During 2000s, both REER and NEER witnessed a marginal average depreciation of 0.1 and 0.5 per cent, respectively.
Section IV
Data Description and Research Methodology
Data Description
The variables used in the present study are real exchange rate (REF) of Indian rupee against USA dollar, differential growth rate between India and USA (DG), government final consumption expenditure as percentage of GDP (GC), foreign exchange assets (FX), terms of trade (TOT) and external openness (OP). Data series are quarterly ranging from Q2 of 1997 to Q2 of 2009. The RER has been calculated taking nominal exchange rate of rupee against US dollar, wholesale price index (WPI) of India and producers’ price index (PPI) of USA. We have used bilateral RER of rupee against US dollar keeping in view that India’s about 80 per cent of the international trade is invoiced in US dollar. Since nominal exchange rate has been taken as rupees per US dollar, increase/ decrease in RER mean depreciation/ appreciation. Due to non-availability of data on sectoral productivity, many studies have used the GDP per capita relative to trading partners as a proxy for the Balassa-Samuelson effect (productivity differential). In the present study, we have used difference in growth rate of India and USA to examine the Balassa- Samulson effect on the RER in the absence of quarterly GDP per capita. Higher growth differential, which has been presumed to be largely driven by traded goods sector, will lead to increase in prices of non-traded goods on account of Balassa-Samuelson effect. Foreign exchange assets have been considered to factor in the impact of
capital flows and net foreign assets on the RER. The terms of trade have been derived taking exports as percentage of exports. The
external sector openness has been taken in broader term and computed
aggregate current and capital account inflows and outflows as
percentage of GDP.
Data on India i.e. nominal exchange rate, WPI, government final consumption expenditure (GC), foreign exchange assets (FX), exports and imports, current account inflows & outflows, capital account inflows & outflows, and gross domestic product (GDP) both at current and constant prices are sourced from Handbook of Statistics of Indian Economy, Reserve Bank of India. Producer’s price index and GDP growth of USA are taken from International Financial Statistics (IFS),
International Monetary Fund (IMF).
Research methodology
A number of unit root tests, viz., Augmented Dickey Fuller (ADF), Dickey Fuller-Generalized Least Square (DF-GLS), Phillips- Perron and KPSS have been used in the present study. ADF test investigates the presence of unit root in time series data. Strong negative numbers of unit root reject the null hypothesis of unit root at some level of confidence. ADF framework to check the stationarity of
time series has been given in following equation :
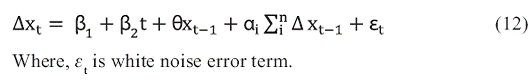 Basically, this test determines whether the estimates of θ are equal to zero or not. Fuller (1976) has provided cumulative distribution of the ADF statistics by showing that if the calculated-ratio (value) of the coefficient is less than critical value from Fuller table, then x is said to be stationary. However, this test is not reliable for small sample data set due to its size and power properties (Dejong et al, 1992; Harris, 2003). For small sample data set, these tests seem to overreject the null hypotheses when it is true and accept it when it is false. Therefore, the findings of ADF test needs to be corroborated with other unit root tests discussed above.
The Phillips-Perron (PP) unit root tests differ from ADF test mainly in how they deal with serial correlation and heteroskedasticity in errors. Particularly, where the ADF tests use a parametric autoregression to approximate the ARMA structure of the errors in the test regression, the PP test ignores any serial correlation. The test regression for the PP test is:
The stationary test is a one-sided right-tailed test so that are rejects the null of stationarity at the 100% level if the KPSS test statistics is greater than the 100.
After testing for integrated order of data series, next logical step is to estimate the relationship with appropriate econometric techniques. Since present study deals with time series data and all the level variables are not stationary, it would be appropriate to apply some technique which can circumvent the problem of stationarity in the time series data. The data could be converted into stationary form taking first difference and relationship could be estimated with ordinary least square (OLS) regression, but there would be greater loss of information and hence, estimates may not be that robust.
Econometric literature has abundant techniques to investigate relationships among non-stationary macroeconomic variables and prominent among them are univariate co-integration technique (Engle-Granger (1987)), multivariate co-integration technique (Johansen (1988); Johansen and Juselius (1990); and Johansen’s (1995)) and newly developed auto regressive distributed lag (ARDL) model (Pesaran and Shin, 1995, 1998; Pesaran et al., 1996; Pesaran et al., 2001). The recent studies indicate that the ARDL approach to cointegration is preferable to other conventional cointegration approaches such as Engle and Granger (1987), Johansen (1988) etc. mainly because of its applicability irrespective of whether the underlying regressors are purely I(0), purely I(1) or mutually cointegrated. The statistic underlying this procedure is the familiar Wald or F-statistic in a generalized Dickey-Fuller type regression, which is used to test the significance of lagged levels of the variables under consideration in a conditional unrestricted equilibrium error correction model (ECM) (Pesaran, et al., 2001). Another reason for preferring the ARDL approach over other approaches is that it is more robust and performs better for small sample sizes.
In the present study, ARDL approach has been used for estimating long-run relationship and short-run dynamics because of the obvious reasons cited above for its preferability i.e. all the variables are not integrated of the same order and small sample is size. The ARDL approach involves estimating the conditional error correction version of the ARDL model for variables under estimation. The conditional VECM in the ARDL framework of interest of the present study could be specified as under :
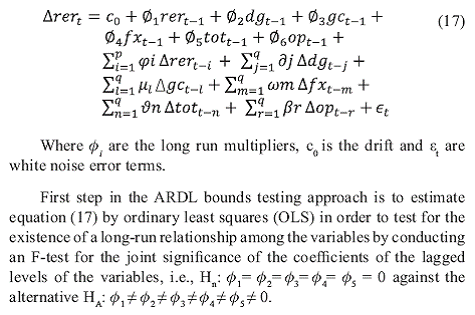 Two asymptotic critical values bounds provide a test for cointegration when the independent variables are I(d) (where 0 ≤d ≤1); a lower value assuming the regressors are I(0) and an upper value assuming purely I(1) regressors. If the F-statistic is above the upper critical value, the null hypothesis of no long-run relationship can be rejected irrespective of the orders of integration for the time series. Conversely, if the test statistic falls below the lower critical value the null hypothesis cannot be rejected. Finally, if the statistic falls between the lower and upper critical values, the result is inconclusive. The approximate critical values for the F test have been obtained from Narayan, P. (2005).
Bounds test has several advantages over the traditional residual based cointegration analysis. First, it is applicable irrespective of the degree of integration of the variables and thus avoids the pre-testing of the order of integration of the variables. In the literature, testing of unit-root properties becomes particularly problematic where the power of unit root test are typically low, and there is switch in the distribution function of the test statistics as one or more roots of the data series approach unity (Pesaran and Pesaran, 1997). Second, unlike residual based cointegration analysis, the unrestricted error correction model (UECM) employed in bound testing does not push the short-run dynamics into the residual terms (Banerjee et al., 1993). Third, the bounds test can be applied to small sample size. Fourth, it identifies the exact variable to be normalised in the long-run relationship. A limitation of bounds test, however, is that it is not appropriate in situations where there may be more than one long-run relationship among the variables. In other words, the test is appropriate only when one variable is explained by the remaining variables and not vice versa.

Section V
Empirical Results
The results reported in Table 2 show that null hypothesis of ADF unit root is accepted in case of all variables except for ToT but rejected in first difference at 1% level of significance. Similarly, null hypothesis of unit root could not be rejected by DF-GLS unit root test in the levels, while it was not accepted in first difference except for GC and ToT. Both the unit root tests indicate that all the variables considered in the present study are difference stationary I(1) barring TOT which is level stationary I(0) only as per ADF test.
Phillips-Perron (PP) unit root test indicates that null hypothesis of unit root cannot be rejected in the level form in case of RER, DG, and OP, but discarded null hypothesis of unit root in GC and TOT in the level form. PP test, however, rejected the null hypothesis of unit root in the first difference of the RER, DG, TOT and OP. The results of KPSS stationary test have rejected the null of stationary in the level of DG, GC, FX, and OP, while accepted the null in the level of RER and TOT. The KPSS results further have found that null of stationary was accepted in the first difference of DG, GC, FX, and OP.
Table 2 : Results of Unit Root/ Stationary Tests |
Variables |
ADF Test |
DF-GLS Test |
Level |
1st Difference |
Level |
1st Difference |
RER |
-1.79 |
-5.17*** |
-1.52 |
-5.15*** |
DG |
-0.61 |
-5.87*** |
0.38 |
-7.65*** |
GC |
-0.74 |
-19.81*** |
-1.09 |
-0.70 |
FX |
2.91 |
-4.06*** |
0.10 |
-3.99*** |
TOT |
-2.83* |
-7.51*** |
0.14 |
0.95 |
OP |
0.66 |
-8.72*** |
-0.37 |
-8.33*** |
Variables |
Phillips-Perron Test |
KPSS Test |
Level |
1st Difference |
Level |
1st Difference |
RER |
-2.05 |
-5.17*** |
0.36* |
0.15*** |
DG |
-1.83 |
-9.92*** |
0.91 |
0.03*** |
GC |
-5.08*** |
-30.92*** |
0.83 |
0.29*** |
FX |
0.40 |
-2.95*** |
0.83 |
0.21*** |
TOT |
-2.85* |
-19.17*** |
0.63** |
0.14*** |
OP |
-0.38 |
-8.71*** |
0.78 |
0.16*** |
Note: ***, **, and * denote statistical signifi cance at 1%, 5% and 10% levels, respectively. |
On the basis of the majority criteria, it has been inferred that variables, viz., RER, DG, GC, FX and OP are integrated of order one I(1), while TOT is integrated of order zero I(0). After seeing the unit root properties of the data series, cointegration among the variables have been tested using auto regressive distributed lag (ARDL) model has been used.
In order to test the presence of long-run relationship between RER and DG, GC, FX, and OP, equation (17) is estimated. A generalto- specific modeling approach guided by the short data span and SBC respectively to select a maximum lag order of 4 for the conditional ARDL-VECM is preferred because of quarterly frequency.
Firstly, an OLS regression is estimated for the first differences part of equation and then tested for joint significance of the parameters of the lagged level variables. The joint null hypothesis of the coefficients being equal to zero means no long-run relationship has been tested with F-statistics. The presence of cointegration between the variables is accepted if F-statistics reject the null at 95 per cent critical bound values generated by Narayan (2005) for small sample. The calculated F statistic presented in Table 3 is 4.8559 and is higher than the upper bound at 1% level of significance. Thus, null hypothesis of no cointegration is rejected, implying that there exists a long-run relationship among the variables RER, DG, GC, FX, TOT, and OP, when the regression is normalized on RER. It may, however, be noted that null hypothesis of no cointegration is accepted at 95 per cent critical value when regression is normalised on variables other than RER. This implies that there exists only one long-run cointegrating relationship.
Having established that a long-run cointegration relationship exists between dependent variable RER and independent variables DG, GC, FX, TOT and OP, the long-run relationship has been estimated using the specification defined in equation (18). The maximum time lag of 4 was selected based on Schwarz’s Bayesian Criterion (SBC).
Table 3 : Bound Test for Cointegration |
Dependent Variable (Intercept and no trend) |
SBC Lag |
F-Statistic |
Probability |
Outcome |
FRER(RER│DG, GC, FX, TOT, OP) |
1 |
4.8559*** |
0.001 |
Cointegration |
FDG(DG│RER, GC, FX, TOT, OP) |
1 |
0.8879 |
0.517 |
No Cointegration |
FGC(GC│RER, DG, FX, TOT, OP) |
1 |
0.8109 |
0.575 |
No Cointegration |
FFX(FX│RER, DG, GC, TOT, OP) |
1 |
3.2669 |
0.108 |
No Cointegration |
FTOT(TOT│RER, DG, GC, FX, OP) |
1 |
1.5692 |
0.194 |
No Cointegration |
FOP(OP│RER, DG, GC, FX, TOT) |
1 |
1.6110 |
0.354 |
No Cointegration |
Critical Values |
T |
1% Level |
5% Level |
10% Level |
I(0) Lower Bound |
I(1) Upper Bound |
I(0) Lower Bound |
I(1) Lower Bound |
I(0) Upper Bound |
I(1) Lower Bound |
Narayan P (2005) |
45 |
3.593 |
4.981 |
2.694 |
3.829 |
2.276 |
3.297 |
50 |
3.543 |
4.839 |
2.670 |
3.781 |
2.259 |
3.264 |
***Significant at 1 per cent level. |
The estimated coefficients of the long-run relationship show that productivity differential (DG) has a statistically significant negative impact on real exchange rate, which is in line with theoretical argument that increase in productivity differential leads to higher price level and eventually result into appreciation of RER. Similarly, the long-run coefficients of FX and TOT have negative sign and are significant at 1% level, indicating that increase in forex exchange assets and terms of trade affect appreciation in RER, which is again in tandem with a priori. The long-run coefficient of OP is positive and significant at 1% level of significance implying that augmenting external sector openness result into depreciation of RER and is consistent with theoretical argument as well as results of numerous studies undertaken in the past with reference to different countries. The coefficient of GC is positively signed and against the theoretical argument, but it is not statistically significant even with wider confidence intervals (Table 4). The results of long-run relationship establish that DG, FX, TOT and OP are main determinants of real exchange rare in India.
Table 4 : Estimated Long-run Coefficients using ARDL Model |
ARDL(1,0,0,0,0,0) selected based on SC. Dependent variable RERt. |
Regressor |
Coeffi cient |
Standard Error |
T-Ratio |
Probability |
DGt |
-0.28419** |
0.14405 |
-1.9729 |
0.056 |
GCt |
0.068204 |
0.11720 |
0.58196 |
0.564 |
FXt |
-0.0001162* |
0.00001579 |
-7.3587 |
0.005 |
TOTt |
-0.11589* |
0.024582 |
-2.9880 |
0.000 |
OPt |
0.13259* |
0.033447 |
3.9642 |
0.000 |
C |
55.7714* |
3.6230 |
15.3935 |
0.000 |
Note: *, **, and *** denote statistical significance at 1%, 5% and 10% level, respectively. |
It has also been explored whether actual RER is far away from the RER fitted by the selected fundamentals. It could be seen from Chart 1 that actual RER largely follows the fitted RER implying that there has not been any major deviations in the actual RER from its long-run path fitted by fundamentals in India.
Furthermore, short-run dynamics from error correction have been estimated within the ARDL framework given in equation (19). It could be seen in Table 5 that signs of short-run dynamic impact are consistent with long-run coefficients. Error correction term is negative and significant at 1% significant level implying that there is convergence to long-run equilibrium path. The coefficient of the ECM is very high at (-) 0.46 implying a fairly high speed of adjustment to the long-run disequilibrium after a shock. Approximately 46 per cent of the deviation in RER from the long-run equilibrium level is corrected in the next quarter.
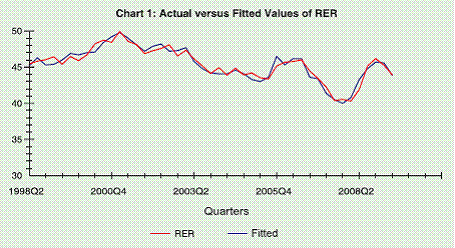
Table 5: Error Correction Representation for the Selected ARDL Model |
ARDL(1,0,0,0,0,0) selected based on SC. Dependent variable ΔRERt. |
Regressor |
Coeffi cient |
Standard Error |
T-Ratio |
Probability |
dDGt |
-0.13037** |
0.59660 |
-2.1835 |
0.035 |
dGCt |
0.031263 |
0.052436 |
0.59621 |
0.555 |
dFXt |
-0.0001162* |
0.00001579 |
-7.3587 |
0.000 |
dTOTt |
-0.053123* |
0.012488 |
-4.2540 |
0.000 |
dOPt |
0.060777* |
0.013592 |
4.4714 |
0.000 |
dC |
25.5644* |
4.7553 |
5.3760 |
0.000 |
Ecm(-1) |
-0.45838* |
0.077881 |
-5.8856 |
0.000 |
Note: *, **, and *** denote statistical significance at 1%, 5%, and 10% level, respectively. |
Section VI
Concluding Remarks
The volatility and misalignment of RER from its equilibrium level adversely affects the competitiveness and economic growth of developing countries as non-tradable goods constitute a large segment of the goods market. Therefore, RER stability and alignment have assumed critical importance in policy formulations particularly in EMEs and developing countries to improve economic performance during recent years. Given the fact that RER movements and economic growth have got some association positive or negative, the determinants of RER have become important. The macroeconomic fundamentals viz., productivity differential, capital flows/foreign exchange assets, government consumption, terms of trade, external sector openness have been given as main determinants of RER. Balassa and Samuelson hypothesis provides that productivity differential in traded and nontraded sectors cause rise in the price level of an open economy and appreciation of the home country’s real exchange rate. A surge in capital flows leads to an increase in aggregate demand and rise in the price of non-traded goods, which would eventually reflect in appreciation of the real exchange rate. Furthermore, excess capital flows would lead to nominal appreciation in exchange rate. The government expenditure, which is disproportionately incurred on non-traded goods, leads to upward pressure on relative price of non-traded goods and appreciation in exchange rate. The deterioration in terms of trade generates negative income effect leading to decline in prices and eventually resulting into real depreciation of the exchange rate, while, at the same time it induces substitution effect in favour of non-traded goods increasing their prices and real appreciation in exchange rate. Increasing external openness of an economy may increase demand for imported goods and decline for demand of non-traded goods, which would result to decline in the prices of non-trade goods and real exchange rate depreciation. The impact of aforementioned macroeconomic fundamentals has been tested estimating ARDL cointegration model.
The bound tests of cointegration indicate that there exist a long-run relationship between RER and independent variables viz., differential growth, government consumption, net foreign assets, terms of trade and openness. The estimated coefficients of the long-run relationship show that productivity differential (differential growth), net foreign assets and terms of trade have negative sign and are significant at 1% significance level, indicating that increase in these variables lead to appreciation in RER. The long-run coefficient of openness is positive and significant at 1% level of significance implying that augmenting external sector openness result into depreciation of RER. The coefficient of government consumptions is, however, positively signed but it is not satistically significant. Therefore, the results of long-run relationship establish that productivity differential, foreign assets, terms of trade and openness are main determinants of real exchange rare in India. Productivity differential exerts largest influence on the RER. Further, the signs of the short-run dynamic impact have been found consistent with long-run coefficients and error correction term is negative and significant implying convergence to long-run equilibrium path. About 46 per cent at the deviation in the long-run equilibrium RER is corrected during the next quarter.
The appreciation in RER is generally seen as deterioration in the competitiveness of the traded goods sector. The results of present study, however, shows that appreciation in RER should not always be seen as decline in competitiveness as some of the factors contributing to appreciation in RER viz., increase in productivity differential and net foreign exchange assets and decline in terms of trade are attributed to higher growth reflecting improvement in the traded goods sector competitiveness.
Notes:
* Assistant Adviser with Department of Economic Analysis and Policy, Reserve Bank of India. The views expressed in the paper are those of author and do not necessarily represent those of the RBI. Errors and omissions, if any, are the sole responsibility of the author. The author is extremely thankful to Dr. M.R. Aggarwal for providing valuable guidance in accomplishing this study.
1 While theoretically, capital flows would equal to zero in the long-run, most less developed countries are expected to be capital importers for the future, therefore, most empirical studies of developing economies use a measure of sustainable capital flows rather than a zero capital account. Models of the RER in these countries often include capital flow as a determinant of the equilibrium
real exchange rates (see Joyace and Kamas (2003)).
References :
Aguirre and Calderon, (2005), “Real Exchange Rate Misalignments and Economic Performance,” Working Paper No. 316, Central Bank of Chile. Antonia, L.V. & Josep, L.R. Bara (2006), “The short and long-run determinants of the real exchange rate in Mexico,” Working Paper No. 0606, Department of Applied Economics at Universidad Autonoma of Barcelona.
Antonia, L.V. (2006), “Real equilibrium exchange rates. A panel data approach for advanced and emerging economies,” Working Paper No. 0605, Department of Applied Economics at Universidad Autonoma of Barcelona.
Balassa, B. (1964), “The purchasing power parity doctrine: a reappraisal”,
The Journal of Political Economy, Vol.72, 584–96.
Balassa, B. (1973), “Just how misleading are official exchange rate
conversions: a comment”, Economic Journal, 83, 1258–67.
Clark, P. B, and MacDonald, R. (1998), “Exchange rates and economic fundamentals: a methodological comparison of BEERs and FEERs”, IMF
Working Paper No. 67, International Monetary Fund, Washington D C.
Clark, P. B, and MacDonald, R. (2000), “Filtering the BEER: a permanent and transitory decomposition”, IMF Working paper No. 144, International
Monetary Fund, Washington D C.
Clark, P. B, Bartolini, L., Bayoumi, T. & Symansky, S., (1994), “Exchange rates and economic fundamentals: a framework for analysis,” IMF
Occasional Paper No. 115, International Monetary Fund, Washington D. C.
Cottani, J.A., Cavallo, F. and Khan, Shahbaz (1990), ”Real Exchange Rate Behavior and Economic Performance in LDCs”, Economic Development
and Cultural Change, Vol.39:61-76.
De Gregorio J., Giovanni, A. and Wolf, H. C. (1994), “International evidence on tradables and non-tradables inflation”, European Economic Journal, Vol. 38, 1225–44.
Diaz-Alejandro, Carlos F (1963), “A Note on the Impact of Devaluation and the Redistributive Effect,” The Journal of Political Economy, Vol.71
December.
Drine, Imed and Rault, Christophe (2005), “Can the Balassa-Samuelson theory explain long-run real exchange rate movements in OECD countries?”, Applied Financial Economics, Vol.15: 8, 519-530.
Edwards, Sebastian, (1989), “Real Exchange Rate, Devaluation and Adjustment”, The MIT Press, Cambridge.
Elbadawi, I., A. (1994), “Estimating Long-Run Equilibrium Exchange Rates” in Williamson, John, (eds), Estimating Equilibrium Exchange Rates, Institute for International Economics, Washington DC.
Elbadawi, Ibrahim, A. and Soto Raimundo, (1997), “Real Exchange Rates and Macroeconomic Adjustment in Sub-Saharan Africa and Other Developing Countries,” Journal of African Economies, Vol. 6(3), pages 74- 120, Oxford University Press.
Froot, Kenneth A., and Kenneth Rogoff (1996), “Perspectives on PPP and Long-Run Real Exchange Rates,” NBER Working Paper No. 4952, April.
Ghura, D. and Grennes, T., J. (1993), “The Real Exchange Rate and Macroeconomic Performance in Sub-Saharan Africa”, Journal of Development Economics, Vol. 42: 155-174.
Hau, Harald (2006), “The Role of Transaction Costs for Financial Volatility: Evidence from the Paris Bourse,” Journal of the European Economic Association, MIT Press, vol. 4(4), pages 862-890, 06.
Hsieh, D., (1982), “The determination of the real exchange rate: the productivity approach”, Journal of International Economics, Vol. 12:355- 24362.
Jorge Carrera and Romain Restout, (2008), “Long Run Determinants of Real Exchange Rates in Latin America,” Post-Print halshs-00276402_v1, HAL. Krugman, Paul and Taylor, Lance (1978), “Contractionary effects of devaluation,” Journal of International Economics, Elsevier, Vol. 8(3), pages 445-456.
Krumm, K. (1993), “A Medium-Term Framework for Analysing the Real Exchange Rate, with Applications to the Philippines and Tanzania”, World
Bank Economic Review, Vol. 7 : 219-49.
Lane, P., and G. Milessi-Ferreti (1999), “The External Wealth of Nations: Measures of Foreign assets and Liabilities for Industrial and Developing Countries,” CEPR Working Paper No. 2231.
Lizondo, Saul and Peter J. Montiel (1989), “Contractionary Devaluation in Developing Countries: An Analytical Overview”, IMF Staff Papers, Vol. 36, pp. 182-227.
Maeso-Fernandez, F., C. Osbat, and B. Schnatz (2001), “Determinants of the Euro Real Effective Exchange Rate: a BEER/PEER Approach,” European Central Bank Working Paper No. 85.
Montiel, P.(1999a), “Determinants of the long run equilibrium real exchange rate: An analytical model”, in L. Hinkle and P. Montiel (eds.), Exchange rate misalignment: concepts and measurements for developing countries, World Bank, Washington D.C, pp. 264-290.
Montiel, P. (1999b), “The long run equilibrium real exchange rate: Conceptual issues and empirical research”, in L. Hinkle & P. Montiel (eds.), Exchange rate misalignment: concepts and measurements for developing countries, World Bank, Washington D.C, pp. 219-263.
Obstfeld, K. and Rogoff, P. (1996), “Foundation of International Macroeconomics”, MIT Press, Cambridge, MA.
Pesaran, H.M and Pesaran, B (1997), “Working with Microfit 4.0, Oxford University Press”, Oxford.
Pesaran, H.M., Shin, Y. and Smith, R.J. (2000), “Structural analysis of vector error correction models with exogenous I(1) variables”, Journal of Econometrics, 97, pp. 293-343.
Razin, O., and Collins, S. M.(1997), “Real exchange rate misalignment and growth”, Retrieved: March 2005”, available at http://econwpa.wustl.edu:80/eps/if/papers/9707/9707001.pdf
Rogoff, K. (1996), “The purchasing power parity puzzle”, Journal of Economic Literature, Vol.34, pp.647-668.
Rosenberg, M. R.(2003), “The dollar’s equilibrium exchange rate: a market view”, in Dollar Overvaluation and the World Economy, Institute for International Economics, Washington, pp.35-55.
Samuelson, P. (1964), “Theoretical notes and trade problems,” Review of Economics and Statistics, Vol. 46, pp.145-54.
Sekkat, Khalid & Varoudakis, Aristomene (2000), “Exchange rate management and manufactured exports in Sub-Saharan Africa,” Journal of
Development Economics, Elsevier, Vol. 61(1), pages 237-253, February. |