Saurabh Ghosh and Snehal Herwadkar*

We analyse the effect of portfolio flows on various segments of the Indian financial markets over the decade preceding the global financial crisis. The correlation analysis and the causality test results suggest that portfolio flows cause changes in equity prices and exchange rates. In the short run, the VAR and impulses response functions indicate that a positive shock to net FII flow generally result in increase in equity prices, exchange rate (INRUSD) appreciation and a decline in interest rates. The magnitude of these responses dampens over time and converges towards equilibrium path. In the long run, the parameters of Autoregressive Distributed Lag (ARDL) Model indicate the existence of an equilibrating relation. The magnitude and direction of long term coefficients generally support the short run findings. The negative and significant error correction term, on the other hand, indicates movements towards long run equilibrium and the resilience of Indian financial markets.

JEL Classification : G11, G14

Keywords : Portfolio flow, Financial Markets

I. Introduction

The decade immediately preceding the global financial crisis (1998-2008) had witnessed an exponential increase in international capital movements, especially in the emerging markets. India was no exception to this phenomenon, where with the ushering of economic liberalisation and globalisation there was a large increase in the portfolio inflows. The favourable demographic characteristics (Mohan, 2004), growth potential, scope of diversification and economic policies also influenced India’s share in capital flows among Emerging Market Economies (EMEs). Consequently, the Indian financial markets started getting increasingly integrated with the global financial market (Sinha and Pradhan, 2008). Anecdotal evidence suggest that global factors started influencing domestic markets through the portfolio channel over the last decade.

It is well established in the literature that financial markets suffer from contagion – both foreign and domestic [Lagoarde and Lucey (2007)]. While the former refers to a shock to a country’s financial markets caused by changes in markets of another country, the latter refers to turbulence in one market spilling over to other market segments of the same country. These movements across financial markets are often synchronous in nature, particularly in EMEs. These two effects often reinforce each other and amplify the problem.

The East Asian crisis clearly indicated the vulnerability of an open economy to sudden changes in portfolio flows. With gradual progress towards external sector liberalisation and increasing capital inflows, the issues relating to the resilience of Indian financial system in the face of strong and volatile capital flows attained increasing importance. The present study is an attempt to address these issues. It aims to analyse the effects of portfolio flows across different financial markets. Specifically, this study has two objectives: it attempts to model the short run and long run relationship between the portfolio flows and different segments of the financial market. Second, it intends to assess the impact of sudden changes in such flows on various segments of the financial markets. This paper is organised as follows: Section II presents a brief survey of literature, Section III describes the data, Section IV analyses the empirical findings and Section V draws conclusions.

Section II
Literature Survey

One of the major arguments in favour of the financial liberalisation and globalisation is that it facilitates greater economic growth. Many economists also believe that free capital flows will lead to a more efficient allocation of resources (e.g. Kim and Singal, 2000). Considering the beneficial role played by capital flows, early research interest was focused on the determinants of such flows. For instance, studies by Taylor and Sarno (1997), Brennan and Cao (1997), Mody and Murshid (2005) and Lagoarde and Lucey (2007) concentrated on the determinants of the portfolio investment and their impact on the receiving economies. Their empirical findings, though not unanimous, generally point towards productivity growth and allocative efficiency of the capital flows.

Towards the end-1990s, especially after the outbreak of economic crisis in South East Asian countries, issues such as volatility of the ‘hot’ capital flows and their impact on the recipient country, problems relating to contagion etc. have increasingly occupied the centre-stage of academic research. Subsequently, many policy makers and economists became skeptical not only about the benefits of free flows, but also viewed uncontrolled capital flows as risky and destabilising. Krugman (1998) underlined the problem of moral hazard in financial intermediaries and noted that it can lead to over-investment at the aggregate level, overpricing of assets and vulnerability of such economies to financial crises. Subsequent studies (e.g. Dabos and Juan-Ramon (2000)) concentrated on the intricate relationship between capital flows and financial markets. The recent literature has acknowledged the risks associated with the capital flows and indicated that the most effective way to deal with capital inflows would be to deepen the financial markets, strengthen financial system supervision and regulation, improve capacity and implement sound macroeconomic / financial sector policies. These actions will help in increasing the absorptive capacity and resilience of the economies and financial systems to the risks associated with large and volatile inflows. To quote Mohan (2009), ‘It is a combination of sound macroeconomic polices, prudent debt management, exchange rate flexibility, the effective management of the capital account, the accumulation of appropriate levels of reserves as self-insurance and the development of resilient domestic financial markets that provides the optimal response to the large and volatile capital flows to the EMEs. How these elements are best combined will depend on the country and on the period: there is no ‘one size fits all’’.

Since the beginning of 2000s, empirical studies have concentrated on capital flows in India and its impact on domestic macro variables. In this context a study by Dua and Sen (2005) found that the real effective exchange rate is cointegrated with the level of capital flows, volatility of the flows, high-powered money, current account surplus and government expenditure. The results reported by Trivedi and Nair (2000) indicate that the returns and volatility in the Indian markets emerge as the principal determinants of FII investments. D’souza (2008) noted that the difference between the capital flows to India as compared with other EMEs are that (a) they are associated with a deteriorating current account position rather than improving one and (b) the extent of financial outflows have only partially offset the capital inflows. The author also notes that capital flows in India have been associated with a buoyant stock market and a rise in investment and interest rates in the economy.

While most of the previous empirical studies considered impact of capital flows on the macroeconomic variables or on a particular market (e.g. stock market / exchange rate market etc.) our study attempts to integrate the major financial markets and evaluate the market reaction to a shock in capital flows. In other words, the emphasis is on market dynamics and resilience to uncertain and volatile flows rather than analysing the determinants or the effect of capital flows on domestic variables. It assumes significance as India moves towards greater capital account liberalisation (A brief write-up on India’s approach to capital flows is reported in the Annex I), and faces the challenges of coping with large, volatile and uncertain capital flows.

Section III
Data

The major data-source for this study is Handbook of Statistics on the Indian Economy (HBS). Our study uses the monthly time series data on financial variables over the decade just before the outbreak of global financial crisis(April 1998 to March 2008). The period 2008-09, which was mainly characterised by exterme events and freezing of financial markets, was not included in the empirical analysis as it may distort the general trends observed in the financial markets. However, results obtained were compared with reference to this period, which serves as a robustness test.

We used rupee dollar (INRUSD) exchange rate to represent the movements in forex market and yields of benchmark 10-year Government of India securities (GSEC) as a representation of gilt movements. While for the equity market, monthly average data for BSE Sensex (Sensex) has been used, the monthly average call / notice rate (CALL) is used for representing the interbank money market. The monthly data on net investments in debt and equity by foreign institutional investors (NETFII) were gathered from the Securities and Exchange Board of India web-site. Table-1 reports the descriptive statistics for these variables.

It may be noted that the FII flows in Indian markets consist of investments in equities as well as in debt instruments. Even though the FII investments in equities have consistently remained much higher than the same in debt instruments, the FII investments in debt have almost doubled during 2007-08 as compared with 2006-07. Unlike some of the earlier studies, in view of the growing investment of FIIs in debt instruments, we have used both of these flows in the present paper.

Section IV
Methodology and Empirical Findings

IV.1 Basic Results

The objective of this paper is to study the interrelationship of portfolio flows in India with other financial variables. Following the standard time series methodology, we first check for stationarity of these variables. This involves determining the order of integration of each of the variables under consideration by employing one of the unit root tests. In this paper we employ the widely accepted Phillips- Perron (1988) t-test. The results are reported in Table 2 below.

The Phillips-Perron adjusted t-stat and their p-values indicate that CALL and NETFII are both stationary at levels. The SENSEX, GSEC and INRUSD rate are first difference stationary. The correlation coefficients of the above variables are reported in Table 3. For computing the correlation coefficients the non-stationary series are included in the differenced form (to avoid spurious results), while the stationary variables are in the levels.

Table 3 indicates that NETFII has a high positive coefficient with changes in SENSEX and negative correlation coefficient with other financial rate variables (CALL, GSEC and INRUSD). So, an increase in NETFII could lead to an increase in SENSEX, reduction in interest rates and put an appreciating pressure on INR.

IV.2 Causality Analysis

In the previous section we found some evidence of contemporaneous relation between the financial variables with net capital inflow in India. This section examines the possibility of leadlag relationship among these financial variables. For evaluating the same we considered Granger causality test¹. Table 4 reports the null hypothesis, Granger F-Statistics and the probability values associated with the F-statistics.

Table 4 indicates that NETFII causes changes in SENSEX and INRUSD. There are also empirical evidences of CALL causing changes in SENSEX and Yield. The F-Statistics and the associated P-values indicate bi-directional causality between CALL and INRUSD.

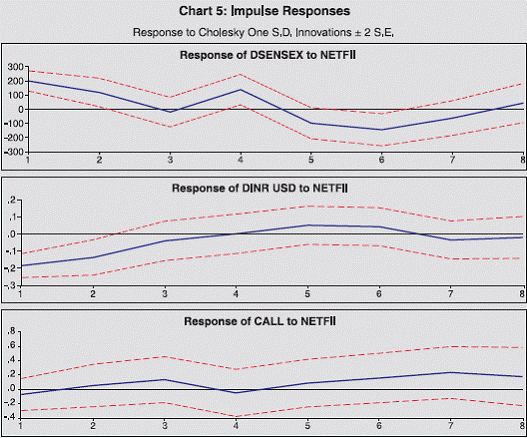
IV.3 Short Run Adjustments: Impulse Responses

In order to examine the directional impact and the time path of a change in NETFII flows on other financial variables, we used a basic five variable VAR model comprising of net FII flows (NETFII), exchange rate (INRUSD), Stock indices (SENSEX), Call rate (CALL) and benchmark yield (GSEC). The impulse responses trace out the responsiveness of these variables to a shock to NETFII. The level stationary variables were used in levels for the VAR, whereas the difference stationary variables were used in difference form. The order of the VAR was selected using the SBC criteria. A unit shock was applied to the errors of NETFII equation, and the effects upon the VAR system over time were noted. For generating the impulse responses, we used orthogonalised (Choleski) impulse responses to a unit standard deviation shock; Chart 5 reports these impulse responses along with analytical standard error bands (represented by the dotted lines).

A look at the impulse responses, over an eight-month period, reveals two stylised facts. First, a shock in NETFII has a negative impact on most financial variables. For instance, differenced exchange rate initially declined, indicating appreciation of INR, due to the increase in NETFII flows. The call rate also declined initially, indicating surplus liquidity in the money market. The NETFII flows, on the other hand, had a positive impact on the stock market, indicating the important link between capital flows and the stock prices in India. These results are consistent with the available literature / anecdotal evidence on capital flows and markets in EMEs. The impact of such impulses either dampened over time or hovered around the initial values indicating the resilience of the financial markets in India in the short run.

A simple VAR system and impulse responses are often criticized because ordering of the equations in the VAR system plays a role in the magnitude and direction of impulse responses. To ascertain the robustness of the results, we cross-checked the impulse responses through the Generalised impulses, as introduced by Pesaran and Shin (1998), which in contrast to Choleski decomposition does not depend on the VAR ordering. The impulse responses that are reported in Annex Chart A2 confirm the above findings.

IV.4 Long Term Relation (Cointegration)

In this section we test for the existence of a long-run relationship between NETFII and financial variables within a multivariate framework. The general process for testing the same for a set of nonstationary variables (of same order or integration) is by testing the existence of cointegrating vector(s) using Johansen (1988) method. However, the PP test (Table - 4) indicates that all variables under consideration here do not have the same statistical properties (rather a combination of I(0) and I(1) variables). Therefore, in order to test for the existence of any long-run relation among the variables, we used Autoregressive Distributive Lag (ARDL) method and the bounds testing approach to cointegration. The main advantage of ARDL testing lies in the fact that it can be applied irrespective of whether the variables are I(0) or I(1) [Pesaran et al.(1996)]. The test gives asymptotically efficient long run estimates irrespective of whether the underlying regressors are I(0) or I(1) process. The specification of the ARDL model is as follows :

Given the number of variables (k=4) the relevant critical value bounds for the present application at the 90 per cent level are given by 2.2425 to 3.574. Since F(CALL) = 3.59 exceeds the upper bound of the critical value band, we can reject the Null of no long-run relationship among the variables under consideration.

The estimation of the long-run coefficients and the associated error-correction model can now be accomplished using the ARDL methodology. The order of the ARDL model was selected using both the Schwarz Bayesian (SBC) and the Akaike Information (AIC) criteria and the selected model (using SBC as well as AIC criteria) was of ARDL(1,0,0,0,0) specifications. While the ARDL coefficients are reported in the Annex Table A3 the estimates of the long-run coefficients based on this model are summarised in Table 6 (column 2 and 3) below.

Column 4 and 5 of the Table 6 report the long term coefficients derived from the augmented ARDL model. The augmented model incorporates five additional dummy variables. The LAF Cap dummy captures months (2007M3 – 2007M7) when the reverse repo (absorption) window of Liquidity Adjustment facility³ was capped at Rs.3,000 crore and the money market rate plunged considerably due to excess liquidity in the interbank market. The four end-quarterdummies were incorporated to capture the seasonal patterns in the Indian money market. The rate and volatility in the money market generally increase during the end-quarter mainly due to advance quarterly tax outflow from the system. The quarterly dummies were incorporated in the augmented model to capture the seasonal pattern in the money market. The dummy coefficient for March was significantly different from zero at five percent level. It may be noted from the above table that the point estimates in both the cases are similar in magnitude and signs. They indicate that increasing GSEC yield (rising cost of capital) and Sensex (booming capital market) put upward pressure on money market rates. The capital flows, on the other hand, have an easing impact on the money market rates. This could be due to the fact that during the period of large capital inflows, the central bank’s forex operations⁴ (purchase of dollar), at times, increase liquidity in the domestic money market and therefore have an easing impact on rates. The sign of INRUSD was found to be positive. This could be because of the fact that the periods characterised by INR depreciation are generally marked by large capital outflows, forex operations (sell of dollars) and therefore relatively tight liquidity conditions (higher money market rates). All these coefficients were statistically significant at 10 per cent levels.

The error correction coefficient, (Table 7) estimated using the same ARDL model was at 0.661(0.00), statistically highly significant and had the correct (negative) sign, which suggested reasonable speed of convergence to equilibrium⁵. The ECM coefficient for the augmented model was also consistent with the former and indicated the robustness of these models.

The above error correction model can also be used in forecasting the changes in money market rates due to changes in capital flows and changes in other financial market variables. To test the robustness of the model, forecast for 2008M4 to 2008M7 was done using both the models (simple as well as Augmented ARDL models) which are referred in Table 8 below:

The root mean squares of forecast errors of the estimated period compared favourably with that in the sample period. The RMSE of the Augmented ARDL model was lower, but in line with the former, which supports finding of the earlier models. The actual and estimated values of call rates are plotted in the Annex Chart A-3.

Section V
Conclusion

The literature so far is not unanimous about the movements in the financial markets as a result of capital flows. The present paper evaluates this ongoing debate in the Indian context. The results indicate that net FII flows cause changes in equity (SENSEX) and exchange rate (INRUSD). In the short run, a shock to net FII flow has a positive impact on equity market and negative impact on money market (CALL) rate, benchmark yield and exchange rate (indicating Rupee appreciation). The impulse responses dampen over time.

The capital inflows and returns on equities generally have a positive correlation for emerging markets. The empirical findings of this study confirms the same for India over the last decade. One of the major reasons for surplus liquidity in Indian money market during 2004:04 to 2008:03 was large capital inflows and consequent upward pressure on the Indian Rupee. The Central Bank’s forex operations in the face of large capital inflows had a positive impact on the domestic money supply and interbank liquidity. This in turn put a downward pressure on the rates in the money market. In an attempt to reduce surplus liquidity from the money market, the central bank sterilised excess liquidity (through Open Market Operations or Market Stabilisation Scheme), which influenced the rates in the G-sec market. These calibrated policies have been captured in the short run analysis of the present paper.

Over the long run, the result of the ARDL model generally supports the short run dynamics. The bound test (of ARDL model) indicates that there exists a long run relation between capital flows and financial variables. The error correction term has a negative coefficient and was found to be statistically highly significant, indicating reasonable speed of convergence to the equilibrium. The long run coefficients of the ARDL model for yield, exchange rate (increase indicate rupee depreciation) and equity had a positive effect on call rate, while the net FII inflow has a negative effect on the same. The long term coefficients of the ARDL model and the negative and significant error correction term, indicates the resiliance of Indian financial markets.

Finally, this study mainly concentrated on the pre-global crisis period to evaluate the long term interaction between financial variables during normal times. Though the impact of the recent global crisis was rather muted for the Indian economy, some capital outflows were witnessed during September-October 2008, with concomitant pressure on the financial markets. However, because of the pre-emptive policy measures and the resilience of the financial system, the markets were back to normal by December 2008. While the quick adjustment and resilience demonstrated by the markets reinforce the empirical findings of our study, it also opens up several areas for further research (e.g. contingency measures and the reaction of various financial markets in response to such measures). With the availability of longer time series data, these issues can trigger off more focussed research on financial markets and capital flows, which would serve as a useful guide both in refining operating procedures and furthering financial markets reforms in India.

Annex I : The Indian Approach to Capital Flows : An Overview

Until the 1980s, India’s development strategy was focussed on selfreliance and import-substitution. There was a general disinclination towards foreign investment or private commercial flows. Since the initiation of the reform process in the early 1990s, however, India’s policy stance has changed substantially. India has encouraged all major forms of capital flows, though with caution, in view of concerns for macroeconomic stability. The broad approach to reform in the external sector after the Gulf crisis was delineated in the Report of the High Level Committee on Balance of Payments (Chairman: C. Rangarajan). The Report, inter alia, recommended a compositional shift in capital flows away from debt to non-debt creating flows; strict regulation of external commercial borrowings, especially short-term debt; discouraging volatile elements of flows from non-resident Indians; gradual liberalisation of outflows; and disintermediation of Government in the flow of external assistance. In the 1990s, foreign investment has accounted for a major part of capital inflows to the country. The broad approach towards foreign direct investment has been through a dual route, i.e., automatic and discretionary, with the ambit of the automatic route progressively enlarged to many sectors, coupled with higher sectoral caps stipulated for such investments. Portfolio investments are restricted to select players, viz., Foreign Institutional Investors (FIIs). In respect of NRI deposits, some control over inflows is exercised through specification of interest rate ceilings. In the past, variable reserve requirements were stipulated to modulate such flows. At present, however, reserve requirements are uniform across all types of deposit liabilities (see, for instance, RBI, 2004b).

In connection with external assistance, both bilateral and multilateral flows are administered by the Government of India and the significance of official flows has declined over the years. Thus, in managing the external account, adequate care is taken to ensure a sustainable level of current account deficit, limited reliance on external debt, especially short-term external debt. Non-debt creating capital inflows in the form of FDI and portfolio investment through FIIs, on the other hand, are encouraged. A key aspect of the external sector management has, therefore, been careful control over external debt since 1990s (Reddy, 1998). India has adopted a cautious policy stance with regard to short-term flows, especially in respect of the debt-creating flows.

In respect of capital outflows, the approach has been to facilitate direct overseas investment through joint ventures and wholly owned subsidiaries. Exporters and exchange earners have also been given permission to maintain foreign currency accounts and use them for permitted purposes to facilitate their overseas business promotion and growth. Thus, over time, both inflows and outflows under capital account have been gradually liberalised.

Annex II

Notes :

* Saurabh Ghosh is an Assistant Adviser working in the Financial Markets Department and Snehal Herwadkar is an Assistant Adviser working with the Department of Economic Analysis and Policy, Reserve Bank of India. The views expressed here are that of the authors alone and do not necessarily represent the official policy stance of the Reserve Bank of India.

¹ If the variable y₁ causes y₂, lag of y₁ would be jointly significant in the equation of y₂. The joint significance of the lags were evaluated with the help of Granger F-test and the lag lengths have been selected using the minimum value of Schwarz – Bayesian Information Criteria (SBC).

² Two sets of critical value are given. One set assuming that all variables in the ARDL model are I(1), and other computed assuming all the variables are I(0).

³ A tool used in monetary policy that allows banks to borrow money through repurchase agreements. Repo (Reverse Repo) indicates injection (absorption) of liquidity by central bank in (from) the banking system.

⁴ The exchange rate policy in recent years in India has been guided by the broad principles of careful monitoring and management of exchange rates with flexibility, without a fixed target or a pre-announced target or a band, coupled with the ability to intervene, if and when necessary. The overall approach to the management of India’s foreign exchange reserves takes into account the changing composition of the balance of payments and endeavours to reflect the ‘liquidity risks’ associated with different types of flows and other requirements (First Quarter Review of Annual Monetary Policy for the Year 2008-09).

⁵ The larger the error correction coefficient the faster is the economy’s return to its equilibrium, once shocked.

References

Agarwal R. (1997), ‘Foreign Portfolio Investment In Some Developing Countries: A Study of Determinants and Macroeconomic Impact’, Indian Economic Review, vol. 32, issue 2, pages 217-229.

Alfaro, L., Chanda, A., Kalemli-Ozcan, S., Sayek, S. (2003), ‘FDI Spillovers, Financial Markets and Economic Development’, IMF Working Paper No. 03/186

Brennan, M., Cao, H. (1997), ‘International Portfolio Investment Flows’, Journal of Finance, December, 52(5): 1851-80.

Chakrabarti, R. (2001), ‘FII Flows to India: Nature and Causes’, Money and Finance, Vol. 2, No. 7, October-December 2001

Dabos, M. and V. Juan-Ramon, 2000. Real Exchange Rate Response to Capital Flows in Mexico: An Empirical Analysis, IMF Working Paper, WP/00/108, June.

D’Souza, E. (2008), ‘Globalisation’s Underbelly: Capital Flows and Indian Economy’, Economic and Political Weekly, August 30, 2008.

Detragiache, E., P. Gupta, (2004), ‘Foreign Banks in Emerging Market Crises: Evidence from Malaysia’, IMF Working Paper, wp04129.

Dua, P., and Sen P., 2005. Delhi School of Economics, University of Delhi, mimeo.

Froot, K., Thornton, D. (2002), ‘The Persistence of Emerging Market Equity’, ‘Emerging Markets Review’. December; 3(4): 338-64

Gordon, J., Gupta, P. (2003), ‘Portfolio Flows into India: Do Domestic Fundamentals Matter?’ Working Paper No. 03/20, January.

Gupta, P. (2005), ‘Macroeconomic Determinants of Remittances: Evidence from India’, IMF Working Paper, wp05224.

Johansen, S. (1988), ‘Statistical Analysis of Cointegrated Vector’, Journal of Economic Dynamics and Control, 12, 231-54

Kim, E., Singal, V. (2000), ‘The Fear of Globalizing Capital Markets’, Emerging Markets Review, November, 1(3): 183-98

Kohli, R, (2003), ‘Capital Flow and Domestic Financial Sector in India’, Economic and Political Weekly, February.

Krugman, P. 1998. ‘What Happened to Asia?’ Manuscript. MIT. January.

Levine, R. (2001), ‘International Financial Liberalization and Economic Growth’, Review of International Economics, November; 9(4): 688-702.

Lagoarde-Segot, T. and Lucey, B. (2006), ‘Financial Contagion in Emerging Markets: Evidence from the Middle East and North Africa’, The Institute for International Integration Studies Discussion Paper Series, iiisdp114, IIIS.

Mody, A., Murshid, A. (2005), ‘Growing Up with Capital Flows’, Journal of International Economics, January, 65(1): 249-66.

Mohan, R. (2004), Fiscal Challenges of Population Aging: The Asian Experience, speech at the symposium sponsored by the Federal Reserve Bank of Kansas City, August 26 – 28.

Mohan, R. (2005), ‘Indian Economy in a Global Setting’, Address Delivered at the Indian Merchants Chamber, Mumbai, September

Mohan, R. (2009), Capital Flows and Emerging Market Economies, CGFS Papers No. 33, Bank for International Settlements, January.

Otker-Robe, I. Polanski, Z., Topf, B. and Vavra, D. (2007), ‘Coping With Capital Inflows: Experiences of Selected European Countries’, IMF Working Paper No. 07/190.

Pesaran M. and B. Pesaran (1997): Working with Microfit 4.0 Interactive Economic Analysis, Oxford, Oxford University Press.

Pesaran, M., Y. Shin and R. Smith (1996): ‘Testing for the Existence of a Long- Run Relationship’, Department of Applied Economics Working Paper No. 9622, Cambridge University, also available on http://www.econ.cam.ac.uk/faculty/ pesaran/ (Accessed in January 2007).

Pesaran, M., Y. Shin and R. Smith (1999): ‘Bounds Testing Approaches to the Analysis of Long-run Relationships’, Cambridge Working Papers in Economics, No. 9907, University of Cambridge.

Pesaran, M., Y. Shin and R. Smith (2001): ‘Bounds Testing Approaches to the Analysis of Level Relationships’, Journal of Applied Econometrics, Vol. 16, No. 3, pp. 289-326.

Pesaran, H and Shin, Y (1998): ‘Generalised Impulse Response Analysis in Linear ultivariate Models’, Economics Letters, Elsevier, Vol. 58(1), pp 17-29, January.

Phillips, P. and P .Perron (1988), Testing for a Unit Root in Time Series Regression, Biometrica, 75, 335-46

Rangarajan, C. (1993), Report of the High Level Committee on Balance of Payments, April.

Rai, K. and Bhanumurthy, N. (2004), ‘Determinants of Foreign Institutional Investment in India: The Role of Return, Risk and Inflation’, The Developing Economies, XLII-4, December, 479–93

Reddy, Y.V. (1998), ‘Managing Capital Flows’, RBI Bulletin, December.

Reddy, Y.V. (1999), ‘External Debt Policies in Emerging Economies: New Dimensions’, RBI Bulletin, July.

Reddy, Y.V. (2000), ‘Capital Flows and Self Reliance Redefined’, RBI Bulletin, August.

Reserve Bank of India (2004a), Handbook of Statistics on Indian Economy, RBI: Mumbai.

Reserve Bank of India (2004b), Report on Trend and Progress of Banking in India (various years), RBI: Mumbai.

Ross, L. (2001), ‘International Financial Liberalization and Economic Growth’ Review of International Economics, vol. 9, issue 4, pages 688-702

Sarno, L., Taylor, M. (1999), ‘Moral Hazard, Asset Price Bubbles, Capital Flows, and the East Asian Crisis: The First Tests’, Journal of International Money and Finance, August, 18(4): 637-57.

Taylor, M. and Sarno, L. (1997), ‘Capital Flows to Developing Countries: Long- and Short-Term Determinants’, World Bank Economic Review, 11 (3), September, 451-70

Trivedi, P., and A. Nair (2003), “Determinants of FII Investment Inflow to India.”, Paper presented at the Fifth Annual Conference on Money & Finance in the Indian Economy, held by Indira Gandhi Institute of Development Research, Mumbai, January 30–February 1.

World Bank (2007), ‘Managing Large Capital Inflows’, World Economic Outlook, chapter 3.

Sinha, C. and Pradhan, N. C. (2008), ‘Regional Financial Integration in Asia: Present and Future’, BIS Papers No. 42, October.