Silu Muduli, Shridhar Kumar Dash* Credit rationing arising out of informational asymmetry and lack of collateral is a well-recognised economic constraint in the credit market. These constraints get magnified for small businesses. This paper attempts to capture the dimension of trustworthiness (calculative trust) by designing a multi-period, incentivised payment structure that will induce economic agents to reveal the existence of private information about any projects or true intentions of paying up the credit that is going to fund the project. The model dynamically estimates the collateral needed by taking into account the truthfulness of the borrower. The proposed design is compared with the benchmark model - credit scoring-based model. Randomised simulations are carried out for the ex ante solution for the borrower. We find that the proposed design outperforms from the perspective of lenders when the probability of default of any project is less than 80 per cent. Our simulation result also finds that building trust helps small business owner to significantly reduce the need for collateral. JEL Classification : M21, R51, G21 Keywords : Calculative trust, collateral Introduction Creation of jobs is one of the most important political/economic issues facing developing economies. The progress of Small and Medium Enterprises (SMEs) is imperative for employment growth because, across developing economies, SMEs are a key employment generation sector (Chu, Benzing and McGee, 2007; Lee, 1998; Lin, 1998). This sector grows when entrepreneurs invest in new projects. Retained earnings may not be sufficient to meet the capital needed for growth and therefore additional capital may need to be raised in the form of debt. However, small businesses encounter financial constraints while raising capital to fund their growth (Panda and Dash, 2014; Thampy, 2010). Constraints faced by small businesses are more binding due to the perceived credit risks associated with them. Credit risk can arise from two sources. First, risk arising from the inability of the project to pay back the loan, and, second, risk arising from unwillingness of the business owner to pay back the loan. There is a well developed risk mitigation strategy for a project’s inability to pay back the loan, driven by intermediaries such as credit rating agencies, credit bureaus, and internally-developed scorecards. On the other hand, the risk mitigation strategy with respect to unwillingness of a business owner to pay back the credit is not well developed. This is the grey area in the underwriting processes followed by lending institutions. Willingness to pay back can be traced to trustworthiness of the business owner. This kind of trustworthiness can be visualised as calculative trust as discussed in Lewicki et al., (2006). One can argue that any economic relationship will start with a principal (lending institution) calculating the trustworthiness of the agent (borrower) on the basis of the perceived credit risk associated with dealing with an agent. As the principal deals with the agent over time, set of information with the principal expands, and the trustworthiness of the agent in the eyes of the principal changes. These inter-temporal changes in calculative trust have not been adequately captured in the available literature. Besides, they have not been modelled in a way to understand the risk arising out of an unwillingness to pay back the loan. The inter-temporal dimensions of the perceived credit risk can also be looked at from a perspective of private information available with a business owner. This asymmetry of information between borrower and lender will lead to adverse selection (ex ante), and the creation of a moral hazard (ex post) problem. To deal with the asymmetric information problem, lending institutions will demand collateral from all types of borrowers (including the good ones). Non-availability of sufficient collateral may in turn result in non-availability of credit to the potentially good quality borrower. This is the classical credit rationing problem put forward by Stiglitz and Weiss (1981). The asymmetry of information problem is particularly binding in the case of SMEs, as they also face lack of collateral. Therefore, one can argue that small business owners are likely to face acute credit rationing. This paper develops an incentivised metrics, which induces the small business owner to reveal certain amount of private information so that the lender can assess the risk associated with the borrower’s unwillingness to pay back the loan. The paper does not address the credit risk arising out of genuine risk of failure of the project due to external socio-economic and political circumstances. The paper assumes that these kinds of genuine risks can be taken care of by credit default scores, and pricing of credit. The paper is organised into five sections. Section II provides a review of the literature. Section III discusses the model, the ex ante solution, and simulation results. Section IV provides the ex post solution for the borrower and Section V concludes the paper. Section II
Literature Survey Non-availability of financial resources is a major constraint faced by start-ups and SMEs in developing countries (Cook, 2001; Gray, Cooley and Lutabingwa, 1997; Levy, 1993; Peel and Wilson, 1996). It is perceived that SMEs belong to a high risk credit category and hence this sector finds it difficult to raise debt capital to fund its business growth (Thampy, 2010). Stiglitz and Weiss (1981) showed that credit rationing will happen due to the existence of information asymmetry. The principal and agents have different sets of information about the project for which credit is needed. Though both are rational, they might not have sufficient incentives to work towards a common goal (Akerlof, 1970; Ross, 1973). However, the lender solves the problem of information asymmetry through contract and monitoring (Sahlman, 1990). The purpose of monitoring is to make sure that there is an incentive for compatibility between the borrower and the lender so that the borrower does not take undue risk. The success of the contractual mechanism to reduce the agency risk depends on the completeness of the contract, and its enforcement. However, enforcement of the contract is a challenge, and is costly (Lawton, 2002). In addition to an appropriate contract, and monitoring, the lender can ask for collateral to reduce the risk due to the failure of a funded project. The need for collateral as a means to reduce credit risk depends on the structure of the credit market (Besanko and Thakor, 1987; Bester, 1985). Chen (2006) showed that the riskier borrowers pledge higher collateral than safe borrowers, and Jimenez and Saurina (2004) found evidence that highly collateralised loans have higher probability of default. The literature on the relationship between ex ante demand for collateral and ex post risk associated with the loan is inconclusive. Therefore, taking high amount of collateral may not reduce the credit default ex post. Logically, one can argue that the willingness to pay back plays an important role in assessing the risk associated with any borrower. A borrower who has low pledgeable collateral and is willing to pay back the loan is likely to be a safer borrower in comparison to a borrower with highly pledgeable collateral but with an unwillingness to pay back the loan. An alternative way to addresses the asymmetry of information problem has been looked from the perspective of trust. Das and Teng (1998), Shepherd and Zacharakis (2001), and Vosselman and Van der Meer-Kooistra (2009) argue that the agency risk can be reduced by employing both contractual mechanisms and trust building in a dyadic relationship. Literature on uses of contract and trust can be visualised from three perspectives. First, the presence of a higher trust level will drive lower levels of control and a less stringent contract (Dyer and Singh, 1998). Second, contractual control increases the trust level, hence contractual control and trust are complementary to each other (Leifer and Mills, 1996; Poppo and Zenger, 2002). Third, trust itself is a type of control mechanism, hence both are substitutes (Bradach and Eccles, 1989). Most of the literature on trust, with respect to the asymmetry of information problem, is discussed in the context of the relationship between venture capitalists and entrepreneurship where there is a greater degree of uncertainty. Panda and Dash (2016) studied different stages of entrepreneurial ventures and found evidence for trust-based control by Indian venture capitalists in the early stage of a firm. They also found a combination of trust and control-based risk mitigation methods adopted by the venture capitalists in the late stages of a firm. The role of trust in building mutually beneficial cooperation has been explored in the case of bank-entrepreneur relationships (Saparito et al., 2004). At present, there is a lack of literature looking at trust in the context of both lender’s and borrower’s perspectives. This paper attempts to bring trust, which builds over time, to calculate the need for collateral. This model takes the concept of calculative trust, as discussed in Lewicki et al., (2006), to facilitate trust building between a borrower and a lender. The proposed model is an attempt to mitigate the need for collateral by incentivising the borrower to be trustworthy over time. This model has the objective of reducing credit constraints for individuals (non-wilful defaulters) without the availability of hard information. Since many of the credit institutions demand collateral from borrowers, the trustworthy borrowers face credit constraints. The model suggests a methodology to reduce this credit constraint. The model is discussed in the following section. Section III
The Model A design in the world of information asymmetry is a procedure to nudge the agent to behave in a pre-specified way, without cohesion. The importance of design can be seen in the Vickrey–Clarke–Groves (VCG) mechanism (Vickrey, 1961; Clarke, 1971; Groves, 1973), where the design helps us to address the following twin objectives: (a) the efficient allocation of public goods among agents which (b) forces them to reveal the true value of these public goods. This is possible by appropriately incentivising the agent to reveal the truth. Our model is inspired by the VCG mechanism to incentivise the borrower to reveal private information about the project for which the loan is sought. At the time when a borrower seeks a loan for a project, it pays for the borrower to communicate in a way that will positively influence the lender to decide on giving the credit. For example, the borrower may overestimate the project cash flows to show a favourable picture in support of the project. The lender will suffer when a project with inflated cash flows is provided credit, and ultimately the project fails and the lender suffers losses. The proposed model creates a design where the borrower is disincentivised to inflate the cash flow numbers, and will make an attempt to tell the truth about the cash flow of the project (according to the information available with the borrower). Furthermore, our design incentivises the borrower not to deviate from the ex ante promises. Parameters of the model
The Design Project – i
Ex ante Solution for the Borrower The Proposition-1 helps us to know the ex ante payment schedule of a rational borrower. However, the same rational borrower will minimise ex post αi+1. The ex ante optimisation problem for the borrower will be Using the Lagrangian multiplier method we can solve the above problem. Lagrangian of the optimisation problem is given by: Here ‘λ1’ is the Lagrange multiplier. From the first order conditions, the solution of the above problem will be
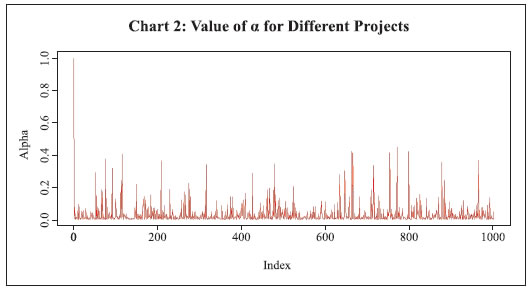
The above optimal solution from our design incentivises the individual to create a payment schedule that decreases over time. Comparison with the Benchmark Model To showcase the value of the proposed design, we have compared the results of our model with a benchmark model. The benchmark case is where a lender provides loans to projects having probability of default less than k. The probability of default is predetermined exogenously. The lender takes collateral before providing the loan. Let the collateral amount be ϕBi (1 + ri)Ti for project i, where ϕ∈ [0,1] which is a policy parameter that decides collateral amount. In case of default, the lender recovers some portion of the loan amount by liquidating the collateral. The liquidating factor is δi, which lies in [0,1]. Then expected profit π for the risk-neutral lender under the benchmark model can be written as: Simulation Result The objective of the simulation is to compare the performance of the proposed model vis-à-vis the benchmark model. The performances are measured in terms of two outcomes. First, profit generated by the lender; and second, total amount of collateral needed as a percentage of total loans given. The simulation is done by coding the model in R software, and has been done for 1000 (n = 1000) projects. Each project has a probability of default, which has been generated randomly from a uniform distribution θi ∼ U[0,1]. The proposed model is applied to generate designed collateral metrics for different projects. The result of the same has been plotted in Chart 1 and Chart 2. 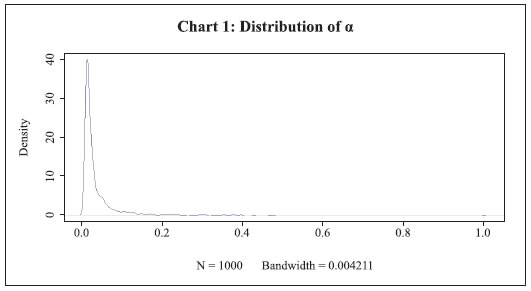
| Table 1: Simulation Result | | E(πModel) − E(πBenchmark) for 1000 Replications (with t-test) | | Loan Amount | k = 0.05 | k = 0.30 | k = 0.5 | k = 0.8 | k = 0.9 | k = 0.99 | | 0–25 lakhs | 12493.85*** | 11348.91*** | 9155.42*** | 2528.79*** | 948.59*** | -1820.46*** | | 0–50 lakhs | 24982.67*** | 22667.89*** | 18299.05*** | 5220.70*** | 1963.96*** | -3713.25*** | | 0–100 lakhs | 49872.13*** | 45475.22*** | 36589.55*** | 10450.63*** | 3784.37*** | -734.23*** | | Notes: *p - value <0.1; **p - value <0.05; *** p - value<0.01. | In the case of the benchmark model we have taken two cases. In the first case, the collateral requirement depends upon the values of θi s, and the amount of collateral required is θiBi(1 + ri)Ti where the amount borrowed is Bi (Table 1). In second case, collateral needed is independent of the default risk of the project (Table 2) and depends on φ, which is a policy parameter as defined before in the model. Liquidating factor δi for collateral of the ith project is generated randomly from a uniform distribution over support [0,1]. For the designed model, we have assumed a random liquidating factor γi which is distributed uniformly over [0,1]. | Table 2: Simulation Result with Policy Parameter ϕ | | E(πModel) − E(πBenchmark) for 1000 Replications (with t-test) | | Policy Parameter | k = 0.05 | k = 0.30 | k = 0.5 | k = 0.8 | k = 0.9 | k = 0.99 | | ϕ=0.01 | 49748.63*** | 45647.11*** | 37804.07*** | 18457.90*** | 9851.07*** | 365.75 *** | | ϕ=0.02 | 50159.46*** | 45590.56*** | 37611.09*** | 18605.34*** | 9689.72*** | 256.72*** | | ϕ=0.03 | 49787.31*** | 45720.78*** | 37709.135*** | 18214.72*** | 9706.17*** | 134.76*** | | ϕ=0.04 | 49885.81*** | 45812.82*** | 37538.95*** | 18109.82*** | 9434.03*** | -15.30** | | ϕ=0.05 | 50231.55*** | 45566.65*** | 37424.77*** | 17930.45*** | 9331.92*** | -152.74*** | | ϕ=0.06 | 50102.85*** | 45813.46*** | 37370.11*** | 17703.19*** | 9204.74*** | -234.56*** | | ϕ=0.07 | 50000.21*** | 45335.13*** | 37255.71*** | 17635.43*** | 9143.52*** | -380.43*** | | ϕ=0.08 | 49958.29*** | 45517.59*** | 37343.81*** | 17412.35*** | 9040.47*** | -500.24*** | | ϕ=0.09 | 49965.63*** | 45271.22*** | 37458.35*** | 17120.41*** | 8971.95*** | -651.28*** | | ϕ=0.1 | 50124.56*** | 45750.08*** | 37210.02*** | 15675.07*** | 8998.34*** | -754.20*** | | ϕ=0.2 | 50278.28*** | 45785.05*** | 36751.19*** | 14185.70*** | 6507.99*** | -39672.21*** | | ϕ=0.3 | 50114.05*** | 45476.90*** | 36716.65*** | 12611.07*** | 4624.84*** | -6356.89*** | | ϕ=0.4 | 50672.44*** | 44952.48*** | 35959.41*** | 10986.27*** | 2470.28*** | -9035.63*** | | ϕ=0.5 | 50057.41*** | 44952.46*** | 35220.93*** | 9489.68*** | 497.98*** | -10476.30*** | | ϕ=0.6 | 50454.53*** | 44770.08*** | 34486.60*** | 7495.72*** | -1731.09*** | -13562.17*** | | ϕ=0.7 | 50409.29*** | 44928.74*** | 33902.88*** | 6289.84*** | -3598.10*** | -16547.25*** | | ϕ=0.8 | 50129.72*** | 44042.05*** | 33995.35*** | 4643.14*** | -5497.62*** | -19042.21*** | | ϕ=0.9 | 50112.10*** | 44062.76*** | 32348.97*** | 3976.87*** | -7861.64*** | -21473.02*** | | ϕ=1 | 50529.24*** | 43792.57*** | 31993.65*** | 3071.992*** | -9744.46*** | -23782.32*** | | Notes: *p - value <0.1; **p - value <0.05; ***p - value<0.01. | The difference E(πModel) − E(πBenchmark Model) has been calculated and the difference between expected profits is tested (one tailed t-test). 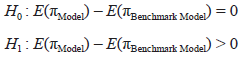 Table 1 shows that the proposed model does better when a project having a probability of default less than 0.9 is accepted by the benchmark model, and the benchmark model will do better for projects with the probability of default greater than 0.9 (which is an unlikely event). Table 2 shows that the proposed model provides better result than the benchmark model for all values of ϕ where k < 0.8. The benchmark model does better when the lender provides loans to very high risk projects, and demands a very high percentage of loan as collateral. The previous two simulations shown in Tables 1 and 2 find the dominance of the proposed model for all projects with a probability of default at 0.8. Table 3 shows the calculated values of collateral needed as a percentage of the total loan amount for the proposed model for different cut-off values of k. We can see that there exists very little difference across the different value of k, which means that the proposed design is independent of the default probability of projects. However, the lender can decide on a cut-off level of k, and after that decide on the collateral need using the proposed model. | Table 3: Collateral Need as a Percentage of Total Borrowing for the Proposed Model | | | | | Loan Amount Limits (in ₹ lakh) | k = 0.05 | k = 0.30 | k = 0.5 | k = 0.8 | k = 0.9 | k = 0.99 | | 0 - 25 | 8.5 | 8.1 | 7.9 | 8.5 | 8.0 | 8.3 | | 0 - 50 | 7.5 | 7.0 | 7.5 | 8.4 | 7.4 | 8.1 | | 0 - 100 | 8.1 | 7.9 | 7.4 | 7.4 | 8.0 | 7.8 | Section IV
Ex post Solution for the Borrower Thus there exists a unique positive solution for λ2 of Eq.7. Since Eq.7 is a non-linear equation, we need computational capabilities to find the optimal payment schedule. We have designed a programme in R to solve for the optimal schedule of the borrower, and the result is shown in Chart 3. As we can see from Chart 3, in case the borrower is unable to pay the first best optimal payment, then the borrower can find the optimal solution for the remaining periods. The optimal schedule shows the borrower has the incentive to pay more in the next period in case the payment was missed in the previous period, which will depend upon the cash flow from the project in the previous period. Thus, the proposed model incentivises the borrower not to default willingly, and pay back the loan as early as possible. Section VI
Conclusion The paper attempts to link mainstream literature on the need for collateral and credit rationing with management literature on trust building over time. The model compares the ex ante payment promise with ex post payment structure for trust building. This is done by creating a design, which incentivises the behaviour of honouring a commitment to a proposed ex ante payment schedule. In the proposed design, a small business owner can improve the creditworthiness over time, and can avail higher amounts of credit with a smaller amount of collateral. The simulation results show that the lending institutions will be able to increase their profit by using the proposed model vis-à-vis the benchmark model. The proposed model will always outperform the benchmark model when the probability of default of a project is less than 80 per cent. Besides, with the help of trust building, a small business owner can bring down collateral requirements to as low as 10 per cent of the total borrowing. The model can be improved by bringing the probability of default into the design, and simulation can be done on real life data of a lending institution.
References Akerlof, G. A. (1970). ‘The market for “lemons”: Quality uncertainty and the market mechanism’, The Quarterly Journal of Economics, 84(3), 488-500. Benmelech, E., and N. K. Bergman (2009). ‘Collateral pricing’, Journal of Financial Economics, 91(3), 339–60. Berger, A. N. et al., (2011). ‘Why do borrowers pledge collateral? New empirical evidence on the role of asymmetric information’, Journal of Financial Intermediation, 20(1), 55–70. Berger, A. N. and G. F. Udell (1990). ‘Collateral, loan quality and bank risk’, Journal of Monetary Economics, 25(1), 21–42. – (1995). ‘Relationship Lending and Lines of Credit in Small Firm Finance’, The Journal of Business, 68(3), 351–381. Besanko, D. and A. V. Thakor (1987). ‘Collateral and rationing: Sorting equilibria in monopolistic and competitive credit markets’, International Economic Review, 28(3), 671–689. Bester, H. (1985). ‘Screening vs. rationing in credit markets with imperfect information’, The American Economic Review, 75(4), 850–855. Bradach, J. L., and R. G. Eccles (1989). ‘Price, authority, and trust: From ideal types to plural forms’, Annual Review of Sociology, 15(1), 97–118. Chen, Y. (2006). ‘Collateral, loan guarantees, and the lender’s incentives to resolve financial distress’, The Quarterly Review of Economics and Finance, 46(1), 1–15. Chu, H. M., C. Benzing and C. McGee (2007). ‘Ghanaian and Kenyan Entrepreneurs: A comparative analysis of their motivations, success characteristics and problems’, Journal of Developmental Entrepreneurship, 12(3), 295–322. Clarke, E. H. (1971). ‘Multipart pricing of public goods’, Public Choice, 11(1), 17–33. Cook, P. (2001). ‘Finance and small and medium-sized enterprise in developing countries’, Journal of Developmental Entrepreneurship, 6(1), 17-40. Das, T. K., & Teng, B. S. (1998). ‘Between trust and control: Developing confidence in partner cooperation in alliances’, Academy of Management Review, 23(3), 491-512. Dyer, J. H., and H. Singh (1998). ‘The relational view: Cooperative strategy and sources of interorganizational competitive advantage’, Academy of Management Review, 23(4), 660–79. Gray, K. R., W. Cooleyand J. Lutabingwa (1997). ‘Small-scale manufacturing in Kenya’, Journal of Small Business Management, 35(1), 66-72. Groves, T. (1973). ‘Incentives in teams’, Econometrica: Journal of the Econometric Society, 41(4), 617–31. Jimenez, G., and J. Saurina (2004). ‘Collateral, type of lender and relationship banking as determinants of credit risk’, Journal of Banking and Finance, 28(9), 2191–2212. Lawton, T. C. (2002). ‘Missing the target: Assessing the role of government in bridging the European equity gap and enhancing economic growth’, Venture Capital: An International Journal of Entrepreneurial Finance, 4(1), 7–23. Lee, C. Y. (1998). ‘Quality management by small manufacturers in Korea: An exploratory study’, Journal of Small Business Management, 36(4), 61-67. Leifer, R., and P. K. Mills (1996). ‘An information processing approach for deciding upon control strategies and reducing control loss in emerging organizations’, Journal of Management, 22(1), 113–137. Levy, B. (1993). ‘Obstacles to developing indigenous small and medium enterprises: An empirical assessment’, The World Bank Economic Review, 7(1), 65–83. Lewicki, R. J., E.C. Tomlinson and N. Gillespie (2006). ‘Models of interpersonal trust development: Theoretical approaches, empirical evidence, and future directions’, Journal of Management, 32(6), 991–1022. Lin, C. (1998). ‘Success factors of small and medium-sized enterprises in Taiwan: An exploratory analysis of cases’, Journal of Small Business Management, 36(4), 43–56. Peel, M. J., and N. Wilson (1996). ‘Working capital and financial management practices in the small firm sector’, International Small Business Journal, 14(2), 52–68. Panda, S., and S. Dash (2014). ‘Constraints faced by entrepreneurs in developing countries: A review and assessment’, World Review of Entrepreneurship, Management and Sustainable Development, 10(4), 405–421. —(2016). ‘Exploring the venture capitalist-entrepreneur relationship: Evidence from India’, Journal of Small Business and Enterprise Development, 23(1), 64–89. Plaut, S. E. (1985). ‘The theory of collateral’, Journal of Banking & Finance, 9(3), 401–19. Poppo, L., and T. Zenger (2002). ‘Do formal contracts and relational governance function as substitutes or complements?’ Strategic Management Journal, 23(8), 707–725. Ross, S. A. (1973). ‘The economic theory of agency: The principal’s problem’, The American Economic Review, 63(2), 134–139. Sahlman, W. A. (1990). ‘The structure and governance of venture-capital organizations’, Journal of Financial Economics, 27(2), 473–521. Saparito, P. A., C. C. Chen and H.J. Sapienza (2004). ‘The role of relational trust in bank-small firm relationships’, Academy of Management Journal, 47(3), 400–410. Shepherd, D. A., and A. Zacharakis (2001). ‘The venture capitalist-entrepreneur relationship: Control, trust and confidence in co-operative behaviour’, Venture Capital: An International Journal of Entrepreneurial Finance, 3(2), 129–149. Stiglitz, J. E., and A. Weiss (1981). ‘Credit rationing in markets with imperfect information’, The American Economic Review, 71(3), 393–410. Thampy, A. (2010). ‘Financing of SME firms in India: Interview with Ranjana Kumar, Former CMD, Indian Bank; Vigilance Commissioner, Central Vigilance Commission’, IIMB Management Review, 22(3), 93–101. Vickrey, W. (1961). ‘Counterspeculation, auctions, and competitive sealed tenders’, The Journal of Finance, 16(1), 8–37. Vosselman, E., and J. Van der Meer-Kooistra (2009). ‘Accounting for control and trust building in inter firm transactional relationships’, Accounting, Organizations and Society, 34(2), 267–283.
|