Sudipta Dutta and Angshuman Hait* Received: April 10, 2024
Accepted: November 7, 2024 Stronger balance sheets of non-financial firms can provide a boost to economic activity while stress in their balance sheets can dampen economic activity and weigh adversely on the banking sector health and overall financial stability. A timely assessment of corporate sector’s financial health, therefore, assumes importance. In this paper, we apply the machine learning (ML) algorithms to analyse corporate health, while experimenting with varying thresholds for several established parameters, such as interest coverage ratio (ICR) and net worth. We also combine ICR and net worth to define a new and more stringent criteria which further enhances the predictive performance of our model. We underline the superiority of the ML model over the predominantly used logistic model. The variable importance scores indicate cash flow and leverage to be the most important predictors of potential corporate stress. JEL Classification: C45, C52, C53, G33 Keywords: Interest coverage ratio, net worth, logistic regression, neural network, extreme gradient boosting Introduction Growing interconnectedness, changing patterns of businesses and consumer preferences can pose threat to corporate sector viability (Blinder, 2013; and Jones, 2023). While the literature associates failure mostly with small-sized or newly established enterprises (Everett and Watson, 1998; Gupta et al., 2013; Honjo, 2020), several large corporates have also failed over the years. There has been an increase in the occurrence of firm insolvencies in the emerging countries in recent years (Vazza et al., 2019). Such failures have the potential to destabilise the financial system, imposing burden on all stakeholders, including investors, lenders, employees and customers. In recent decades, firm debt levels have notably increased in both developed and developing economies (Cortina et al., 2018). The significant increase in the issuance of leverage advances and junk bonds following the Global Financial Crisis (GFC) has resulted in a positive credit cycle (Altman, 2018), apart from a significant surge in loans, particularly in the developing economies (IMF, 2015; and BIS, 2014). While it is the government debt that has primarily increased in developed economies, the debt of non-financial corporate sector has seen a marked rise in major emerging economies like China, Russia and Brazil, particularly during 2011-2017 (Annex 1). Given the growing share of non-financial corporate debt, the International Monetary Fund (IMF) has highlighted the need for its continuous monitoring, especially in the emerging economies, keeping in mind volatile geopolitical risks and post-pandemic spillovers (IMF, 2023). The substantial increase in debt is often seen as a precursor to financial crises in the developing economies (Herwadkar, 2017; and Schularick and Taylor, 2012). Since corporates in developing economies generally secure local currency funding from domestic banks, increased vulnerabilities in these corporates enhance the likelihood of non-performing assets (NPAs) for banks (Atradius Economic Research, 2016; and Lindner and Jung, 2014). This can constrain banks’ ability to extend credit, affecting economic growth. Altman et al. (2017) note that an accurate assessment of corporate stress is essential for banking sector stability. The increased debt burden of corporates can also impede monetary policy transmission. Therefore, creating dependable strategies to assess corporate sector insolvency is critical from both micro (individual firm) and systemic (financial system/economy) perspectives. The predetermination of a firm’s stress requires an assessment of various parameters and scenarios, including its capability to sustain, valuation of bonds having a potential for default, and of credit derivatives and other securities exhibiting credit risk. A predictive model offers insights into buy/sell/hold advises for shares and accounting forecasts provide guidance about sustainability and financial soundness of firms (Jones, 2023). Stress prediction models assist banks in reducing expenses linked to insolvency (Tinoco and Wilson, 2013). Banks depend on internal ratings-based models for their credit evaluation. However, these are not aimed at determining the probability of potential stress in firms (Bandopadhyay, 2006; and Gupta, 2014). Therefore, probabilistic algorithms leveraging state-of-the-art models to identify potentially stressed firms is a useful exercise not just academically but also for banks. Following the ground-breaking work by Beaver (1966) and Altman (1968) on corporate stress prediction, most studies have relied on statistical or econometric models (Sun et al., 2014). Despite the growing use of machine learning (ML) models, their use for corporate stress forecasting has been limited, particularly in the Indian context. In this paper, we build an ML model to forecast the near-term probability of corporate stress in the Indian context. This model can be used by banks to assess financial health and creditworthiness of their corporate borrowers and can also assist in understanding the potential spillover from the corporate sector to the banking system. We utilise interpretable ML techniques, such as variable importance scores to compare the relative significance of the explanatory variables with respect to the best predictive model. This, to some extent, helps in addressing the likely opaqueness of the best predictive ML model. The paper is organised as follows. Section II reviews the literature on this issue. Section III explains the research methodology. Section IV presents the findings of the paper. Section V details the possible extensions of the paper with Section VI giving the concluding observations. Section II
Literature Review II.1 Review of Models Scholars have used different approaches ranging from Linear Discriminant Analysis (LDA) to ML models. II.1.1 Linear Discriminant Models Beaver (1966) was the first to explore firm stress using a ratio-driven univariate discriminant model. His examination of firms’ profiles revealed substantial disparities in the average accounting indicators between insolvent and solvent firms over a five-year period leading up to the firm’s failure. These discrepancies were increasingly apparent as the failure became imminent. Thus, the accounting variables effectively classified the insolvent and solvent enterprises, multiple years prior to the collapse of the insolvent enterprises. Altman (1968), however, identified several drawbacks, including differences in the usefulness of the various ratios and accounting variables. He utilised ratio analysis to calculate the likelihood of bankruptcy for manufacturing companies in the US. The rationale behind ratio analysis was that troubled organisations would exhibit a significantly different ratio than others. Altman created a Z-score, a linear discriminant, categorising companies into either solvent or insolvent, using a linear combination of select ratios that assessed profitability, liquidity, and solvency. The Z-scores successfully detected bankruptcy in multiple cases, offering predictions up to two years in advance of the actual incidence of failure, and accurately identified over 80 per cent of the troubled firms a year before failure. Various scholars subsequently used this approach (Izan, 1984; and Ko, 1982). Jones (1987) highlighted non-conformity of various assumptions, such as multivariate normality and independent error structure in LDA. According to Greene (2008), LDA oversimplified the categorisation of firms as those which will be bankrupt and others without taking into account any other considerations, providing only a binary and not a dynamic probabilistic view. II.1.2 Logit/Probit Models Ohlson (1980) used a logistic regression model (also called logit) for predicting corporate bankruptcy, thus, pioneering its application in this field. Logistic model is distinguished by its improved interpretability and greater flexibility in statistical assumptions as compared to LDA. Ohlson’s methodology encompassed nine elements, including the company’s financial framework, performance metrics, and current solvency. However, scholars noted low efficacy of both LDA and logistic models (Begley et al., 1997). Choe et al. (2002) performed a comparative examination of accounting data from Australia and Korea, following a similar approach. While their findings corroborated earlier studies, they observed that the discrepancies could be ascribed to the economic and industrial situation of a country. Similarly, according to Brigham et al. (1994), the accuracy of stress prediction was influenced by country-specific and industry-specific factors. Zmijewski (1984) utilised a probit model that required normally distributed variables and independent errors, which imposed greater restrictions compared to the logistic model. II.1.3 Hazard Models With LDA, logit and probit having specific drawbacks in adequately handling time-variant structures, the use of hazard models gained acceptance for time-variant structures (Leclere, 2000). Shumway (2001) proposed a Hazard model, where vulnerability to insolvency varied over time, based on the firm’s latest financial information and age, to tackle this issue. Hillegeist et al. (2004) employed a Hazard model to assess the predictive capacity of both accounting and market-oriented factors. They compared Z-Score and O-Score, both made up of accounting ratios. Hill et al. (1996) employed a competing risk approach to investigate financially unwell enterprises that either continued to operate or became bankrupt. Financial stress was identified by looking for entities that experienced negative earnings for a cumulative duration of three years within the sample time frame. Their dynamic model incorporated firm-specific factors like liquidity, profitability, leverage, and size, and macroeconomic factors like unemployment rates. Duffie et al. (2007) also employed a competing risk approach to analyse the nature of the variables converging to their long-run equilibrium value. They combined firm-specific factors, such as return on share, and macroeconomic factors, such as broad market return and treasury rates. They concluded that market-oriented factors may be important for predicting failure. II.1.4 Market-based Models Several studies have mentioned the importance of market-based models in detecting potential business failures. These approaches are commonly classified into two types: structural form models (Merton, 1974) and reduced form models (Jarrow and Turnbull, 1995). Chen and Xu (2018) incorporated market characteristics, such as stock returns, return volatilities, and earnings per share in their stress prediction model. Shumway (2001) showed that combining accounting ratios with stock returns and return variance can predict failure. Hillegeist et al. (2004) employed Black-Scholes-Merton (BSM) model utilising market-based factors. Agarwal and Taffler (2008) compared Z-score model with BSM model and found that the market-based determinants and the accounting ratios were both important. Campbell et al. (2008) noted that attributes, such as capitalisation, P/B ratio, and return volatility indicate a company’s increasing susceptibility to financial difficulties over long periods. Several empirical studies demonstrated that financially troubled enterprises experience a decrease in their surplus returns before ultimately collapsing (Campbell et al., 2008). II.1.5 Machine Learning1 Models Neural network models have less restrictions compared to LDA and logit in terms of the data generating process and model specification (Etheridge and Sriram, 1997). Neural network models iteratively understand the graphical relationships between the variables, going beyond the restrictions of linearity (Zhang et al., 1999). Odom and Sharda (1990) were trailblazers in employing neural network models for the purpose of predicting corporate bankruptcy. They noted that neural network model surpassed LDA in terms of prediction accuracy and exhibited superior robustness and consistency. Multiple studies have demonstrated the neural network model’s exceptional efficacy in generating precise forecasts, outperforming alternative statistical prediction methods (Atiya, 2001; and Pendharkar, 2005). However, there is a competing strand of research indicating that LDA, logit, and neural network demonstrate comparable levels of precision and contain favourable attributes (Altman et al., 1994; Boritz et al., 1995; and O’Leary, 1998). Moreover, Neural network models possess certain limitations, primarily in terms of interpretability, as they are inherently opaque (Cybinski, 2001; and Sun et al., 2011) and prone to overfitting when they mistake noise for a valid relationship (Lawrence et al., 1997). Several researchers have intensively focused on Support Vector Machines2 and showed that when the dataset is small, these outperform other statistical/ML algorithms in terms of prediction accuracy and generalisation (Ding et al., 2008; Erdogan, 2013; and Sun and Li, 2012). Ensemble approaches, which combine many predictors to arrive at an output, show superior prediction accuracy compared to individual classifiers (Sun and Li, 2012; Wang et al., 2011). Bagging and boosting are two popular ensemble methods. Bagging or bootstrap aggregation is an ensemble of parallel classifiers, each of which is built on simple random sampling (with replacement) of datapoints and predictors. Boosting is based on sequentially created classifiers that attempts to build a strong classifier from a sequence of weak classifiers, each of which is built on simple random sampling (with replacement) of predictors. Jones et al. (2017) used a Gradient Boosting model for feature extraction. II.2 Issues with Defining Corporate Stress Researchers have defined stress in various ways due to lack of actual defaults. Failure, as defined by Beaver (1966), is the incapacity of a company to fulfil its financial commitments within the designated timeframe. These conditions include occurrences, such as bankruptcy and bond default, having negative balance in a bank account, or failing to make a preferred stock dividend payment. He focussed primarily on liquidity and cash inflow aspect of firms with both being desirable to avoid stress. Organisations that have cash surplus may obtain more funding and those experiencing negative cash flows may face challenges in meeting their financial commitments. Carmichael (1972) provided a definition of financial hardship of a corporate as a condition marked by inadequate liquidity, equity and excess debt. According to Foster (1986), stress refers to a severe shortage of cash requiring significant operational restructuring. Doumpos et al. (1998) define stress as a situation where a firm’s liabilities transcend its assets, resulting in negative net worth. Ross et al. (1999) provided a comprehensive definition of stress, encompassing different scenarios, such as business failure (the incapacity to repay debts after liquidation), technical bankruptcy (the failure to fulfil contractual obligations to repay both principal and interest), and accounting bankruptcy (negative net worth). According to Lin (2009), financial hardship in a firm refers to the condition where the firm is incapable of meeting its financial obligations promptly. Sun et al. (2014) explained comparative financial stress as comparative decline in financial condition over its lifecycle. Ratings data may not be appropriate to identify stressed companies because ratings may differ across agencies. It is also possible that a firm may be unrated. Furthermore, securities of a given company may carry different ratings. Also, ratings often come with a lag. II.3 Reliance on Accounting Ratios to Predict Stress Accounting ratios, obtained from firms’ financial statements, reveal useful information on the likelihood of corporate insolvency (Libby, 1975; and Zavgren, 1985). Researchers have focused on the following ratios: Cash flow: Beaver (1966) and Altman (1968) revealed that organisations with certain financial structures were at a higher risk of default and potential insolvency than others. Cash flow was identified as an important indicator of imminent insolvency (Heath, 1978; Mesaki, 1998 and Sung et al., 1999). Aziz et al. (1988) identified a significant discrepancy between the operational cash flows of financially sound and stressed companies. Dichev (2021), Gentry et al. (1985), and Jones and Hensher (2004) also found strong evidence in favour of cash flows in forecasting financial hardship. Earnings/Profitability: Profitability ratios reflect the efficiency of a firm and are directly linked to its earning maximisation. Keasy and McGuinness (1990) analysed the association between profitability ratios and business bankruptcy and upheld the usefulness of the former in determining the latter. Liquidity: Liquidity ratios, as defined by Back (2001), measure the firm’s capacity to utilise its current assets to meet current liabilities. Glezakos et al. (2010) and Mensha (1984) observed the utility of these measures in bankruptcy prediction models. Activity: Activity ratios, also known as efficiency ratios, assess the extent to which liquid assets are available to support a company’s sales operations. The higher the ratio, the greater is the ability of the firm to effectively utilise its assets to generate profits and lower is the likelihood of bankruptcy. Leverage: Leverage reflects a firm’s indebtedness and its capacity to meet both immediate and long-term commitments. Mensha (1984) and Ohlson (1980) brought out the role played by leverage ratios in determining financial stress of firms. II.4 Research Gap We use ML models for corporate stress forecasting in the Indian context. ML models have been used for Indian corporate stress forecasting only in a sectoral manner (Selvam et al., 2004 for the cement sector, and Sheela et al., 2012 for the pharmaceutical sector). Only Bapat and Nagale (2014) have established the predictive superiority of neural network models over LDA and logistic regression for listed Indian firms across the spectrum. Sehgal et al. (2021) too study Indian firms but employ a small timeframe without considering the pre-GFC and post-pandemic period. They also use a rigid cut-off of ICR and do not order the predictive variables in terms of their significance to the response variable or use ensemble ML models, as we do in our paper. The current paper tests ML models over logistic regression, the commonly used benchmark. We also experiment with the choice of the proxy response variables using different thresholds for ICR to check if a change in the threshold alters the predictive power of the model. We combine two separate proxy response variables, ICR and net worth, to create a new and more stringent proxy variable. We also utilise feature importance scores to interpret the efficacy of individual predictor variables and address the general criticism of opaqueness associated with ML models. Section III
Methodology III.1 Defining the Response Variable The lack of actual defaults poses a challenge in the empirical analysis of corporate distress. Further, the absence of a specific proxy for stress makes this analysis even more challenging. To tackle this problem, we consider the stress classification given by Lin et al. (2012). They, in turn, refer to the works of Altman (1983) and Ross et al. (1999) where financial hardship is attributed to flow-based and stock-based stress. Flow-based stress occurs when a firm’s cash inflow is inadequate to meet its regular obligations, while stock-based stress occurs when a firm’s total liabilities exceed its assets, leading to negative net worth. This definition is easily implementable for listed companies and also allows users flexibility to play around the ICR threshold. We categorise firms as stressed or non-stressed depending on ICR and net worth values. When the ICR drops below 1, it is taken as a signal of financial stress. Negative net worth also signifies financial stress. To experiment with the cut-off value for ICR, we consider 3 different thresholds for ICR viz., 0.75, 1, and 1.25. We also combine the best predicting ICR threshold and negative net worth to generate a new and more stringent stress criteria. III.2 Choosing the Predictor Variables Various researchers have noted the usefulness of the five factors used in Altman-Z score. Further, Gentry et al. (1985) and Sharma (2001) have noted that jointly considering these ratios with cash flow ratio can enhance the stress predictability. We also include size as an explanatory variable in our model, as past studies are inconclusive about its effect. In all, we consider the ratio of operating cash flow to debt, working capital to assets, market value of equity to book value of liabilities, retained earnings to assets, earnings before interest and taxes (EBIT) to assets, sales to assets, and scaled value of log (market cap) as predictor variables (Table 1). Previous research has focused on forecasting stress one year in advance, while we attempt predicting stress two years in advance. Accordingly, we use the second lag to ensure a reasonable number of data points to train and test the models. III.3 Data and Models We use yearly accounting data on 824 listed companies from 2006 to 2022 from Bloomberg. These firms have no missing data for any of the relevant variables during the sample period. We cover various non-financial sectors, such as IT, energy, manufacturing, healthcare, basic materials, consumer goods, and telecommunications. Market capitalisation of these companies was about Rs. 82 lakh crore as at end-December 2023, one-fourth of the total market capitalisation of all listed firms on the Bombay Stock Exchange. Descriptive statistics of the data are provided at Annex Table A14. | Table 1: List of Predictors | | Sr. No. | Variable | Type | Reference Literature | | 1 | Operating Cash Flow to Debt | Cash flow | Altman (1968), Beaver (1966), Dichev (2021), Gentry et al. (1985) | | 2 | Working Capital to Assets | Liquidity | Back (2001), Glezakos et al. (2010), Mensha (1984) | | 3 | Market Value of Equity to Book Value of Liabilities | Leverage | Mensha (1984), Ohlson (1980) | | 4 | Retained Earnings to Assets | Profitability | Beaver (1966), Keasy and McGuinness (1990), Ohlson (1980), | | 5 | EBIT to Assets | Profitability | Beaver (1966), Keasy and McGuinness (1990), Ohlson (1980), | | 6 | Sales to Assets | Activity | Altman (1968), Beaver (1966), Ohlson (1980) | | 7 | Log (Market Cap) scaled into [0,1] range | Size | Altman (1968), Beaver (1966), Ohlson (1980) | | Source: Authors’ compilation. | The dataset is divided into two parts viz., training and test in 75:25 ratio, as is commonly done in ML-based studies, in accordance with the sequential nature of the data. The training set (2008 to 2016) is utilised to instruct the model, while the test set (2017 to 2019) is employed to assess the model’s predictive capabilities. Also, the data during the COVID-19 period (2020 to 2022) is kept separate to check the efficacy of the best predictive model during this period. Around 6.2 per cent and 2.8 per cent of the firms in the training sample were stressed taking the definitions of ICR < 1 and net worth < 0, respectively (Chart 1). If both criteria were considered, the share came down to 2.2 per cent. Notably, the proportion of stressed firms was high during 2008-2012, after which it fell and then rose sharply during the pandemic. The class imbalance problem3 in our data is addressed using the Synthetic Minority Oversampling Technique (SMOTE) through generation of artificial observations for the minority class. SMOTE helps the ML algorithm to capture important attributes of the minority class, leading to enhanced learning and performance of the model4. We have used SMOTE to ensure around 20 per cent observations are from the minority class in the modified training sample. We have carried out this exercise for each of the separate response variable definitions, viz., ICR < 0.75, ICR < 1, ICR < 1.25, net worth < 0, and the combined definition (ICR < 0.75 and net worth < 0).  We apply various ML models for stress classification, viz., Support Vector Machine, Neural Network, Decision Tree, Random Forest and eXtreme Gradient Boosting, apart from the widely used logistic regression5. III.4 Model Evaluation Metrics and Hyperparameter Tuning All the models are compared based on the following model fitting measures: F1 Score: ML binary classification models use metrics, such as precision and recall to measure model fit. Precision is the ratio of true positives and predicted positives (true positives and false positives), whereas recall is ratio of true positives and actual positives (true positives and false negatives). F1 score, the harmonic mean of precision and recall, weighs the smaller one more. This makes F1 score a better measure than accuracy which only checks the proportion of accurate classifications (Hand et al., 2021). This is an important attribute as there could be cases where false positives are costlier than false negatives, and vice versa. Area Under the Curve (AUC): AUC is the area under the receiver operating characteristic (ROC) curve and is employed as a metric to evaluate the discriminative capability of a model. AUC is used by various ML practitioners across diverse disciplines (Hosmer, Lemeshow, and Sturdivant, 2013). Bradley (1997), Fawcett (2006) and Huang and Ling (2005) recommended utilisation of AUC to evaluate classification algorithms, especially to tackle imbalance problem. ROC curve represents the true positive rate (the accurate classification of healthy companies as healthy) on the y-axis, and the false positive rate (the inaccurate classification of unhealthy companies as healthy) on the x-axis. Higher AUC signifies a stronger ability of the model to identify the troubled companies. Brier Score: Brier Score measures the precision of probabilistic estimations, and acts like a cost function. For binary classifications, it is calculated as the average of the squared terms of the difference between probability estimate and class. Class is binary and takes values 1 and 0 based on event and non-event, respectively. Lower values indicate precise estimations. It is often used to distinguish between two models when the models have similar performance metrics, including accuracy. For each of the ML models, grid search method is followed for hyperparameter finalisation. Grid search method searches for the optimum number of values for the hyperparameters within the range of values specified by the user. By varying the values of various hyperparameters within the user-specified range, different specifications are generated. Each specification is trained on the training set, and the final hyperparameters that optimise a model evaluation metric (maximisation of AUC) are selected. These hyperparameters are used to evaluate the model in the test set (Table A13). Section IV
Empirical Analysis IV.1 Model Evaluation All models are evaluated to predict the stress event based on net worth and various thresholds of ICR for 2- year ahead period using the test set (i.e., 2017 to 2019 and 2020 to 2022). F1 score from the ICR models with different thresholds (Chart 2, Table A1) showcase the superiority of the ML models over logistic regression. eXtreme Gradient Boosting turns out to be the best performing model with more than 10 per cent performance gain over logistic regression across all the three thresholds. Neural network emerges as the close second. We do not witness any overfitting issue as performance in the test set is similar and comparable to the performance in the training set for all the models. AUC score and Brier score from the ICR models with different thresholds (Charts 3 and 4, and Tables A2 and A3) also suggests that all the ML models perform better than logistic regression. eXtreme Gradient Boosting turns out to be the best performing model followed closely by neural network and Support Vector Machine. With a decrease in the cut-off, the model performance improves. This could be because with a decrease in the cut-off, only the worse companies get included in the dataset and they can be easily identified by the models. With consistently superior performance, ML models seem to be more capable of predicting stressed companies over a horizon longer than one year.
The result of net worth models align with the results of the ICR models (Chart 5 and Table A4). eXtreme Gradient Boosting and neural network emerge as the best performing models, closely followed by Support Vector Machine. There is again no evidence of overfitting. Finally, we combine the best performing ICR threshold (ICR < 0.75) condition and net worth < 0 condition to create a more stringent criteria and set this as the new response variable. The result with this new response variable again demonstrates the superiority of the ML models (Chart 6 and Table A5). The models with the combined response variable have higher F1 and AUC scores than the previous models. Furthermore, there is no evidence of overfitting (Tables A8 to A12).
To test the robustness of the results, the model is tested for the COVID-19 period (2020-2022). The results indicate efficacy of the best predictive model (eXtreme Gradient Boosting) despite a slight decline, as evidenced by lower F1 score and AUC, and higher Brier score (Chart 7 and Table A6).
IV.2 Feature Importance Scores The next step is to interpret the efficacy of the predictor variables. Tree-based models provide permutation-based feature importance scores that list the predictor variables in their order of importance. Feature importance scores are based on the change in the model evaluation metric (AUC in our case) when the explanatory variables are dropped one-by-one. The higher the change, the more important is the explanatory variable. This provides greater interpretability, while addressing the general criticism of opaqueness associated with the ML algorithms to some extent. eXtreme Gradient Boosting, a tree-based ensemble, is found out to be the best performing model in all the cases, closely followed by neural network. The superior performance of eXtreme Gradient Boosting may appear surprising, as it is often seen to be superior in tabular datasets (Grinsztajn et al., 2022; and Shwartz-Ziv and Armon, 2022). The feature importance scores from eXtreme Gradient Boosting combined response model reveals cash flow to be the most important predictor for both pre-pandemic and post-pandemic periods (Chart 8 and Table A7). This is consistent with various previous studies (Jones and Hensher, 2004; Mesaki, 1998). Aligning with Mensha (1984) and Ohlson (1980), leverage also turns out to be an important predictor especially in the post-pandemic period, along with retained earnings. The similarity of variable importance scores across both the periods upholds the robustness of the model. 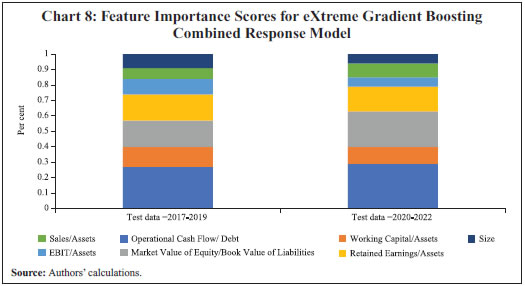 On the whole, the eXtreme Gradient Boosting combined response model emerges as the consistently superior predictive model and is robust across different time periods. Moreover, it also indicates the major predictors, which are again consistent across different time periods. Section V
Conclusion In this paper, we employ several ML models to predict potential financial stress (measured by ICR and Net Worth) for listed Indian companies. The ML models used include Support Vector Machines, neural network, decision tree, and tree-based ensemble methods, such as Random Forests and Gradient Boosting Machines. These models exhibit improved predictive performance when compared to the benchmark logistic regression model. However, ML techniques involve a subjective trade-off between the explainability of the model and its capability to generate precise forecasts. Hence, decision tree-based models are used as these provide a fair degree of interpretability by generating metrics, such as variable importance scores that describe the relative importance of the independent variables. There are, however, certain limitations of our analysis. First, corporates may have the resources to mitigate financial stress predicted by the model, such as through injection of equity or change of leadership/ business strategy. Second, accounting variables can involve ambiguity and can suffer from accounting loopholes. This can influence the predictive power of models based on accounting variables. More stringent measures involving stricter thresholds can be considered. Additional explanatory variables such as other accounting ratios, macroeconomic variables, institutional variables can be considered. Vanilla Recurrent Neural Networks (RNN) or more sophisticated adaptations like Long-Short Term Memory (LSTM) can be employed to incorporate dynamism or recurrence. Cross-sectoral comparisons can also be carried out. Furthermore, stress tests on the predictor variables can be conducted to give better insights into potential financial stress and, therefore, taking corrective actions. References Agarwal, V., & Taffler, R. (2008). Comparing the performance of market-based and accounting based bankruptcy prediction models. Journal of Banking and Finance, 32(8), 1541-1551. https://doi.org/10.1016/j.jbankfin.2007.07.014. Altman, E. I. (1968). Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance, 23(4), 589-609. https://doi.org/10.2307/2978933. Altman, E. I. (2018). A fifty-year retrospective on credit risk models, the Altman Z-score family of models and their applications to financial markets and managerial strategies. Journal of Credit Risk, 14(4), 1–34. DOI: 10.21314/JCR.2018.243. Altman, E. I., Iwanicz-Drozdowska, M., Laitinen, E. K., & Suvas, A. (2017). Financial distress prediction in an international context: a review and empirical analysis of Altman’s Z-score model. Journal of International Financial Management & Accounting, 28(2), 131–171. https://doi.org/10.1111/jifm.12053. Altman, E. I., Marco, G., & Varetto, F. (1994). Corporate distress diagnosis: comparisons using linear discriminant analysis and neural networks (The Italian experience). Journal of Banking and Finance, 18(3), 505-529. https://doi.org/10.1016/0378-4266(94)90007-8. Atiya, A. F. (2001). Bankruptcy Prediction for Credit Risk Using Neural Networks: A Survey and New Results. IEEE Transactions on Neural Networks, 12(4), 929 - 935. DOI: 10.1109/72.935101. Atradius Economic Research. (2016). A closer look at corporate debt in emerging market economies. Report, Atradius Credit Insurance N.V., Amsterdam. Aziz, A., Emanuel, D. C. & Lawson, G. H. (1988). Bankruptcy prediction — an investigation of cash flow based models. Journal of Management Studies, 25(5), 419-437. https://doi.org/10.1111/j.1467-6486.1988.tb00708.x. Back, P. (2001). Testing Liquidity Measures As Bankruptcy Prediction Variables. LTA, 3(01), 301-327. Bandopadhyay, A. (2006). Predicting Probability of Default of Indian Corporate Bonds: Logistic and Z Score Model Approaches. The Journal of Risk Finance, 7(3), 255 – 272. https://doi.org/10.1108/15265940610664942. Bank for International Settlements. (2014). Buoyant yet fragile?. Bank for International Settlements Quarterly Review, Basel. Bank for International Settlements. (2016). Debt securities data base. Report, Bank for International Settlements, Basel. Bapat, V., & Nagale, A. (2014). Comparison of Bankruptcy Prediction Models: Evidence from India. Accounting and Finance Research, 3(4), 1-91. Beaver, W. H. (1966). Financial ratios as predictors of failure. Journal of Accounting Research, 4, 71-111. https://doi.org/10.2307/2490171. Begley, J., Ming, J., & Watts, S. (1997). Bankruptcy classification errors in the 1980s: an empirical analysis of Altman’s and Ohlson’s models. Review of Accounting Studies, 1(4), 267-284. Blinder, A. S. (2013). After the Music Stopped: The Financial Crisis, the Response, and the Work Ahead. Penguin Books, London. Boritz, J. E., Kennedy, D. B., & Albuquerque, A. D. M. E. (1995). Predicting corporate failure using a neural network approach. Intelligent Systems in Accounting, Finance and Management, 4(2), 95-111. https://doi.org/10.1002/j.1099-1174.1995.tb00083.x. Bradley, A. P. (1997). The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition, 30(7), 1145–1159. https://doi.org/10.1016/S0031-3203(96)00142-2 Brigham, E. F., & Gapenski, L. C. (1994). Financial Management: Theory and Practice, 7th ed. Dryden, Orlando, FL. Campbell, J. Y., Hilscher, J., & Szilagyi, J. (2008). In search of distress risk. The Journal of Finance, 63(6), 2899-2939. https://doi.org/10.1111/j.1540-6261.2008.01416.x. Carmichael, D. R. (1972). The Auditor’s Reporting Obligation. Auditing Research Monograph No. 1 (New York: AICPA). Choe, C., & Her, Y. (2002). A Comparative Study of Australian and Korean Accounting Data in Business Failure Prediction Models. Journal of Accounting and Finance, 2002(1), 43-69. Cortina, J. J., Didier, T., & Schmukler, S. L. (2018). Corporate borrowing in emerging markets: fairly long term, but only for a few. No. 8, Research and Policy Briefs, World Bank Group. Cybinski, P. (2001). Description, explanation, prediction-the evolution of bankruptcy studies?. Managerial Finance, 27(4), 29–44. https://doi.org/10.1108/03074350110767123. Dichev, I. D. (2021). Re-orienting the statement of cash flows around cash flows to equity holders. Abacus, 57(3), 407-420. https://doi.org/10.1111/abac.12224. Ding, Y., Song, X., & Zen, Y. (2008). Forecasting financial condition of Chinese listed companies based on support vector machine. Expert Systems with Applications, 34, 3081–3089. doi:10.1016/j.eswa.2007.06.037. Doumpos, M., & Zopounidis, C. (1998). A Multinational Discrimination Method for the Prediction of Financial Distress: The Case of Greece. Multinational Finance Journal, 3(2), 71–101. Duffie, D., Saita, L., & Wang, K. (2007). Multi-Period corporate default prediction with stochastic covariates. Journal of Financial Economics, 83(3), 635-665. https://doi.org/10.1016/j.jfineco.2005.10.011. Erdogan, B. E. (2013). Prediction of bankruptcy using support vector machines: an application to bank bankruptcy. Journal of Statistical Computation and Simulation, 83 (8), 1543–1555. https://doi.org/10.1080/00949655.2012.666550. Etheridge, H. L., & Sriram, R. S. (1997). A comparison of the relative costs of financial distress models: Artificial neural networks, logit and multivariate discriminant analysis. Intelligent Systems in Accounting, Finance and Management, 6(3), 235–248. DOI: 10.1002/(SICI)1099-1174(199709)6:33.0.CO;2-N Everett, J., & Watson, J. (1998). Small Business Failure and External Risk Factors. Small Business Economics, 11(4), 371–390. Fawcett, T. (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27(8), 861–874. https://doi.org/10.1016/j.patrec.2005.10.010 Foster, G. (1986). Financial Statement Analysis, 2nd ed., Prentice Hall, NJ. Gentry, J. A., Newbold, P., & Whitford, D. T. (1985). Classifying bankrupt firms with funds flow components. Journal of Accounting Research (Spring), 23(1), 146-160. https://doi.org/10.2307/2490911. Glezakos, M., Mylonakis, J., & Oikonomou, K. (2010). An Empirical Research on Early Bankruptcy Forecasting Models: Does Logit Analysis Enhance Business Failure Predictability. European Journal of Finance and Banking Research, 3(3), 1-15. Greene, W. (2008). A statistical model for credit scoring. NYU Working Paper No. EC-92-29. Grinsztajn, L., Oyallon, E., & Varoquaux, G. (2022). Why do tree-based models still outperform deep learning on typical tabular data?. 36th Conference on Neural Information Processing Systems (NeurIPS 2022), Track on Datasets and Benchmarks. Gupta, P. D., Guha, S., & Krishnaswami, S. S. (2013). Firm growth and its determinants. Journal of Innovation and Entrepreneurship, 2, 15. https://doi.org/10.1186/2192-5372-2-15. Gupta, V. (2014). An Empirical Analysis of Default Risk for Listed Companies in India: A Comparison of Two Prediction Models. International Journal of Business and Management, 9(9). DOI:10.5539/ijbm.v9n9p223. Hand, D. J., Christen, P., & Kirielle, N. (2021). F*: an interpretable transformation of the F-measure. Machine Learning, 110, 451–456. https://doi.org/10.1007/s10994-021-05964-1 Heath, L. C. (1978). Financial Reporting and the Evaluation of Solvency: Accounting Research Monograph 3. American Institute of Certified Public Accountants, New York. Herwadkar, S. (2017). Corporate leverage in EMEs: did the global financial crisis change the determinants?. BIS Working Paper 681, Bank for International Settlements, Basel. Hill, N. T., Perry, S. E., & Andes, S. (1996). Evaluating firms in financial distress: an event history analysis. Journal of Applied Business Research, 12(3), 60-71. https://doi.org/10.19030/jabr.v12i3.5804. Hillegeist, S. A., Keating, E. K., Cram, D. P., & Lundstedt, K. G. (2004). Assessing the probability of bankruptcy. Review of Accounting Studies, 9, 5-34. https://doi.org/10.1023/B:RAST.0000013627.90884.b7. Honjo, Y. (2000). Business failure of new firms: an empirical analysis using a multiplicative hazards model. International Journal of Industrial Organization, 18(4), 557-574. https://doi.org/10.1016/S0167-7187(98)00035-6. Hosmer, D. W., Lemeshow, S., & Sturdivant, R. X. (2013). Applied logistic regression. John Wiley & Sons. DOI:10.1002/9781118548387. Hu, Y.-C., and Ansell, J. (2007). Measuring retail company performance using credit scoring techniques. European Journal of Operational Research, 183, 1595-1606. Huang, J., Ling, C. X. (2005). Using AUC and accuracy in evaluating learning algorithms. IEEE Transactions on Knowledge and Data Engineering, 17(3), 299–310. https://doi.org/10.1109/TKDE.2005.50 International Monetary Fund. (2023). World Economic Outlook. International Monetary Fund. (2015). Corporate leverage in emerging markets—a concern?. In The October 2015 Global Financial Stability Report (Vulnerabilities, legacies, and policy challenges risks rotating to emerging markets), International Monetary Fund, Washington D.C. Izan, H. Y. (1984). Corporate Distress in Australia. Journal of Banking and Finance, 8(2), 303-320. https://doi.org/10.1016/0378-4266(84)90010-4. Jarrow, R. A., & Turnbull, S. M. (1995). Pricing derivatives on financial securities subject to credit risk. The Journal of Finance, 50(1), 53–85. https://doi.org/10.1111/j.1540-6261.1995.tb05167.x. Jones, F. L. (1987). Current techniques in bankruptcy prediction. Journal of Accounting Literature, 6, 131-164. Jones, S. (2017). Corporate bankruptcy prediction: a high dimensional analysis. Review of Accounting Studies, 22(3), 1366-1422. https://doi.org/10.1007/s11142-017-9407-1. Jones, S. (2023). Distress Risk and Corporate Failure Modelling: The State of the Art. Routledge, Taylor & Francis Group. https://doi.org/10.4324/9781315623221. Jones, S., & Hensher, D. A. (2004). Predicting firm financial distress: a mixed logit model. The Accounting Review, 79(4), 1011-1038. Jones, S., Johnstone, D., & Wilson, R. (2017). Predicting corporate bankruptcy: an evaluation of alternative statistical frameworks. Journal of Business Finance and Accounting, 44(1-2), 3-34. https://doi.org/10.1111/jbfa.12218. Keasy, K., & McGuinness, P. (1990). The Failure of UK Industrial Firms for The Period 1976-1984. Journal of Business Finance & Accounting, 17(1), 119-136. Lawrence, S., Giles, C. L., & Tsoi, A. C. (1997). Lessons in neural network training: Overfitting may be harder than expected. National Conference on Artificial Intelligence, AAAI Press, 540–545. Leclere, M. (2000). The occurrence and timing of events: survival analysis applied to the study of financial distress. Journal of Accounting Literature, 19, 158-189. http://dx.doi.org/10.2139/ssrn.181553. Libby, R. (1975). Accounting Ratios and The prediction of Failure Some Behavioral Evidence. Journal of Accounting Research. https://doi.org/10.2307/2490653. Lin, T. H. (2009). A Cross Model Study of Corporate Financial Distress Prediction in Taiwan: Multiple Discriminant Analysis, Logit, Probit and Neural Networks Models. Neurocomputing, 72(16-18), 3507–3516. https://doi.org/10.1016/j.neucom.2009.02.018. Lin, S. M., Jake, A., & Galina, A. (2012). Predicting default of a small business using different definitions of financial distress. Journal of the Operational Research Society, 63, 539–548. Lindner, P., & Jung, S. E. (2014). Corporate Vulnerabilities in India and Banks’ Loan Performance. IMF Working Paper, 14, 232. Merton, R. (1974). On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance, 29(2), 449-470. https://doi.org/10.1111/j.1540-6261.1974.tb03058.x. Mesaki, M. (1998). Bankruptcy Prediction, Analysis of Cash Now Models. International Review of Business. Moradi, M., Sardasht, M. S., & Ebrahimpour, M. (2012). An Application of Support Vector Machines in Bankruptcy Prediction: Evidence from Iran. World Applied Sciences Journal, 17(6), 710-717. Odom, M. D., & Sharda, R. (1990). A neural network model for bankruptcy prediction. International Joint Conference on Neural Networks, IEEE, 163–168. DOI: 10.1109/IJCNN.1990.137710. Ohlson, J. A. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research, 18(1), 109-131. https://doi.org/10.2307/2490395. Pendharkar, P. C. (2005). A threshold-varying artificial neural network approach for classification and its application to bankruptcy prediction problem. Computers & Operations Research, 32(10), 2561–2582. https://doi.org/10.1016/j.cor.2004.06.023. Reserve Bank of India. (2023). Financial Stability Report. Ross, S. A., Westerfield, R. W., & Jaffe, J. F. (1999). Corporate Finance, Second ed. Homewood IL, Irwin/Mcgraw-Hill. Schularick, M., & Taylor, A. M. (2012). Credit booms gone bust: monetary policy, leverage cycles, and financial crises, 1870–2008. American Economic Review, 102(2), 1029–1061. DOI: 10.1257/aer.102.2.1029. Sehgal, S., Mishra, R. K., Deisting, F., & Vashisht, R. (2021). On the determinants and prediction of corporate financial distress in India. Managerial Finance, 47(10), 1428-1447. Selvam, M., Vanitha, S., & Babu (2004). A study on Financial Health of Cement Industry-Z score Analysis. The Management Accountant, 39(7), 591-593. Senapati, M., & Ghoshal, S. (2016). Modelling Corporate Sector Distress in India. RBI Working Paper Series No. 10. https://www.rbi.org.in/Scripts/PublicationsView.aspx?id=17404. Sharma, D. S. (2001). The Role of Cash Flow Information in Predicting Corporate Failure: The State of The Literature. Managerial Finance, 27(4), 3-28. https://doi.org/10.1108/03074350110767114. Sheela, S. C., & Karthikeyan, K. (2012). Evaluating Financial Health of Pharmaceutical Industry in India Through Z Score Models. International Journal of Social Sciences and Interdisciplinary Research, 1(5), 25-31. Shumway, T. (2001). Forecasting bankruptcy more accurately: a simple hazard model. Journal of Business, 74(1), 101-124. https://doi.org/10.1086/209665. Shwartz-Ziv, R., & Armon, A. (2022). Tabular data: Deep learning is not all you need. Information Fusion, 81, 84-90. https://doi.org/10.1016/j.inffus.2021.11.011. Sun, J., Jia, M.-Y., & Li, H. (2011). AdaBoost ensemble for financial distress prediction: An empirical comparison with data from Chinese listed companies. Expert Systems with Applications, 38(8), 9305–9312. https://doi.org/10.1016/j.eswa.2011.01.042. Sun, J., Li, H., Huang, Q.-H., & He, K.-Y. (2014). Predicting Financial Distress and Corporate Failure: A Review from the State-of-the-art Definitions, Modeling, Sampling, and Featuring Approaches. Knowledge-Based Systems, 5, 41-56. https://doi.org/10.1016/j.knosys.2013.12.006. Sun, J., & Li, H. (2012). Financial distress prediction using support vector machines: Ensemble vs. individual. Applied Soft Computing, 12(8), 2254–2265. https://doi.org/10.1016/j.asoc.2012.03.028. Sung, T. K., Chang N., & Lee, G. (1999). Dynamics of Modeling in Data Mining: Interpretive Approach to Bankruptcy Prediction. Journal of Management Information Systems, 16(1), 63-85. https://doi.org/10.1080/07421222.1999.11518234. Tinoco, M. H., & Wilson, N. (2013). Financial distress and bankruptcy prediction among listed companies using accounting, market and macroeconomic variables. International Review of Financial Analysis, 30(C), 394–419. https://doi.org/10.1016/j.irfa.2013.02.013. Vazza, D., Kraemer, N. W., & Gunter, E. M. (2019). Default, transition, and recovery: 2018 annual global corporate default and rating transition study. Report, S & P Global Ratings. Wang, G. et al. (2011). A comparative assessment of ensemble learning for credit scoring. Expert Systems with Applications, 38(1), 223–230. https://doi.org/10.1016/j.eswa.2010.06.048. Zavgren, C. (1985). Assessing the vulnerability to failure of American industrial firms: a logistic analysis. Journal of Business Finance and Accounting, 12(1), 19-45. https://doi.org/10.1111/j.1468-5957.1985.tb00077.x. Zhang, G. et al. (1999). Artificial neural networks in bankruptcy prediction: General framework and cross-validation analysis. European Journal of Operational Research, 116(1), 16–32. https://doi.org/10.1016/S0377-2217(98)00051-4. Zmijewski, M. E. (1984). Methodological issues related to the estimation of financial distress prediction models. Journal of Accounting Research, 22, 59-82. https://doi.org/10.2307/2490859.
Annex
| Table A1: ICR Models with Different Cut-offs – F1 Score (Test data = 2017-2019) | | Machine Learning Models | ICR<0.75 | ICR<1.0 | ICR<1.25 | | Logistic Regression | 0.64 | 0.63 | 0.61 | | Support Vector Machine | 0.72 | 0.71 | 0.70 | | Neural Network | 0.77 | 0.74 | 0.73 | | Decision Tree | 0.67 | 0.66 | 0.65 | | Random Forest | 0.72 | 0.72 | 0.70 | | eXtreme Gradient Boosting | 0.78 | 0.76 | 0.74 | | Source: Authors’ calculations. |
| Table A2: ICR Models with Different Cut-offs - AUC (Test data = 2017-2019) | | Machine Learning Models | ICR<0.75 | ICR<1.00 | ICR<1.25 | | Logistic Regression | 0.71 | 0.69 | 0.68 | | Support Vector Machine | 0.81 | 0.80 | 0.78 | | Neural Network | 0.84 | 0.82 | 0.81 | | Decision Tree | 0.76 | 0.74 | 0.71 | | Random Forest | 0.81 | 0.79 | 0.76 | | eXtreme Gradient Boosting | 0.85 | 0.83 | 0.82 | | Source: Authors’ calculations. |
| Table A3: ICR Models with Different Cut-offs – Brier Score (Test data = 2017-2019) | | Machine Learning Models | ICR<0.75 | ICR<1.00 | ICR<1.25 | | Logistic Regression | 0.24 | 0.28 | 0.33 | | Support Vector Machine | 0.18 | 0.20 | 0.23 | | Neural Network | 0.14 | 0.18 | 0.20 | | Decision Tree | 0.21 | 0.22 | 0.26 | | Random Forest | 0.17 | 0.20 | 0.24 | | eXtreme Gradient Boosting | 0.11 | 0.13 | 0.16 | | Source: Authors’ calculations. |
| Table A4: Net Worth Models - F1 Score, AUC and Brier Score (Test data = 2017-2019) | | Model | F1 Score | AUC | Brier Score | | Logistic Regression | 0.68 | 0.75 | 0.26 | | Support Vector Machine | 0.78 | 0.86 | 0.17 | | Neural Network | 0.82 | 0.89 | 0.12 | | Decision Tree | 0.70 | 0.78 | 0.23 | | Random Forest | 0.77 | 0.86 | 0.19 | | eXtreme Gradient Boosting | 0.83 | 0.90 | 0.12 | | Source: Authors’ calculations. |
| Table A5: Combined Response Variable - F1 Score, AUC and Brier Score (Test data = 2017-2019) | | Model | F1 Score | AUC | Brier Score | | Logistic Regression | 0.71 | 0.79 | 0.23 | | Support Vector Machine | 0.82 | 0.88 | 0.15 | | Neural Network | 0.85 | 0.92 | 0.09 | | Decision Tree | 0.75 | 0.82 | 0.19 | | Random Forest | 0.80 | 0.86 | 0.16 | | eXtreme Gradient Boosting | 0.86 | 0.92 | 0.08 | | Source: Authors’ calculations. |
| Table A6: Combined Response Variable - F1 Score, AUC and Brier Score (Test data = 2020-2022) | | Model | F1 Score | AUC | Brier Score | | Logistic Regression | 0.67 | 0.74 | 0.25 | | Support Vector Machine | 0.79 | 0.85 | 0.17 | | Neural Network | 0.81 | 0.87 | 0.12 | | Decision Tree | 0.70 | 0.76 | 0.22 | | Random Forest | 0.79 | 0.86 | 0.18 | | eXtreme Gradient Boosting | 0.82 | 0.88 | 0.10 | | Source: Authors’ calculations. |
| Table A7: Feature Importance Scores from eXtreme Gradient Boosting Combined Response Model | | Feature | Scaled Score
(Test data = 2017-2019) | Scaled Score
(Test data = 2020-2022) | | Operational Cash Flow/ Debt | 27% | 29% | | Working Capital/Assets | 13% | 11% | | Market Value of Equity/Book Value of Liabilities | 17% | 23% | | Retained Earnings/Assets | 17% | 16% | | EBIT/Assets | 10% | 6% | | Sales/Assets | 7% | 9% | | Size | 9% | 6% | | Source: Authors’ calculations. |
| Table A8: ICR Models with Different Cut-offs – F1 Score (Train data) | | Machine Learning Models | ICR<0.75 | ICR<1.0 | ICR<1.25 | | Logistic Regression | 0.68 | 0.66 | 0.64 | | Support Vector Machine | 0.77 | 0.75 | 0.74 | | Neural Network | 0.81 | 0.77 | 0.76 | | Decision Tree | 0.71 | 0.69 | 0.68 | | Random Forest | 0.77 | 0.76 | 0.73 | | eXtreme Gradient Boosting | 0.82 | 0.79 | 0.77 | | Source: Authors’ calculations. |
| Table A9: ICR Models with Different Cut-offs - AUC (Train data) | | Machine Learning Models | ICR<0.75 | ICR<1.00 | ICR<1.25 | | Logistic Regression | 0.74 | 0.72 | 0.71 | | Support Vector Machine | 0.86 | 0.83 | 0.81 | | Neural Network | 0.88 | 0.86 | 0.85 | | Decision Tree | 0.79 | 0.77 | 0.74 | | Random Forest | 0.85 | 0.82 | 0.79 | | eXtreme Gradient Boosting | 0.89 | 0.86 | 0.85 | | Source: Authors’ calculations. |
| Table A10: ICR Models with Different Cut-offs – Brier Score (Train data) | | Machine Learning Models | ICR<0.75 | ICR<1.00 | ICR<1.25 | | Logistic Regression | 0.22 | 0.26 | 0.31 | | Support Vector Machine | 0.17 | 0.23 | 0.26 | | Neural Network | 0.13 | 0.16 | 0.19 | | Decision Tree | 0.19 | 0.21 | 0.25 | | Random Forest | 0.14 | 0.19 | 0.21 | | eXtreme Gradient Boosting | 0.10 | 0.12 | 0.14 | | Source: Authors’ calculations. |
| Table A11: Net Worth Models - F1 Score, AUC and Brier Score (Train data) | | Model | F1 Score | AUC | Brier Score | | Logistic Regression | 0.70 | 0.77 | 0.25 | | Support Vector Machine | 0.79 | 0.87 | 0.16 | | Neural Network | 0.84 | 0.90 | 0.10 | | Decision Tree | 0.72 | 0.80 | 0.21 | | Random Forest | 0.78 | 0.88 | 0.17 | | eXtreme Gradient Boosting | 0.84 | 0.92 | 0.10 | | Source: Authors’ calculations. |
| Table A12: Combined Response Variable - F1 Score, AUC and Brier Score (Train data) | | Model | F1 Score | AUC | Brier Score | | Logistic Regression | 0.73 | 0.82 | 0.21 | | Support Vector Machine | 0.83 | 0.89 | 0.14 | | Neural Network | 0.87 | 0.94 | 0.08 | | Decision Tree | 0.77 | 0.85 | 0.17 | | Random Forest | 0.83 | 0.89 | 0.14 | | eXtreme Gradient Boosting | 0.88 | 0.94 | 0.07 | | Source: Authors’ calculations. |
| Table A13: Optimal Hyperparameters | | ML Algorithm | Optimal Hyperparameters | | Support Vector Machine | C = 10.0, Gamma = 0.01, Kernel = polynomial | | Decision Tree | maximum tree depth = 4, minimum samples for a leaf node = 5 | | Random Forest | numbers of trees = 200, maximum tree depth = 3, minimum samples for a leaf node = 5 | | eXtreme Gradient Boosting | numbers of trees = 100, maximum tree depth = 3, minimum samples for a leaf node = 3, learning rate = 0.05 | | Neural Network | activation function = relu, learning rate = 0.01, number of hidden layers = 2, nodes per hidden layer = 3, epochs= 100, initial weights = random, optimisation algorithm = adam, batch size = 50% | | Source: Authors’ calculations. |
| Table A14: Sector Break-up, Average Size, Average Cash Flow of the Sample Companies | | Sr. No. | Sector | No. of Companies | Average Market Cap
(in Billion Rs.) | Average CFO/Debt | | 1 | Manufacturing | 398 | 0.48 | 0.18 | | 2 | Consumer Goods | 91 | 1.66 | 0.42 | | 3 | Constructions, Real Estate | 59 | 2.31 | 0.21 | | 4 | Transport and Communications | 32 | 0.88 | 0.28 | | 5 | Healthcare | 59 | 1.80 | 0.45 | | 6 | IT | 33 | 2.01 | 0.40 | | 7 | Other | 152 | 0.39 | 0.23 | | Source: Authors’ calculations. |
|