Sanjib Bordoloi, Abhiman Das and Ramesh Jangili*
Potential output refers to the highest level of output that can be sustained over the long
term. It is assumed that the existence of a limit of output is due to natural and institutional
constraints. If actual GDP rises and stays above potential output, then (in the absence of
wage and price controls) inflation tends to increase as demand exceeds supply. Likewise, if
output is below potential level, inflation will decelerate as suppliers lower prices to fill their
excess production capacity. The issue of estimating potential output is, therefore, critically
important in understanding the overall Inflationary dynamics of the economy. Against this
background, this paper presents empirical estimates of potential output in India using several
advanced econometric methods based on both monthly and quarterly data. Selection of an
appropriate method is validated against its out-of-sample forecasts as well as from the
spectral density properties. For monthly data, the estimate of the potential growth rate for
the Indian economy is found to converge within the range 9.4 percent to 9.7 percent for most
of the methods. For quarterly data, these methods consistently produce potential output near
to 9.0 percent. The diagnostics of the empirical methodologies suggest that unobserved
component models are most efficient methods for estimation of quarterly potential output.
JEL Classifi cation : E3
Keywords : Potential Output, Output Gap, Growth
Introduction
The overall stance of monetary and credit policy in India is to
provide adequate liquidity to meet genuine credit requirements and
support investment demand in the economy while keeping the price
level within limit. One of the major issues in the formulation of the
monetary policy is to determine whether the economy is operating
above or below its maximum sustainable level. The path of the maximum
sustainable level, commonly known as the potential output, indicates
that level of output that is consistent with stable price level. In other
words, potential output is the maximum output an economy could produce without putting pressure on price level. It is that level of output
at which the aggregate demand and supply in the economy are balanced,
so that, inflation tends to its long-run expected value, if other factors
remain constant. Once potential (capacity) output is estimated, the
capacity utilization rate can be constructed as a ratio of the actual level
of output to the potential output. The capacity utilization generally
conforms to that of a full input point on a production function with the
qualifi cation that capacity represents a realistically sustainable
maximum level of output for a given industry, rather than some higher
unsustainable short term maximum.
Output gap, which is the discrepancy between the actual output
and the potential output, indicates the presence of disequilibrium in
the economy. When the actual output exceed the potential output, i.e.
the output gap becomes positive, the rising demand leads to an
increase in the price level, if temporary supply factors are held
constant. Such instances are seen as a source for Inflationary pressures
and as a signal for the central bank to tighten monetary policy. In
case of a negative output gap, inflation tends to fall. The idea of
potential output is, therefore, essential to capture the process of
inflation dynamics in the economy. However, potential output cannot
be observed directly and needs to be estimated.
The objective of this study is to estimate the potential output for
the Indian economy using various univariate and multivariate
techniques. Both annual and quarterly data of output [Gross Domestic
Product (GDP)] are used to estimate the potential output, both at the
aggregate and at the three prime sector level, viz., agriculture and
allied, industry and services sectors. Selection of the method to
estimate potential output is done through the application of spectral
analysis as well through regression analysis. The method that explains
the larger proportion of spectral mass in the range of business cycle
frequencies (i.e. from 5 quarters to 32 quarters or 15 months to 96
months) is selected for estimation of the potential output. Alternatively,
the estimate of output gap, which explains maximum inflation or is
having minimum root mean square error (RMSE) is selected to
estimate the potential output.
The rest of the paper is organized as follows: a priori the debate
on the use of potential output as a variable for demand pressure is
presented in Section I. Methodological developments, with special
emphasis to recent literature, over a historical perspective are
provided in Section II. Section III reviews a few recent empirical
literatures at the national as well as international level. Empirical
estimates of potential output in India under various methods are
presented in Section IV. Finally, Section V concludes the paper with
a few policy implications.
Section I
Potential Output and inflation : Alternative Views
If the real output grows rapidly in the future, the competition for
scarce productive resources could put upward pressure on wages and
other production costs and ultimately inflation could be raised. Most
economic forecasters believe Inflationary pressures build after
potential output rises above a certain level. Some analysts, however,
claimed that the historical relationship is no longer valid because the
present economies are more open today and hence allowing imported
goods to relieve any shortage of domestic capacity. Inflationary
pressures typically emerge when the overall demand for goods and
services grows faster than the supply, causing a decrease in the amount
of unused productive resources, or economic slack mostly captured
through unemployment rate, which measures unused resources in the
labour market. Inflationary pressures can be judged by comparing the
current capacity utilization rate with an estimated stable inflation rate.
When capacity utilization is at the stable inflation rate, inflation tends
neither to increase nor to decrease. The concept is similar to the natural
rate of unemployment, the unemployment rate for which inflation
neither increases nor decreases, but uses capacity utilization rather
than unemployment as the measure of economic slack.
Some analysts contend that potential output has become a less
dependable indicator of Inflationary pressures. Critics of it believe
that potential output as an inflation indicator tend to over simplify the description of both monetary policy formulation and the Inflationary
process. For example in an article appeared in the Wall Street Journal
on February 14, 1995, it is indicated that monetary policy should not
be guided by using capacity utilization as an indicator of inflation. It
is argued that, in practice, a simple relationship between capacity
utilization and the overall inflation rate may not exist. Influences on
inflation other than resource utilization routinely appear in economic
models. Economic developments abroad and foreign exchange rate
swings can effect domestic inflation directly through changes in
prices of imports and indirectly through competing goods effects on
domestic strategic price setting behavior. Therefore, use of potential
output as a variable indicating demand pressures has its own
limitations.
Section II
A Review of Methodology and Literature
At the outset it may be stated that, though the concept is
theoretically appealing, empirical estimation of potential output is
not straight forward. It has a long history and still remains a topic of
intense debate. Accordingly, the methodology presented here provides
a broad literature review over the developments of nearly five
decades. In particular, we present a synoptic view of various
techniques those are developed since 1960, excluding typical surveybased
measures of capacity variables.
II.1 Early Developments
In an early attempt, Klein (1960) and Klein and Summers (1967),
while working at the Wharton School of Finance and Commerce at
Pennsylvania University, evolved a methodology (which was
subsequently called as “Wharton School Technique”) to estimate the
potential output and capacity utilization rates relating to the US
economy. They defined the capacity of an industry as the maximum
sustainable level of output the industry can attain within a very short
time if the demand for its product were not a constraining factor, when the industry is operating its existing stock of capital at its customary
level of intensity. Subsequently, many other organizations in US, viz.,
the US Department of Commerce, the Bureau of Census, etc., also
started computing potential output series based on the similar
methodology. This method uses time series data only on output and
involves marking of peak levels of output and fitting piece-wise linear
function by joining successive peaks with straight line to estimate the
trend in potential output. For the points before the first peak and after
the last peak, capacity output are estimated by extrapolation of the
fitted curve. The method is also known as trend-through-peaks method.
Despite the simplicity and easiness in implementation, a major
drawback of the method is that it does not establish any links between
output and other economic variables, like actual supplies of inputs,
technological progress, etc., which might have impact on capacity
output. Besides, this approach relies on the existence of recent peaks
in output in order to provide up-to-date/updated estimates of capacity
output. The method, therefore, seems incapable of accounting for
situations arising out of prolonged recession or stagnation.
Interest in measuring the capacity output for the Indian economy
goes back to 1970s (Divatia and Varma, 1970). They concentrated on
the manufacturing industries in India and their estimate of the
capacity variables covering the period 1960-68 was published in the
RBI Bulletin, April, 1970. The methodology suggested by them is
actually a modified version of Wharton School Index in which
monthly data (without seasonal adjustment) instead of quarterly
indices (quarterly average of monthly seasonally adjusted series) was
used. Moreover, in this approach, peak monthly production indices in
a year are taken as potential production for all the months of the year.
Thus the estimated potential production function shows several
discrete jumps at the time points corresponding to changes in the
level of potential production. Though, their method provides a useful
alternative measure of potential utilization, it was severely criticized
mainly on sustainability ground. Moreover, when several firms are
aggregated at the industry level, discrete jump is an unrealistic assumption - a smooth curve as suggested by Wharton School method
may be a more faithful description of the reality in this case. Apart
from these drawbacks, the method also fails to establish any macroeconomic
linkage among various production-related variables.
The National Conference Board (NCB) of the US adopted a
technique for estimating capacity output on the basis of capitaloutput
ratios. The basic assumption made in this approach is that the
lowest capital output ratio corresponds to the capacity output. The
estimates of capacity output are then obtained from capital stock
divided by minimum capital output-ratio. This approach show
signifi cant improvements over Wharton School technique, in a sense
that they make use of at least one important input, capital stock, to
estimate capacity output. However, the reliability of these measures
depends heavily on the accuracy of the measurement of capital,
which in practice is really formidable. Secondly, it ignores various
other important factors, viz., the impact of technological innovations
on output, the impact of labour productivity and labour availability
constraint on output, etc.
Subsequently, Klein and Preston (1967) proposed a sectororiented
production function approach (also known as growth
accounting approach) for estimation of potential output. As per this
approach, the potential output is defined as a full output which could
be produced during any given time if all inputs are fully utilized.
Accordingly, for each sector of the economy, actual output is
expressed as a function of man-hours employed, real utilized capital
and a proxy for technical change. Capacity output is then calculated
by using (i) available man-hours (including fractional unemployment)
in place of man-hours employed and (ii) fully utilized capital (i.e.
available capital) in place of utilized capital in these estimated
production functions (without re-estimating the parameters).
Conceptually, this technique is very sound and is improvement over
the methods stated above in the sense that it correlates output with
related economic variables. However, it has the limitations involved
in estimating the production function. In addition, it is difficult to determine real capital utilized and available man-hours at different
sector/industry level. Moreover, this technique ignores the impact of
total factor productivity on output.
The Organization for Economic Co-operation and Development
(OECD), France, adopted a technique which is considered as
improvement over the production function approach suggested by
Klein and Preston (1967). In first step, the OECD uses actual capital
(instead of using utilized capital as done by Klein and Preston) along
with labour to explain output in the production function. In the second
step, the capacity output are estimated by replacing the employed
labour with the labour force (or potential employment) in the
estimated production function giving due importance to the total
factor productivity (in contrast Klein and Preston ignored the use of
total factor productivity).
II.2 Recent Developments
Since early 1980s, two basic methodologies viz., statistical detrending
and estimation of structural relationships are extensively
used for estimating potential output. In addition, recent years have
witnessed applications of dynamic stochastic general equilibrium
(DSGE) models for estimation. The statistical de-trending method
attempt to separate a time series into permanent (trend) and cyclical
components, whereas, the structural relationships method (basically a
variant of production function approach) attempt to isolate the effects
of structural and cyclical Influences on output, using economic theory.
In practice, both univariate and multivariate approaches are
applied. The univariate approach includes the Beveridge and Nelson,
decomposition (1981), Univariate Unobserved Components (UUC)
model (Watson, 1986; Clark, 1987), Band-Pass (BP) filter (Baxter and
King, 1995) and Hodrick-Prescott (HP) filter (Hodrick and Prescott,
1997). The multivariate approach includes the Production Function,
Structural Vector Auto-regression (SVAR) and Multivariate Unobserved
Components (MUC) model. These methods are discussed below:
II.2.1. The Hodrick-Prescott (HP) filter
The Hodrick-Prescott (HP) filter is a simple statistical smoothing
procedure and has become popular because of its flexibility in
extracting a trend from macro economic data. HP filter fits a trend line
through all the observations of the given series, regardless of any
structural breaks that might have occurred, by making the regression
coefficients themselves vary over time. This is done by finding a trend
output that minimizes a combination of the gap between actual output
and the trend output at any time and the rate of change in trend output
at the last point of time (T).
More precisely for a given actual output Y(t), the trend output
Y*(t) is estimated by minimizing
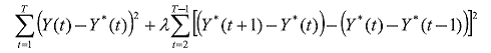 Where λ is a weighting factor that determines the degree of
smoothness of the trend. A low value of λ will produce a trend output
that follows actual output more closely, whereas a high value of λ
reduces sensitivity of the trend output to short term fluctuations in
actual output and in the limit the trend tends to the mean growth rate
for the whole estimation period. Though a lot of subjectivity is
involved in determining the appropriate value of λ depending upon
the nature of the series, it is set to 14400 for monthly data, 1600 for
quarterly data and 100 for annual data. The properties and
shortcomings of the HP filter have been well documented (Harvey
and Jaeger, 1993). The advantage of the HP filter is that stationary is
retained for the output gap over a wide range of smoothing values
and it allows the trend to change over time. HP filter has several
drawbacks, including the arbitrary choices of the smoothing parameter
λ and having high end sample biases.
II.2.2. Beveridge-Nelson (BN) Decomposition
Trend cycle decomposition is motivated by the idea that the log
of aggregate output is usefully thought of as the sum of components that accounts for long term growth and a stationary, transitory
deviation from trend1. Beveridge-Nelson (BN) decomposition is a
detrending method using unobserved components. Output is assumed
to contain unobserved permanent component consisting of a random
walk with drift and temporary component consisting of a stationary
autoregressive process. BN decomposition implies that much of the
variation in output is variation in trend, while the cycle component
is small and noisy. BN decomposition assumes a perfect negative
correlation between trend and cycle innovations that is a property of
the estimated trend and cycle, not the unobserved components.
 To proceed with the decomposition, an ARMA(p,q) is estimated
on the changes in output. Various ARMA models are estimated and
the Schwarz criterion is used to select the best model. Then the series
is decomposed into stationary and trend components using the BN
decomposition technique described above.
II.2.3. Unobserved Components (UC) Model
Harvey op. cit., Clark op. cit. and Harvey and Jaeger (1993)
suggest specifying p=2 and q=0, which allows the cycle process to be
periodic in the sense of having a peak in its spectral density function.
II.2.3.1 Formulation of the problem under Multivariate Unobserved
Components (MUC) setup
In general, estimation of potential output using multivariate
unobserved components model is explored through the Monetary
Condition Index3 (MCI). The MCI captures the general orientation of
the monetary policy affecting the aggregate demand with the objective
to control the inflation rate. Considering the MCI index as an
The model, consisting of the equations from (1) to (6), can be
re-written in its state-space realization and can be estimated by using
the Kalman filter and maximum likelihood.
II.2.4. The Band-Pass (BP) Filter
An ideal low-pass filter removes high-frequency cycles from the
data, whereas an ideal high-pass filter removes low frequencies from
the data and an ideal band-pass filter removes both low and high
frequencies. The Baxter and King (1995) filter is a band-pass filter of
finite order K which is optimal in the sense that it is an approximate
band-pass filter with trend reducing properties and symmetric weights.
The BP filter is designed to pass through components of time series
with fluctuations between 6 and 32 quarters while removing higher
and lower frequencies.
II.2.5. The Production Function Approach
In the view of macro economic analysis, the most important
limitation of all the above methods is that they are largely mechanistic
and bring to bear no information about the structural constraints and
limitations on production through the availability of production
factors or other endogenous Influences. Thus, the above methods
may be inconsistent with what is known or being assumed about the
growth in capital, labour supply or factor productivity or may be
unsustainable because of Inflationary pressures. The production
function approach attempts to overcome these shortcomings while
adjusting also for the limiting infl uence of demand pressure on
employment and inflation.
In its simplest form, this approach postulates a two factor Cobb-
Douglass production function for the business sector with proxy for
technical change:
where Y, L and K are the value added, labour input and capital
stock of the business sector respectively, E is the total factor
productivity, C, δ are constants and α is average labour share
parameter. Lower case letters indicate natural logarithms.
The above production function is estimated at different sub
sector level, for given sample average labour shares. The estimated
residuals from these equations are then smoothed to give measures of trend total factor productivity, e*. The trend total factor
productivity series, e*, is substituted back into the production
function along with actual capital stock, k, and estimates of potential
employment, l*, as:
II.2.6. Structural Vector Autoregression (SVAR) system
The SVAR method uses information from a number of variables
that may be considered to have a high degree of relationship, such as
GDP, capacity utilisation and domestic inflation, to estimate the
potential GDP and output gap. The SVAR methodology utilizes the
relationship between inflation and growth to distinguish between
permanent and transitory movement in output – faster growth with
lower inflation indicates that the economy at that time is operating
below potential, while the emergence of inflation in the face of
growth suggest that output is above potential.
In the present study, the estimate of SVAR is done following the
methodology of Blanchard and Quah (1989), with the exception that
inflation is used in place of the unemployment rate. By imposing
identifying restrictions on the relationship between output and
inflation, the regression residuals are divided into the effects of
supply and demand shocks in each period on output and inflation.
The output gap is then defined as the component of the forecast error
of output attributed to the demand shock – the shortfall or surplus of
output above or below potential due solely to demand side factors.
The SVAR identifies restriction on the long-run effects of shocks
on output and inflation, while the effects of both shocks are left
unconstrained in the short-run4. The restrictions imposed are that
demand shocks affect the long-run price level but not the long-run
output level, while supply shocks can have permanent effects on both
output and price level. Thus a positive supply shock leads to a
permanent increase in the GDP level, while a positive demand shock leads to higher output in the short-run.
II.2.7. Dynamic Stochastic General Equilibrium (DSGE) Approach
Dynamic Stochastic General Equilibrium (DSGE) models
contain many features of the real business cycle literature and allow
for rigidities and imperfections in markets (these are often referred
to as New Keynesian models). These provide more-realistic, yet still
theoretically elegant, representations of the economy, and their
development has been an exciting area of research in macroeconomics
in recent years. Under this approach, potential output is defined as
the level of output that an economy could attain if the inefficiencies
resulting from nominal wage and price rigidities were removed.
That is, if wages and prices were fully flexible. The definition of
potential output as a flexible price equilibrium has much in common
with the more conventional definition. The DSGE definition accords
with the idea that potential output is the level of output at which
inflation tends neither to rise nor to fall. However, the DSGE view
of potential output also has important differences with the earlier
approaches to estimating potential output. For example, in many
DSGE models, potential output can undergo swings over the business
cycle, a result that should not be surprising considering that the early
real business cycle models viewed the business cycle as being
primarily an efficient response to shocks to the economy. In addition,
fiscal policy shocks, changes in households’ preferences with regard
to saving and consumption, changes in preferences about leisure
that affect labour supply, and terms-of-trade shocks can all cause
potential output to fluctuate. In contrast, production function
(growth-accounting) approaches to estimating potential output
generally assume that such shocks have no important effects on
potential output at business-cycle frequencies (Mishkin, 2007). As a
consequence, their estimates typically have smaller fluctuations than
measures of potential output derived from DSGE models, and thus
the output gaps in the current generation of DSGE models tend to be
less variable than conventional measures and can be quite different
for particular periods (Neiss and Nelson, 2005; Edge, Kiley and
Laforte, 2007).
Section III
Recent Empirical Literature
Empirical literature on estimation of potential output is large and
growing rapidly. Most central banks, especially in developed nations,
critically monitor the trends in potential output. Instead of using a
single approach, several approaches are used on a regular basis. Gerlach
and Smets (1999) explored an Multivariate Unobserved Components
(MUC) model to estimate the output gap for the European Monetary
Unit area and found that an increase in the output gap by one percentage
point raises the inflation by 0.2 percent in the next quarter and an one
percentage point increase in the real interest rate reduces next quarter
output gap by approximately 0.1 per cent. The output gap was postulated
as a function of its own lags and to a lagged real interest rate.
Clauss (2000) estimated potential output for the New Zealand
economy through the Structural Vector Autoregression (SVAR)
methodology, under the assumption of that demand-side disturbance
have no long-run effect on output, while the productivity shocks are
assumed to have a permanent effect on output and accordingly
potential output is associated with the productivity shocks. Apart from
the aggregate output, the rate of employment and capacity utilization
were used to estimate the potential output under the SVAR framework.
Cerra and Saxena (2000) applied both UUC and MUC models to
estimate the output gap for Sweden. In the multivariate case, inflation
and unemployment both were applied separately to estimate the output
gap. Scott (2000) estimated the output gap for the New Zealand economy
using MUC model, by assuming a common output gap for Gross
Domestic Product (GDP), unemployment rate and capacity utilization.
For Norway, Bjoruland et al. (2005) compared different
univariate and multivariate methods to estimate the output gap. The
models under the multivariate framework were found to have been
superior to the univariate counterparts in estimating the output gap.
The univariate methods include the HP filter; the BP filter and UUC model, while the multivariate methods include the MUC model and
SVAR. Under the multivariate framework, unemployment rate and/
or inflation were incorporated as the other economic variables.
Llosa and Miller (2005) estimated the output gap for Peru based
on the MUC model through a system of structural equations consisting
of four variables, viz., an index of real monetary conditions, domestic
inflation, imported inflation and inflation expectation. Sarikaya et al.
(2005) estimated the potential output and output gap for the Turkish
economy using MUC approach, through a semi structural model. The
model consists of five equations, consisting of observable variables:
inflation rate, real GDP, real effective exchange rate, real interest rate
based on 3-month Treasury auction and a demand index, constructed
from the Business Tendency Survey.
In the context of India, generally, the HP-filter is being widely
applied to estimate the output gap for the industrial sector [Collen
and Chang (1999), Ray and Chatterjee (2001)]. Donde and Saggar
(1999) applied both HP- filter and UUC model to estimate the
potential output for the industrial sector in India. They further applied
the HP- filter to estimate the potential output for the Indian economy
based on annual observation during 1950-51 to 2000-01.
Section IV
Empirical Estimation of Potential Output in India
Empirical estimates of potential output in India are worked out
based on various approaches as indicated above. However, due to data
limitations, particularly on employment, production function approach
is not attempted. In addition, due to lack of conceptual clarity, estimates
based on DSGE models are not worked out. Empirical estimates are
presented separately using both monthly and quarterly data.
IV.1. Estimates of Potential Output for monthly IIP series
Estimates of potential output for the monthly series are obtained
by using seven alternative methods, consisting of four univariate and three multivariate methods. The univariate methods consist of HP
filter, BP filter, BN-decomposition and UUC methods, while the
multivariate methods includes the MUC (based on MCI) and two
SVAR estimates – based on WPI and MCI, respectively. The sample
covers the period from April 1994 to December 2007. For HP-filter,
the parameter used to smooth the data has been set at 14400, while
for the BP-filter the estimates are obtained within the specified range
between 15 to 60 months.
The estimates of potential growth rate, based on the alternative
methodologies, are presented in Table 1. As can be observed from the
table, the estimate of the potential growth rate for the Indian economy
has been found to have varied in the range from 8.2 percent to 10.2
percent. However, the estimate of 8.2 percent, derived based on the
MUC methodology, seems to be on the lower side compared to the
alternative methodologies. The estimates of the potential growth
rates, based on the HP-filter, BP-filter, UUC and the two SVAR
methodologies are found to have converged, within the range 9.4
percent to 9.7 percent.
Table 1: Estimate of Potential Growth Rates based on monthly data |
Methods |
Potential Growth Rate |
HP |
9.5 |
BP |
9.4 |
BN |
10.2 |
UUC |
9.7 |
MUC |
8.2 |
SVAR - WPI |
9.4 |
SVAR - MCI |
9.5 |
IV.2. Estimates of Potential Output for quarterly GDP series
Estimates of potential output for the quarterly series are obtained
by using eight alternative methods, consisting of four univariate and
four multivariate methods. Apart from using the same set of univariate
and multivariate methods, used to estimate the potential output for
the monthly data, one alternative method of MUC has been used. The two alternative methods of MUC are based on MCI and Capacity
Utilization (CU), where the estimate of CU is based on the survey
conducted by the National Council of Applied Economic Research
(NCAER), New Delhi. The sample covers the period from the first
quarter (April- June) of the financial year 1996-97 to third quarter
(October – December) of the financial year 2007-08. For HP-filter,
the parameter used to smooth the data has been set at 1600, while for
the BP-filter the estimates are obtained within the specified range
between 5 to 24 quarters.
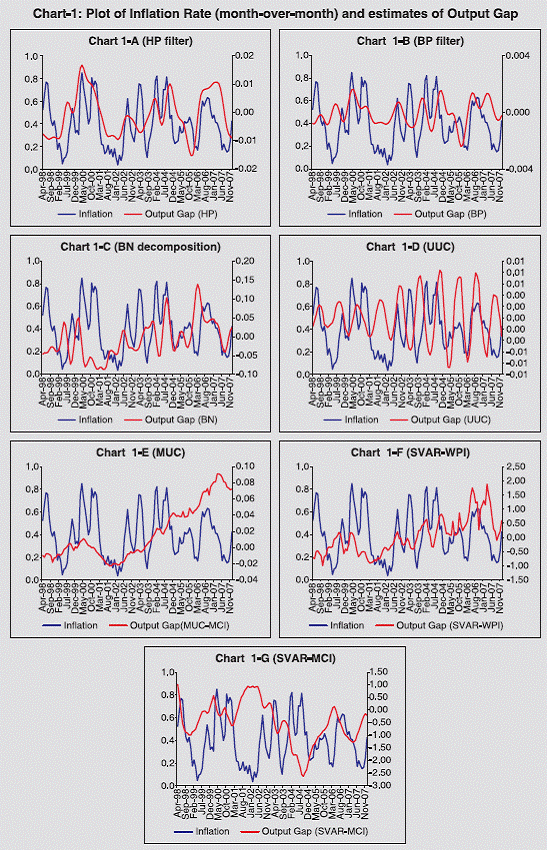
Table 2: Estimate of Potential Growth Rates based on quarterly data |
Methods |
Potential Growth Rate |
HP |
8.5 |
BP |
8.9 |
BN |
9.0 |
UUC |
9.2 |
MUC - Structural |
8.1 |
MUC - CU |
9.5 |
SVAR - WPI |
9.0 |
SVAR - MCI |
9.2 |
The estimates of potential growth rate, based on the eight
alternative methodologies, are presented in Table 2. As can be
observed from the table, the estimate of the potential growth rate for
the Indian economy, based on the GDP, has been found to have varied
in the range from 8.1 percent to 9.5 percent. The estimates of the
potential growth rates, based on the BP-filter, BN decomposition,
UUC and the two SVAR methodologies are found to have concentrated
near 9.0 percent.
IV.3. Selection of the method of estimation of output gap
As mentioned earlier, selection of the method to estimate output
gap can be done by either spectral analysis or regression analysis. In
the regression analysis, one can fit a regression equation and assess
the out-of-sample forecasting performance of the equation based on
certain statistical criteria, like Mean Square Error (MSE), Root Mean
IV.3.1. Selection of the estimate of output gap by regression analysis
To assess the ability and signifi cance of the relationship between
inflation and the estimated output gap, the following equation has
been estimated, as proposed by Coe and McDermott (1997). inflation,
used in the equation, is measured by the changes in the price level
over the previous period as compared to the same period last year.
This measure of inflation helps in assessing the impact of the demand
conditions, reflected through the output gap, on inflation. For the
monthly series, WPI is used to measure the inflation, while GDP
deflator is used to measure the quarterly inflation. B efore empirical
analysis, both the WPI and GDP are seasonally adjusted using the
X-12-ARIMA technique.
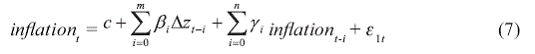 where inflation denotes the inflation rate estimated based on the
monthly WPI or quarterly GDP series. The constant term ‘c’ included
in the equation, indicates the contribution of the non-Inflationary
level of the output gap. The lag length ‘m’ is determined by the
Akaike’s Information Criterion (AIC).
IV.3.2. Selection of the method for estimation of monthly output gap
For selection of the method to estimate output gap by regression
analysis, we divide the full sample period into two sub-samples. The
first sample, known as the in-sample, covering the period from April
1994 to June 2006, is used to estimate the parameters of the equation,
Table 3: Estimate of the equation based on monthly data |
Methods |
R2 |
RMSE |
HP |
0.89 |
0.542 |
BP |
0.88 |
0.565 |
BN |
0.88 |
0.569 |
UUC |
0.86 |
0.611 |
MUC |
0.88 |
0.561 |
SVAR - WPI |
0.88 |
0.578 |
SVAR - MCI |
0.86 |
0.609 |
Table 4 presents the percentages of the spectral mass lying within
the defined range of business cycle of the alternative methods. Data
covers the period from April 1994 to December 2007. As can be
observed from the table, the UUC method, which explains 98.1 per
cent within the business cycle frequency, is the most profi cient at
isolating output gap in the monthly industrial production at the medium term. The BP filter is also relatively profi cient, which explains
95.3 per cent of the total variation. This suggests the selection of UUC
method to estimate the potential output in the monthly IIP series.
Table 4: Percentage of Spectral mass within the business
cycle frequency |
Methods |
Percentage |
HP |
91.7 |
BP |
95.3 |
BN |
69.3 |
UUC |
98.1 |
MUC |
66.9 |
SVAR - WPI |
49.0 |
SVAR - MCI |
46.9 |
IV.3.3. Selection of the method for estimation of quarterly output gap
For selection of the method to estimate quarterly output gap by
regression analysis, we divide the full sample period into in-sample and
out-of-sample, as defined above. The in-sample covers the period from
1996-97:Q1 to 2004-05:Q4, while the out-of-sample covers the period
from 2005-06:Q1 to 2007-08:Q3. The forecasting ability of the output
gap estimates are assessed through out-of-sample RMSE and R2 .
Table 5 presents the out-of-sample RMSE of the alternative
equations based on the estimates of output gap by different
methodologies. From the table it can be observed that, the RMSE is
found to be least in case of UUC, while R2 is found to be marginally
higher in HP compared to UUC. Thus the UUC method can be used
to estimate the potential output in the quarterly GDP series. As the
RMSE of HP is found to be the second least and thus one can apply
HP-filter also to estimate the quarterly potential output.
Table 5: Estimate of the equation based on quarterly data |
Methods |
R2 |
RMSE |
HP |
0.31 |
1.083 |
BP |
0.13 |
1.202 |
BN |
0.18 |
1.151 |
UUC |
0.30 |
1.067 |
MUC - Structural |
0.22 |
1.113 |
MUC - CU |
0.15 |
1.178 |
SVAR - WPI |
0.05 |
1.225 |
SVAR - MCI |
0.06 |
1.218 |
Table 6 presents the percentages of the spectral mass lying within
the business cycle frequency range of the alternative methods. The
sample covers the period from 1996-97:Q1 to 2007-08:Q3. It can be
observed from the table that both UUC and MUC- Structural methods, which explains 99.7 per cent within the business cycle frequency, are
the most profi cient methods to estimate the output gap in the quarterly
GDP. The BP filter is also relatively profi cient explaining 99.6 per
cent of the total variation. This criterion of selection of the method to
estimate output gap suggests UUC or MUC- Structural method as the
most profi cient methods for estimation of potential output in the
quarterly GDP.
Table 6: Percentage of Spectral mass within the business
cycle frequency |
Methods |
Percentage |
HP |
98.7 |
BP |
99.6 |
BN |
94.6 |
UUC |
99.7 |
MUC - Structural |
99.7 |
MUC - CU |
84.0 |
SVAR - WPI |
97.3 |
SVAR - MCI |
32.7 |
Section V
Conclusion
As an economic concept, the definition of potential output is not
unambiguous. The idea of potential output is essential not to capture
the output, but the process of inflation dynamics in the economy. No
statistical measure, however sophisticated, is available which could
reasonably capture the overall demand of the economy, except
potential output. The crux of modern monetary policy making lies
with the understanding of demand process and thus the concept of
potential output is critically important. The path of the maximum
sustainable level indicates that level of output that is consistent with
stable price level. In other words, potential output is the maximum
output an economy could produce without putting pressure on price
level. That is potential output is that level of output at which the
aggregate demand and supply in the economy are balanced, so that,
inflation tends to its long-run expected value, if other factors remains constant. Output gap, which is the discrepancy between the actual
output and the potential output, indicates the presence of
disequilibrium in the economy. When the actual output exceeds the
potential output, i.e. the output gap becomes positive, the rising
demand leads to an increase in the price level, if temporary supply
factors are held constant. In case of a negative output gap, inflation
tends to fall.
In this paper, empirical estimates of potential output in India are
presented using several advanced econometric methods. The selection
of an appropriate method to estimate output gap is done by either
spectral analysis or regression analysis. While in the regression
analysis, the out-of-sample forecasting performance of the regression
equation of potential output explaining inflation is used, in the
spectral analysis, the method that explains the larger proportion of
spectral mass in the range of business cycle frequencies (i.e. from
5-quarters to 32-quarters or 15-months to 96-months) is used.
For monthly data, the estimate of the potential growth rate for
the Indian economy is found to vary in the range from 8.2 percent to
10.2 percent. The estimates of the potential growth rates, based on
the HP-filter, BP-filter, UUC model and the two SVAR methodologies
converge within the range from 9.4 percent to 9.7 percent. For
quarterly data, the estimates of the potential growth rate for the Indian
economy vary in the range from 8.1 percent to 9.5 percent and
methods like BP-filter, BN decomposition, UUC model and the two
SVAR methodologies produce potential output consistently near 9.0
percent. The diagnostics of the empirical methodologies suggest that
UUC or MUC- structural method are most efficient methods for
estimation of quarterly potential output.
Notes
* The authors are Assistant Advisers and Research Officer, respectively, in the
Department of Statistics and Information Management, Mumbai. Views expressed in
this paper are personal views of the authors and not the institution to which they belong.
1 We follow custom in referring stationary, transitory deviation from trend as
the ‘cycle’ even if it is not periodic.
2 Beveridge-Nelson decomposition assumes a perfect negative correlation
between shocks to the trend and cycle, whereas Unobserved Components
model assumes the shocks to trend and cycle are uncorrelated.
3 See Annexure-I for description of MCI and construction of MCI in India.
4 This is against the unrestricted VAR methodology, where the effects of
shocks on all variables are left unconstrained at all horizons.
References
Garner, C.A. (1994): ‘Capacity Utilization and U. S. inflation’, Economic
Review, Fourth Quarter 1994, Federal Reserve Bank of Kansas City.
Batini, N. and Turnbull, K. (2002): ‘A Dynamic Monetary Conditions Index
for the UK’, Journal of Policy Modeling, 24, 257-281.
Baxter, M. and King, R. (1995): ‘Measuring Business Cycles: Approximate
Band-Pass filters for Economic Time Series?’, National Bureau of Economic
Research, Working Paper, No.5022.
Beveridge, S. and Nelson, C. (1981): ‘A new approach to the decomposition
of economic time series into permanent and transitory components with
particular attention to the measurement of business cycle’, Journal of
Monetary Economics, 7, 151- 174.
Bjoruland H., Brubakk L. and Jore A.S. (2005): ‘The output gap in Norway
– a comparison of different methods’, Norgan Bank Economic Bulletin,
76(2), 90- 100.
Blanchard, O.J. and Quah, D. (1989): ‘The Dynamic Effects of Aggregate
Demand and Supply Disturbances’, American Economic Review, 79,
655-673.
Cerra V. and Saxena S.C. (2000): ‘Alternative Methods of Estimating
Potential Output and the Output Gap: An Application to Sweden’, IMF
Working Paper, No. 59.
Clark, P. (1987): ‘The cyclical component of U.S. economic activity’,
Quarterly Journal of Economics, 102(4), 797-814.
Clauss, I. (2000): ‘Estimating potential output for New Zealand: a structural
VAR approach’, Reserve Bank of New Zealand Discussion Paper series, No.3.
Coe, D.T. and McDermott, C.J. (1997): ‘Does the Gap Model Work in
Asia?’, IMF Staff Paper, 44(1), 59- 80.
Collen, T. and Chang, D. (1999): ‘Modeling and Forecasting inflation in
India’, IMF Working Paper, No. 119.
Corrado, C. and Mattey, J. (1997): ‘Capacity Utilization’, The Journal of
Economic Perspectives, Vol. 11, No. 1. (Winter, 1997), 151-167.
Divatia, V.V. and Varma, R. (1970): ‘Index of Potential Production and
Potential Utilization Ratio for the Manufacturing Industries in India’,
Reserve Bank of India Bulletin, April, 1970.
Donde, K. and Saggar, M. (1999): ‘Potential Output and Output Gap: A
Review’, Reserve Bank of India Occasional Papers, 20(3), 439- 467.
Edge, R.M., Kiley, T.K. and Laforte, J.P. (2007): ‘Natural Rate Measures in
an Estimated DSGE Model of the U.S. Economy’, Finance and Economics
Discussion Series, Washington: Board of Governors of the Federal Reserve
System, 2007-8.
Gerlach S. and Smets F. (1999): ‘Output gaps and monetary policy in the
EMU area?’, European Economic Review, 43, 801- 812.
Harvey, A.C. (1985): ‘Trends and Cycles in Macroeconomic Time Series’,
Journal of Business and Economic Statistics, 3, 216-227.
Harvey, A.C. and Jaeger, A. (1993): ‘Detrending, Stylized Facts and the
Business Cycle’, Journal of Applied Econometrics, 8(3), 231- 247.
Hodrick, R.J. and Prescott, E.C. (1997): ‘Postwar U.S. Business Cycles: An
Empirical Investigation’, Journal of Money, Credit and Banking, 29(1),
1-16.
Kannan, R., Sanyal, S. and Bhoi, B.B. (2006): ‘Monetary Conditions Index
for India’, Reserve Bank of India Occasional Papers, 27(3), 57- 86.
Klein, L.R. (1960): ‘Some Theoretical Issues in the Measurement of
Capacity’, Econometrica, 28, 272- 286.
Klein, L.R. and Preston, R.S. (1967): ‘Some New Results in the Measurement
of Capacity Utilization’, American Economic Review, 57, 34-58.
Klein, L.R. and Summer, R. (1967): ‘The Wharton Index of Capacity
Utilization’, Studies in Quantitative Economics, No. 1, Department of
Economics, Wharton School of Finance and Commerce, University of
Pennsylvania.
Llosa G. and Miller S. (2005): ‘Using additional information in estimating
the output gap in Peru: a multivariate unobserved component approach’,
Irving Fisher Committee Bulletin, 20, 167- 182.
Mishkin, F.S. (2007): ‘Estimating Potential Output’, Speech at the
Conference on Price Measurement for Monetary Policy’, Federal Reserve
Bank of Dallas, Dallas, Texas on May 24, 2007.
Neiss, K.S. and Nelson, E. (2005): ‘inflation Dynamics, Marginal Cost, and
the Output Gap: Evidence from Three Countries’, Journal of Money, Credit,
and Banking, 37, 1019-1045.
Ray, P. and Chatterjee, S. (2001): ‘The role of asset prices in Indian inflation
in recent years: some conjectures’, Bank for International Settlement
Papers, No. 8, 131- 150.
Sarikaya C., Ogunc F., Ece D., Curl A.T. and Centinkaya A. (2005):
‘Estimating output gap for the Turkish economy: A semi-structural nonlinear
time series approach’, Irving Fisher Committee Bulletin, 20, 149- 165.
Scott, A. (2000): ‘A multivariate unobserved component model of cyclical
activity’, Reserve Bank of New Zealand Discussion Paper series, No.4.
Watson, M.W. (1986): ‘Univariate Detrending Methods with Stochastic
Trends’, Journal of Monetary Economics, 18, 49- 75.
Annexure-I
Monetary Condition Index
Monetary Condition Index (MCI) is weighted average of changes
in an interest rate and exchange rate relative to their values in a base
period. The weights on the interest rate and exchange rate measure
the relative effects of these variables on the target variables like
aggregate demand or inflation over some period. The extent of
monetary tightening or loosening compared to a previous period may
be judged by observing at the two principal channels of transmission
process – the interest rates and the exchange rates. MCI are computed
to infer the extent of internal and external Influences on the overall
monetary conditions of a country. Algebraically, an MCI is written
as,
Estimation of MCI weights :
Generally, the weights used to compile MCI are derived based
on four alternative methodologies and are described as follows :
(a) Single Equation based :
The relative weights that measure the relative impact of
interest and exchange rates on aggregate demand can be
derived directly by estimating an aggregate demand equation.
The Deutsche Bank derives the weights from an aggregate
demand equation.
(b) Model based :
Weights may also be estimated based on prior estimates of
aggregate demand equations of existing models. The OECD
bases the weights on the MCI from its Interlink Model.
(c) Trade share based :
Weights may also be derived based on the exchange rate
variable as a function of the long-run export to GDP ratio.
The interest rate weight is then calculated as one minus the
exchange rate weight. The weights are interpreted as a crude
relative measure of the effect of the exchange rate on GDP
vis-à-vis the interest rate effect on GDP. J.P. Morgan
constructs a real MCI for the UK based on this methodology.
(d) Multiple equation based :
The weights for the MCI may also be derived based on
unrestricted vector autoregression methodology. MCI
weights are obtained based on the impulse response function
of aggregate output to a shock to each of the interest rate and
exchange rate. Generally, weights are based on the cumulative
average responsiveness to the shocks till the responses die
out. If the variables are found to possess long-run equilibrium
relationship, the weights can be derived based on the impulse
response function under the cointegration framework (Batini
and Turnbull, 2002).
Construction of MCI for India
For the Indian economy, not much work has been done to
construct MCI. Kannan et al (2006) constructed two MCI for the
Indian economy. The first MCI, defined as narrow MCI, was
constructed based on interest rate and exchange rate, while the second
MCI, defined as broad MCI, was constructed by incorporating credit
growth along with the two rates. The weights were derived based on
the single equation estimates of the coefficients of the variables on the overall gross domestic product (GDP) excluding the agriculture
& allied activities and the community, personal and social services.
For our empirical analysis, the MCI is constructed based on the
broad definition as defined in Kannan op cit. The form of the MCI is
as follows,
The weights in the MCI are derived based on the multiple
equation methodology. The interest rate is represented by the average
of the weighted call money rate (CMR), while exchange rate is
represented by the 36-country trade based effective exchange rate of
the Indian Rupee (either nominal (NEER36) or real (REER36)) and
non-food credit (NFC) growth. Both the NEER36 and REER36 are
adjusted by deviation from it base value of 100.
(a) Monthly MCI
For deriving the weights of the monthly MCI, initially, the
variables were tested for order of integration. The widely applied
Augmented Dickey-Fuller (ADF) test was applied to determine the
order of integration. Due to lack of monthly GDP, the Index of Industrial
Production (IIP) is used to represent the output. Empirical results
related to the ADF test are presented in Table A1. From the table, it can
be observed that the annual point-to-point growth in IIP, CMR and
NEER36 are I(0), while, annual point-to-point growth in NFC is I(1).
The sample covers the period from April 1994 to December 2007.
Table A1: Augmented Dickey-Fuller Unit Root Test |
| |
At level |
At first difference |
Remark |
Test Statistic |
Critical Value |
Form of the ADF regression |
Test Statistic |
Critical Value |
Form of the ADF regression |
IIP_g |
-3.095 |
-2.881 |
Constant |
--- |
--- |
--- |
I(0) |
| |
(0.029) |
|
|
|
|
|
|
CMR |
-7.739 |
-3.437 |
Constant, Linear Trend |
--- |
--- |
--- |
I(0) |
| |
(0.000) |
|
|
|
|
|
|
NEER36 |
-3.832 |
-3.437 |
Constant |
--- |
--- |
--- |
I(0) |
| |
(0.003) |
|
|
|
|
|
|
NFC_g |
-0.616 |
-1.943 |
None |
-13.940 |
-1.943 |
None |
I(1) |
| |
(0.449) |
|
|
(0.000) |
|
|
|
Note: Figures in the parentheses indicate the p-values corresponding to the null hypothesis of existence of unit roots. |
To derive the weights for the MCI, we applied the method of
unrestricted vector autoregression using the variables IIP_g, CMR,
NEER36 and the first difference of NFC_g. The impulse responses of
IIP_g to shock of each of the other variables are found to have died
after a period of 30-months. The following graphs present the impulse
response function of IIP_g to the other variables.
(b) Quarterly MCI
For deriving the weights of the quarterly MCI, initially, the
variables were tested for order of integration using ADF. The quarterly
non-agricultural GDP (NAGDP) is used to represent the output.
Empirical results related to the ADF test are presented in Table A-2.
From Table A2, it can be observed that the annual point-to-point
growth in NAGDP and NFC, CMR (adjusted for inflation) and
REER36 are I(0), while, NEER36 is I(1). The sample covers the
period from 1993-94:Q1 to 2007-08:Q3.
To derive the weights for the MCI, we applied the method of
unrestricted vector autoregression using the variables NAGDP_g,
CMR, NFC_g, REER36 and the first difference of NEER36. The
impulse responses of NAGDP_g to shock of each of the other
variables, viz. CMR, NFC_g and REER36 are found to have died after a period of 22-quarters. The following graphs present the
impulse response function of NAGDP_g to the other variables.
Table A2: Augmented Dickey-Fuller Unit Root Test |
| |
At level |
At first difference |
Remark |
Test Statistic |
Critical Value |
Form of the ADF regression |
Test Statistic |
Critical Value |
Form of the ADF regression |
NAGDP_g |
-3.152 |
-2.913 |
Constant |
--- |
--- |
--- |
I(0) |
| |
(0.028) |
|
|
|
|
|
|
CMR |
-3.237 |
-1.946 |
None |
--- |
--- |
--- |
I(0) |
| |
(0.002) |
|
|
|
|
|
|
NEER36 |
-2.358 |
-2.913 |
Constant |
-7.521 |
-1.947 |
None |
I(1) |
| |
(0.158) |
|
|
(0.000) |
|
|
|
REER36 |
-2.322 |
-1.946 |
None |
--- |
--- |
--- |
I(0) |
| |
(0.021) |
|
|
|
|
|
|
NFC_g |
-4.656 |
-3.488 |
Constant, Linear Trend |
--- |
--- |
--- |
I(0) |
| |
(0.002) |
|
|
|
|
|
|
Note: Figures in the parentheses indicate the p-values corresponding to the null hypothesis of existence of unit roots. |
The weights for the MCI are derived as the cumulative average
responsiveness to the shocks till 22-quarters.
|