G V Nadhanael*
The study looks at the recent increase in rural wages and its implication for inflation. Using
Vector Error Correction Model (VECM), the paper empirically tests for the presence of
a wage-price spiral in rural India. The analysis in this paper brings out the following major
inferences: (a) increases in real wages have been a recent phenomenon; (b) during 2000-2007
period, real wages remained constant or declined in rural areas and money wages were largely
responding to inflation; (c) since 2007, wage changes are not explained by changes in prices,
but wages impact prices as increase in real wages has been feeding into cost of production; (d)
MGNREGA wages were higher than market wages for most labour supply states indicating
that the pressure on market wages in those states could be significant; (e) the coverage of
MGNREGA has remained relatively low to exert pressure from demand arising out of cash
transfers and (f) reduced work force participation rates in recent period both on account of
increased participation in education and withdrawal of female work force as well as shift of
labour away from agriculture could have contributed to labour market tightening and increase
in wages. The paper also finds that the recent period increase in wages have not resulted in
convergence of rural wages across states.
JEL : E24, E31
Keywords : Inflation, Wage-price Spiral, Labour Market Tightening
Introduction
Recent developments in rural wages, especially since 2007 has
received much public attention. It has, by now been a well established
fact that in the recent years, wages in rural areas have increased at a
rate higher than the inflation thereby contributing to increase in real
wages (RBI, 2012). This period is also characterised by the introduction
of the Mahatma Gandhi National Rural Employment Guarantee Act
(MGNREGA) which provides 100 days of wage employment for one
member of a family. It has been argued that MGNREGA has been one
of the factors that has contributed to increase in wages (CACP, 2012).
While increase in wages could be beneficial for the rural labourers
from a social welfare point of view, sustained increase in wages have
a number of macroeconomic implications. First, increase in wages,
unaccompanied by productivity increases, could lead to a wage-price
spiral, thereby offsetting the positive impact of initial increase in real
wages on welfare. Second, the ability of public policy, particularly
monetary policy to keep inflation under control could be limited if there
is pressure from wage-price spiral. Also, if increase in wages in one
sector leads to subsequent increase in wages across the economy, the
competitiveness of the economy could be negatively impacted, if such
wage increases are not matched with productivity increases. In this
context, the present study looks at the recent trends in wages to identify
whether there has been a structural break in the trend in wages and what
are the factors that could explain the recent trends. The paper also looks
at the inter-state distribution of wage rates so as to understand whether
the recent increase in wages could exert more persistent pressure or it
could be a one-off shock.
The paper is organised as follows. Following the introduction we
look at the major debates on rural wages in India. This is followed by a
short section on data sources available on rural wages. Trends in rural
wages are analysed in the next section with special focus on the recent
period. This is followed by the analysis of factors that could explain the
recent trends in rural wages. The implications of increase in wages for
inflation are discussed in the next section followed by conclusions.
Section II
Debates on Trends in Rural Wages in India
The studies in rural wage trends in India started in early 1970s
when different scholars tried to analyse the impact of green revolution
on rural standard of living. Agricultural wage change was considered
an indicator of changes in rural standard of living. A pioneering study
on trends in agricultural wages was been undertaken by Bardhan
(1970). He found that real wages in Punjab (including Haryana), Delhi
and Himachal Pradesh and Western Uttar Pradesh did not show any
significant responsiveness to increase in agriculture productivity while in Kerala, agricultural wages increased more than proportionately to
increase in productivity. After analysing the different possible reasons
for this, he came to the conclusion that peasant organisations were the
most important factor determining this increase in the level of wages. He
also concluded that Green Revolution did not have substantial effects
on the rural standard of living because it failed to improve the share of
rural agricultural labourers in total produce. Krishnaji (1971) and Jose
(1974) made use of Agricultural Wages in India (AWI) data to analyse
the movements of money wages and real wages across the States and
over time. Studying wage movements of male agricultural labourers,
they found that money wages were lagging behind rise in prices. They
also concluded that interstate variations in wage rates did widen over
time. The general conclusion of these studies was that Green Revolution
did not have significant impact on the rural standard of living.
Lall (1976) questioned the findings of the earlier studies and
argued that these studies had used AWI data, which is subject to a
lot of methodological problems, and the conclusions will be altered
if one uses National Sample Survey (NSS) data. Again, selection of
mid-1960s as the terminal period in the earlier studies would lead
to misleading conclusions as the impact of green revolution was felt
only after a lag. Sreedhar (1988) also questioned the use of peak
period wage rates as the representative wage rate for the year because
the peak wage for each crop differed and the time of peak rate also
differed in different States.
Another set of studies, which focused on agricultural wage
movements, tried to analyse agricultural wage using a demand and
supply framework. The first major study in this framework was done
by Herdt and Baker (1972). Using AWI data they tried to analyse the
trends in agricultural wages. The study concluded that in India the
supply curve of labour was perfectly elastic while the demand curve
for labour was negatively sloped. This led to a situation in which
increases in the demand for labour pushed up the total employment
rather than increasing the wages. The study thus gave some useful
insights into the problems of the existence of surplus labour. Using the data from NSS surveys Lall (1976) argued that wages did operate
in a demand-supply framework and responded to agricultural growth.
According to the study, decline in rural poverty in the 1970s could be
considered as an indicator for improving the rural standard of living in
India. He argued that the benefits of new technology were shared by
both workers and the producers. Acharya (1989) sought to focus on
the demand and supply aspects of wage determination. To him there
was a decline in real wages during the 1970s, but it was not uniform
across States. Effect of poor monsoon, the inflationary spiral created
by oil shock and Bangladesh war were some of the factors found to be
affecting the agricultural wages in all the States. Coming to the Statespecific factors, immobility of people and resources and differential
productivity were found to be significant in influencing the wage
disparities across States.
Srivastava and Singh (2005) focussed on the rate of growth of
real wages in agricultural sector in pre-reform and post-reform period
and tried to examine the factors affecting the growth in real wages in
the two time periods. The study made use of both rural labour enquiry
(RLE) and AWI data for the analysis. The paper argued that there had
been an increased growth of real wages in agriculture in the pre reform
period. But in the post reform period there was a substantial decline
in the growth rate of agricultural real wages in poor States though
money wages continued to rise. With regard to the determinants of
growth rate, the study found that during the post reform period, the
agricultural growth variables have a lesser effect on the growth of
real wages. Moreover, investments in agriculture have declined. The
growth in wages in post reform period was more from the non-farm
diversification of workforce than from the growth of the sector itself.
Nadhanael (2005) found that agricultural productivity affects growth of
wages over time whereas sectoral distribution of labour force is one of
the key determinants of wage disparities across states.
Recent works on rural wages have focused on the determinants
of sudden increase in rural wages. Gulati et al (2013) found that both
‘push’ and ‘pull’ factors have played a significant role in rising real farm wages. However, the impact of growth variables was much higher
than MGNREGA. Datta et al (2012) found that the MGNREGA wages
remain more or less equal with the rural wages in majority of the states
and therefore, the role of MGNREGA in pushing up market wages may
be limited. Majority of these studies, however, remain silent about the
inflationary implications of this sudden increase in wages.
Section III
Data sources on Rural Wages
There are five different sources from which data on rural wages are
available. They are Agricultural Wages in India (AWI), Rural Labour
Enquiry (RLE), National Sample Survey Organisation (NSSO) surveys
on Employment and Unemployment, Wage Rates in Rural India (WRRI)
and Commission on Agriculture Costs and Prices (CACP) Studies.
Before analysing the trends in rural wages, it would be worthwhile to
summarise the characteristics of the data available from various sources.
The studies in the 1970s and 1980s mostly used the AWI database
as it was the principal data source available. The data is published
by the Directorate of Economics and Statistics in two publications
viz., Agricultural Situation in India (monthly publication) and annual
publication of Agricultural Wages in India. AWI data has, however,
always been used by researchers with a precaution. The data is
collected without adequate conceptual clarity or proper data collection
methodology (Rao, 1972; Himanshu, 2005; and Sharma, 2001; Chavan
and Rajashree, 2006). There is no clear definition of wage or worker
given by AWI data. There is also no well-defined method to convert
kind wages to cash wages.
Rural Labour Enquiry and NSSO are other major sources of data
for agricultural and rural wages in India which are compiled from the
quinquennial employment and unemployment survey conducted by the
NSSO. The data are available only with a gap of five to six years, and
therefore is less suitable for analysing the trends over the period due to
the problems of end-point comparison (Baby, 1996). However, this data
source is considered to be superior to AWI because of its definitional
clarity in concepts used and better sampling methodology (Lall, 1976).
It is to be noted that the concept of wage earnings as defined in RLE/
NSSO is the total sum of earnings received in cash and kind (kind being
converted into money value) on a current weekly status (employment
status of the seven days preceding the date of survey). Earnings in
kind include recurring perquisites like food grains, cooked meals, fuel,
tobacco etc. and also housing, clothes, shoes, bonus etc. which is nonrecurring
perquisites. Rural retail price is used for converting kind
wages into monetary equivalence (Labour Bureau, 2004).
Costs of cultivation studies, which are an extension of earlier
Farm Management Studies, also provide data on wages. The wage
rates obtained through these studies are based on a better sampling
and estimation technique and are considered as superior to other
data sources. However, cost of cultivation studies do not publish the
wage estimates on a regular basis. Moreover, there have been changes
overtime with respect to the number of crops included in the cost of
cultivation studies. Though several independent scholars have tried
to work out the wage rates using the CACP studies, lack of data in a
published format still act as a problem for using these to analyse the
trends in wages.
The Technical Working Group on Rural Retail Prices, set up by
the NSSO in 1976 to revise the estimates of Consumer Price Index
of Agricultural Labourers (CPI-AL) recommended that wage data of
rural workers are to be collected on a continuous basis. Though the data
collection started from 1986-87, due to the questions about the veracity
of data it was not published till 1998. The wage data are collected on a
monthly basis from around 600 villages spread over 66 NSSO defined
agro-climatic regions of different states. From 1998 onwards, the data
is available in the monthly publication of Indian Labour Journal.
The above review of data sources on rural wages in India brings
out the conclusion that the data available from the labour bureau survey
of wage rates in rural India could serve as the appropriate database for
analysis. The only drawback of this data source is that it is not available
for years prior to 1998. Also for our analysis of overall wage movements,
we restrict our focus only on the trends in wages of rural unskilled
labourers (male) on account of the following reasons. First averaging of agricultural wages across occupations may not be meaningful given
the seasonal characteristics of agricultural occupations. Also, unskilled
labourers have the least bargaining power in the rural areas and therefore,
the trends in their wages could be representative of the movements in
subsistence wages. Finally, given the greater inter-connectedness of
rural labour markets, analysis of wage trends in a single occupation
which provides consistent information could be more desirable. For the
present analysis, we use data from June 2000 as the all India aggregated
data for period 1998-2000 is not comparable with the later data due to
changes in methodology of aggregation.
Section IV
Trends in Rural Wages in India
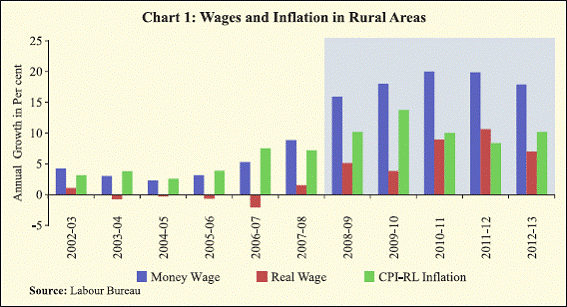
The trends in rural wages since 2000 indicate that there has been
a significant pick-up in the pace of increase in rural wages since 2007-
08. This increase was far in excess of inflation in rural areas in recent
months which led to increase in real wages (Chart 1). This is in contrast
to the previous period of early 2000s when the money wage increases
remained moderate leading to falling real wages during 2003-04 to
2006-07.
There has been an attempt to study the impact of increase in rural
wages on inflation. Empirical estimates based on monthly wages for
rural unskilled labourers and CPI inflation (CPI-Rural Labourers RL), using granger causality indicated that there is a bi-directional
causality between wage inflation and price inflation implying that there
is evidence of a wage-price spiral (RBI Annual Report 2011-12, Box:
II.8).
 This analysis however, presumes that the underlying trend in both
wages and inflation has not undergone any major change over the entire
period of analysis. However, as we saw above, there has been a significant
change in the behaviour of money wages in the recent years. Therefore,
one may have to look for the structural break in the wages and inflation
and then estimate the relationship separately for the different regimes.
Therefore, we first empirically test for the structural break in wage
series. Though there are a number of methods to identify the structural
break within the series, most of the conventional methodologies like the
‘Chow test’ require the researcher to make prior assumptions regarding
the timing of the structural break. Recent work by Bai and Perron
(2003) however, help to estimate and test for structural breaks in a time
series endogenously rather than one based on exogenous information.
This reduces the risk of specification error by the researcher while
making judgement on the timing of structural break. The methodology
considers all possible combination of breaks in the series to select that
point which minimises the sum of squared residuals in the full-sample.
We use the methodology proposed by Bai and Perron (2003) to identify
the structural break in wage data1. From a time series point of view,
though there could be multiple breaks present in the series but we are
interested in the most significant break in the wage series and therefore,
the test was conducted by imposing a restriction of a single structural
break. The result of structural break test is provided in Table 2.
We see that there is a significant break in the money wage growth
since July 2007, a comparison of the coefficient of time (growth rate as
the specification is log linear) is almost five times higher in the second
period as compared to the first. It may noted that this is the period of
large scale implementation of MGNREGA which could be a regime
change in terms of the overall rural labour market. Therefore, analysing the wage-price linkage in these two periods in a combined way may
lead to distorted results as these two periods are characterised by two
distinct regimes.
Table 2: Test for Structural Break in Money Wage Growth |
Dependent Variable: Log of Money Wage
Sequential F-statistic determined breaks: 1 |
Break Test |
F-statistic |
Scaled F-statistic |
Critical Value** |
|
0 vs. 1 * |
8024.672 |
16049.34 |
14.34 |
* Significant at the 0.01 level.
** Bai-Perron (2003) critical values. |
| Break dates: 2007M07 |
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
2000M07 - 2007M06 |
C |
3.892824 |
0.003640 |
1069.450 |
0.0000 |
@TREND |
0.002910 |
5.21E-05 |
55.83045 |
0.0000 |
2007M07 - 2012M11 -- 65 obs |
C |
2.656859 |
0.010815 |
245.6573 |
0.0000 |
@TREND |
0.014381 |
7.66E-05 |
187.8268 |
0.0000 |
The earlier study has used granger causality test to see the link
between wages and inflation. However, the granger causality is usually
conducted in a stationary series by differencing the non-stationary series.
This entails a significant loss of information. Moreover, if the series are
co-integrated in levels, the granger causality on differenced series may
not represent the underlying long-term relation between the variables.
In this context, we look at the wages and prices (as represented by price
index) at levels to see whether they exhibit stable relationships over the
two different regimes.
Section V
Estimation of Wage-Price Linkage
The approach to empirical estimation in the paper for understanding
the link between wages and inflation follows the cointegration analysis
by estimating long-run relationship between the variables and the shortrun
dynamics employing vector error correction model (VECM). First, we test for unit roots to identify the level of integration of the variables
and see whether the variables are integrated of the same order. Then we
proceed to cointegration tests to see the long-run relationships between
wages and prices. Then, the short-run dynamics are analysed by
estimating a VECM to check for the presence of stability of relationship
between the variables. Finally we also look at the block exogeneity
tests to see the direction of relationship between wages and prices. We
attempt estimation over the two distinct periods as identified in the
analysis of structural break.
The unit root tests indicate that the variables log of money wages
(allindia_lmw) and log of CPI-rural labourers price index (allindia_lrl)
are non-stationary at levels and stationary at first difference (Table 3).
Given that the variables are non-stationary at levels and stationary
at first differences, they are integrated of the order 1. This would help
us to test for whether there exists a long-run relationship between the
variables. This is done using Johansen’s cointegration tests. The lag
length was selected to be two based on the Schwarz information criteria
(SIC), given the small sample size for both the periods. The results of
the cointegration tests are given in Annex 1, which indicate the presence
of one co-integrating vector in both the periods under observation.
Given that there is only one co-integrating relationship in both the
periods, the specification of the long-run relation has to take into account
the nature of endogeneity of the variables. The block exogeneity tests are
conducted to identify which variable is exogenous and the specification is formulated appropriately. The results of Wald exogeneity tests for
both the periods are presented in Annex 2.
Table 3: Unit Root Tests |
Variable (X) |
Augmented Dickey Fuller (ADF) |
Philips Perron (PP) |
Log X |
ΔLog X |
Log X |
ΔLog X |
2000m7 to 2007m6 |
AllIndia_MW |
0.76 |
-9.61** |
0.92 |
-9.60** |
AllIndia_RL |
0.34 |
-4.13** |
-0.30 |
-4.23** |
2007m7 to 2012m11 |
AllIndia_MW |
0.45 |
-9.98** |
0.49 |
-9.90** |
AllIndia_RL |
1.21 |
-5.27** |
1.66 |
-5.29** |
Notes: **denote significance at 1% level. Lag length for ADF test was decided on the basis of SIC. |
The block exogeneity tests indicate that the long-run relationship
in the first period could be specified as one where money wages is the
dependant variable and CPI-RL as the explanatory variable. In the
second period, the relationship reverses and CPI-RL turn out to be the
dependant variable and money wage turn out to be the explanatory
variable. The specification and estimated results both for the cointegrating
equation and the error correction equation are given below.
The lag length for short run equation was selected on the basis of SIC.
  The results indicate that the first period was characterised by money
wages adjusting to prices. The elasticity of money wages to prices
remain above 0.9 indicating that wages were almost identically getting
adjusted to price level changes, keeping the real wages constant. If real
wages remain constant, the scope of wages feeding into inflation and
generating a wage-price spiral is limited. Any disturbance in the longterm
relationship was corrected within a short period of time as evident
from a high negative error correction term in the short run equation.
In the second period, wages become a determinant of inflation in
the long-term relationship. This could be possible as there has been a
significant increase in real wages in the recent period. The wages could
have been influenced by a host of factors. Increase in real wages could
lead to further inflation as wage cost push up costs of production and
thereby lead to further increase in prices. Also wages could push up
demand in rural areas thereby leading to pressure on prices from the
demand side. The error correction term in the short run equation for
the second period has the desirable sign but has a very low value and
significant only at about 14 per cent.
Even though we do not find evidence of relationship running from
prices to wages during the second period, the Government has indexed
MGNREGA wages to CPI-AL, from January 2011which could translate
to further wage-price spiral if market wages move in line with MGNREGA
wages. Thereby a risk of wage-price spiral cannot be ruled out.
Section VI
What explains increasing wages?
Though MGNREGA is seen as one of the factors responsible for
pushing up wage levels, its impact is conditional on whether the current
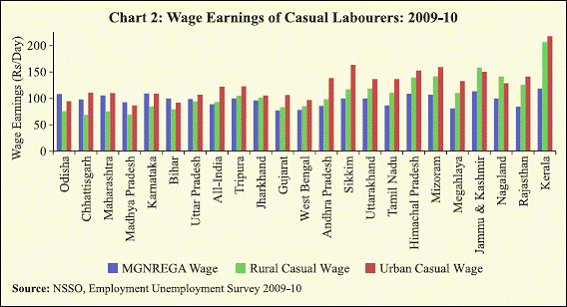
market wages are below or above to the wage rates offered under MGNREGA. It is found that in all the major labour supplying states
(Odisha, Chhattisgarh, Maharashtra, Madhya Pradesh, Bihar and Uttar
Pradesh), the wages received under MGNREGA were higher than the
wages received in rural labour market (Chart 2). Therefore this could
act as a source of pressure as wages could catch up with MGNREGA
wage levels. Even in states where the MGNREGA wage is lower than
the market wages, there could be pressure on market wages if labourers
raise their reservation wages with the introduction of MGNREGA as the
opportunity cost of not getting employment declines. Also, if the market
wage is set as a mark-up over MGNREGA wage, it could influence
the overall wage structure. Also, as the major labour supplying states
have MGNREGA wages higher than market wages, it could slowdown
migration and thereby influence the wage rates in these states. Further
empirical evidence, however, is called for before ascertaining claims on
these grounds.
 MGNREGA could have provided a floor to overall rural wages
and pushed up costs and therefore adding to inflation but the direct
impact of MGNREGA in terms of additional demand may be limited.
This is because the coverage of MGNREGA so far has not been
significant enough to exert major pressure from demand arising out of
cash transfers. Overall at the all India level, only 24.2 per cent of the
families in rural areas received MGNREGA job and even among them
the average number of days of employment is only 37 during 2009-10 (Chart 3). It is seen that in most states, the number of families covered
under MGNREGA is low (less than 50 per cent of rural families) and
the number of days of employment under MGNREGA is also much
lower than the offer of 100 days of employment.
 Apart from the impact of higher inflation and institutional factors
such as MGNREGA on wages, another factor which could have
influenced the overall wage structure in the rural areas in the recent
period is the trends in work force participation rates (WPR). It has
been found that there has been a significant decline in work force
participation among women in most age groups (Chart 4a&b). Among
men, though overall work participation remains almost stable, within
the age group of 15-24 there is a significant fall in WPR. Improved
educational facilities could explain the withdrawal of young population
from work force while decline in female work force participation
could be part of the overall development process where with economic
development; there is a decline in female work force participation
initially before increasing again (the ‘U’ shaped pattern as referred to
in the economic theory). It is also recognised that declining work force
participation among women could also be an effect of increasing wages
(and therefore increasing welfare) and therefore it would be difficult to
establish a one way relationship between increasing wages and work
force participation.
 A decline in work participation rate need not lead to a tightening
in labour market, if the total population is increasing. However, labour
marker tightening could be significant if along with decline in work
force participation rate there is a sectoral shift in employment. Recent
evidence in the Indian case indicates that, there has been a decline in
absolute number of workers employed in agriculture with construction
and services segment attracting more workers out of agriculture
(Chart 5). This could have been another additional factor leading to
increase in rural wages.
Section VII
Has wages converged in the recent period?
As there has been a significant increase in rural wages since 2007,
one critical aspect could be whether this period is also associated
with convergence of wage rates across different states. Given that the
MGNREGA provides near-uniform wage rates across the states, the low
wage states are expected to have a larger pressure from MGNREGA
scheme on market wages as compared to the high wage states. On the
other hand, if the increase in wages is driven by a reduction in labour
supply, or that the market wage is set as a mark-up over the statutory
wage, the pressure on wages could be similar in different states.
Therefore, identifying whether the wages have converged across states
in the recent period could provide important insights into whether the
pressure from wages could be temporary or more persistent.
The co-efficient of variation of wages across 20 major states for the
period under study is plotted in Chart 6. The chart indicate an increase
in variability since 2007 which could indicate that the convergence of
wage rates did not occur during the period of high wage inflation.
Following the convergence literature in economic growth, we
test for wage convergence across states. Two common ways to assess
convergence in the literature is Sigma (σ) convergence and Beta (β) convergence. Under σ convergence, if the measure of dispersion of
wage across regions declines over time, it could be concluded that the
wages are converging and vice-versa. The empirical estimation of σ
convergence could be attempted by regressing the measure of variation
(co-efficient of variation in the present case) over time. A positive and
significant coefficient for time variable (t) would imply divergence and
negative and significant coefficient for t would denote divergence. The
estimated results are:
CV_Wage = 39.9** - 0.018**t (period 2000m7 to 2007m6)
CV_Wage = 30.65** + 0.062**t (period 2007m7 to 2012m11)
** Signficant at 1 per cent
The results indicate that in the first period wages exhibited
convergence whereas in the second period wages exhibited divergence.
β convergence is estimated by regressing the growth rate of wages
over the initial values. The specification of the regression equation takes
the form
Wgi=α+ βWit
where Wgi is the growth rate of wage in state i over the time period
under observation and Wit is the initial wage level in the state. If wages
are converging, then the low wage states should have a faster growth than
high wage states. This would imply a negative relationship between the
initial levels and the growth rates. We have estimated trend growth of
wages in each state for both the periods using a log linear specification
for both the periods. Subsequently, we have regressed the estimated
growth rates over the initial wage levels. The estimated results for both
the period are as:
Wg=0.037**-0.00W2000 (period 2000m7 to 2007m6)
Wg=0.014**+0.00W2007 (period 2000m7 to 2007m6) N=20
The β convergence results presented here do not show evidence of
either convergence or divergence. The limited number of observations
could be a major limitation is estimating β convergence.
Section VIII
Impact of Rising Wages on Cost of Production
In order to understand the inflationary implications of rising wages,
one has to also look at the contribution of wage costs to overall cost of
production. Using the limited data available from the CACP reports,
we have tried to see how the increase in wages would impact the cost
of production. We have computed the share of labour cost in total
operational cost for key food items by taking paddy as representative
item for cereals, tur (arhar) for pulses and groundnut for oilseeds. The
data indicate that labour cost account for a majority of the operational
cost in all the crops (Table 4).
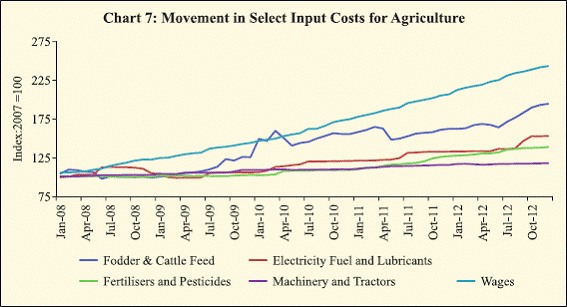
Given that labour cost constitute the most important operational
cost, the increase in cost of production has been dominated by rising
wages. Other costs to production have also gone up significantly in
the recent period. However, a comparative analysis of trends in cost of production in agriculture indicates that the increase in labour cost has
surpassed the increase in cost in the case of most other inputs (Chart 7).
Table 4: Share of Labour Cost in Total Operational Cost during 2010-11 |
Paddy |
Tur (Arhar) |
Groundnut |
States |
Share in % |
States |
Share in % |
States |
Share in % |
Andhra Pradesh |
57.1 |
Andhra Pradesh |
51.5 |
Andhra Pradesh |
51.9 |
Assam |
60.6 |
Bihar |
60.2 |
Gujarat |
29.6 |
Bihar |
60.9 |
Gujarat |
44.2 |
Karnataka |
44.7 |
Chhattisgarh |
45.5 |
Karnataka |
47.5 |
Maharashtra |
43.6 |
Gujarat |
48.4 |
Madhya Pradesh |
51.0 |
Odisha |
58.8 |
Haryana |
54.4 |
Maharashtra |
47.6 |
Tamil Nadu |
54.6 |
Himachal Pradesh |
61.8 |
Odisha |
63.3 |
|
|
Jharkhand |
57.5 |
Tamil Nadu |
61.3 |
|
|
Karnataka |
51.4 |
Uttar Pradesh |
40.1 |
|
|
Kerala |
54.9 |
|
|
|
|
Madhya Pradesh |
49.3 |
|
|
|
|
Maharashtra |
50.1 |
|
|
|
|
Odisha |
64.5 |
|
|
|
|
Punjab |
43.8 |
|
|
|
|
Tamil Nadu |
47.2 |
|
|
|
|
Uttar Pradesh |
48.4 |
|
|
|
|
Uttarakhand |
40.1 |
|
|
|
|
West Bengal |
63.2 |
|
|
|
|
 This increase in cost of production could also feed into the
Minimum Support Prices (MSP). Given that the MSP fixation follows
a cost-plus approach, this could result in significant hikes in MSPs and
as market prices adjust to higher support prices, further increase in food
prices would lead to a spiral. This indicates that the impact of wage
increases on inflation has materialised prominently through the costpush
channel. This is also corroborated by the earlier analysis on wageprice
spiral.
IX. Conclusion
Looking at the recent trends in rural wages, the paper tries to
analyse its implications for inflation. The sharp increases in real wages
since 2007 has led to significant changes in the wage-price dynamics
in the rural area. While in the period prior to 2007, money wages
were responding to changes in prices, in the recent period, prices are
determined by wages. Both high and sustained inflation and institutional
factors like the introduction of MGNREGA could explain some part of
the increase in wages. Apart from this, reduced work force participation
rates in recent period both on account of increased participation in
education and withdrawal of female work force has also contributed to labour market tightening and increase in wages. There has also been
a shift of labour away from agriculture, further contributing to labour
market tightening. State-wise analysis indicates that wages have not
converged in the recent period, despite significant increase in wages.
This could be on account of significant pressure on market wages even
in high wage states. The pressure on inflation from rising wages has
been mostly from the cost-push side, given the dominant contribution
of increasing wage costs to overall cost of production. This calls for
raising agricultural productivity to reduce unit labour costs, so as to
enable a real wage growth environment in a non-inflationary manner.
The present study does not empirically test the impact of MGNREGA
on rural wages. However, given that the MGNREGA wages are indexed
to rural inflation, this could lead to a potential wage-price spiral as the
finding indicates that in the recent period causality runs from wages to
prices. Also, MGNREGA wages were found to be higher than market
wages for most labour supply states indicating that the pressure on
market wages in those states could be significant. However, it is also
recognised that the coverage of MGNREGA has remained relatively
low which could limit the demand pressures. This calls for future work
in terms of exploring the possibility of exploring variations in wages
across states on the dimensions of participation rates in MGNREGA;
the differences in the MGNREGA wage and the market wage as well as
indicators of structural changes in rural labour market.
References
Acharya, S. (1989), “Agriculture Wages in India: A Disaggragated
Analysis”, Indian Journal of Agricultural Economics, Vol. 44, No.2.
Baby, A.A. (1996), Trends in Agricultural Wages in Kerala, Occasional
Paper Series Centre for Development Studies, Trivandrum.
Balakrishnan, Pulapre and M. Parameswaran (2007), “Understanding
Economic Growth in India: A Prerequisite” Economic and Political
Weekly, Vol - 42 No. 27-28, July 14.
Bardhan, P.K. (1970), “The Green Revolution and Agricultural
Laborers”, Economic and Political Weekly, Special Number, July 1970.
Chavan, P. and B. Rajshree (2006), “Trends in Agricultural Wages in
India”, Economic and Political Weekly, Vol. 41, No.38
CACP (2012), “Report of the Commission on Agricutural Costs and
Prices, Khariff, 2012”, Government of India.
Dutta. Puja, Rinku Murgai, Martin Ravallion and Dominique van de
Walle (2012), “Does India‘s Employment Guarantee Scheme Guarantee
Employment?” World Bank Policy Research Working Paper 6003.
Gulati. Ashok, Surbhi Jain and Nidhi Satija (2013) “Rising Farm
Wages in India The ‘Pull’ and ‘Push’ Factors” CACP, Department of
Agriculture and Co-operation, Government of India
Herdt, R.W. and Baker, E.A. (1972), “Agricultural Wages Production
and High Yielding Varieties” Economic and Political Weekly, Vol. 7,
No. 13.
Himanshu (2005), “Wages in Rural India: Sources, Trends and
Comparability”, Indian Journal of Labour Economics, Vol. 48, Number
2, April-June.
Jose A.V. (1974), “Trends in Real Wage Rates of Agricultural Labourers”
Economic and Political Weekly Vol. 9, No. 13.
Jushan Bai and Pierre Perron, (2003). “Computation and analysis of
multiple structural change models,” Journal of Applied Econometrics,
Vol. 18 No 1 pages 1-22.
Krishnaji, N. (1971), “Wages of Agricultural Labourers”, Economic
and Political Weekly Vol. 6, No. 39.
Labour Bureau (2004), Rural Labour Enquiry Report on Employment
and Unemployment of rural Labour Households 1999-2000, Ministry
of Labour Government of India, Shimla.
Lall, D. (1976), “Agricultural Growth: Real Wages and the Rural Poor
in India” Economic and Political Weekly, Vol. 11, No. 26.
Nadhanael, G. V (2005), “Wages and Earnings of Agricultural Labourers
in India: An Inter- State Analysis”, M.Phil Dissertation submitted to
the Jawaharlal Nehru University, Centre for Development Studies,
Thiruvananthapuram (unpublished).
Rao, V.M. (1972), “Agricultural Wages in India: A Reliability Analysis”
Indian Journal of Agricultural Economics. Vol 8, No.2.
Reserve Bank of India (RBI), (2012) “Macroeconomic and Monetary
Developments in India 2011-12”.
Sreedhar,V. (1988) “Agricultural Wages in TamilNadu 1950-51 to 1980-
81”, MPhil Dissertation Submitted to JNU, Centre for Development
Studies, Trivandrum (Unpublished).
Srivastava, R and R. Singh (2005) “Economic Reforms and Agricultural
Wages in India” Indian Journal of Labour Economics Vol. 51. No.3.
Sharma, H.R. (2001), “Employment and Wage Earnings of Agricultural
Labourers: A State wise Analysis” The Indian Journal of Labour
Economics, Vol. 44, No.1.
Annex 1: Co-integration Tests
Period 1: 2000m7 to 2007m6
Series: ALLINDIA_LMW ALLINDIA_LRL |
Unrestricted Cointegration Rank Test (Trace) |
Hypothesized
No. of CE(s) |
Eigenvalue |
Trace
Statistic |
0.05
Critical Value |
Prob.** |
None * |
0.330781 |
36.60037 |
15.49471 |
0.0000 |
At most 1 |
0.033500 |
2.862237 |
3.841466 |
0.0907 |
Unrestricted Cointegration Rank Test (Maximum Eigenvalue) |
Hypothesized
No. of CE(s) |
Eigenvalue |
Max-Eigen
Statistic |
0.05
Critical Value |
Prob.** |
None * |
0.330781 |
33.73814 |
14.26460 |
0.0000 |
At most 1 |
0.033500 |
2.862237 |
3.841466 |
0.0907 |
Both Trace and Max Eigen value tests indicate the presence of one co-integrating vector. |
Sample: 2007M07 2012M11
Series: ALLINDIA_LRL ALLINDIA_LMW
Lags interval (in first differences): 1 to 2 |
Unrestricted Cointegration Rank Test (Trace) |
Hypothesized
No. of CE(s) |
Eigenvalue |
Trace
Statistic |
0.05
Critical Value |
Prob.** |
None * |
0.384033 |
36.26751 |
20.26184 |
0.0001 |
At most 1 |
0.070770 |
4.770943 |
9.164546 |
0.3095 |
Unrestricted Cointegration Rank Test (Maximum Eigenvalue) |
Hypothesized
No. of CE(s) |
Eigenvalue |
Max-Eigen
Statistic |
0.05
Critical Value |
Prob.** |
None * |
0.384033 |
31.49656 |
15.89210 |
0.0001 |
At most 1 |
0.070770 |
4.770943 |
9.164546 |
0.3095 |
Both Trace and Max Eigen value tests indicate the presence of one co-integrating vector. |
Annex 2: VEC Granger Causality/Block Exogeneity Wald Tests
Sample: 2000M07 2007M06 |
Dependent variable: D(ALLINDIA_LMW) |
Excluded |
Chi-sq |
df |
Prob. |
D(ALLINDIA_LRL) |
5.300195 |
2 |
0.0706 |
| All |
5.300195 |
2 |
0.0706 |
Dependent variable: D(ALLINDIA_LRL) |
Excluded |
Chi-sq |
df |
Prob. |
D(ALLINDIA_LMW) |
1.074988 |
2 |
0.5842 |
| All |
1.074988 |
2 |
0.5842 |
Sample: 2007M07 2012M11 |
Dependent variable: D(ALLINDIA_LMW) |
Excluded |
Chi-sq |
df |
Prob. |
D(ALLINDIA_LRL) |
3.556590 |
2 |
0.1689 |
| All |
3.556590 |
2 |
0.1689 |
Dependent variable: D(ALLINDIA_LRL) |
Excluded |
Chi-sq |
df |
Prob. |
D(ALLINDIA_LMW) |
7.320708 |
2 |
0.0257 |
| All |
7.320708 |
2 |
0.0257 |
|